КОНТРОЛЬНАЯ РАБОТА №1

СЕМЕСТР 1

Вариант 1

1. Перемножить матрицы: .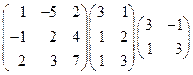

2. Вычислить определители: а) 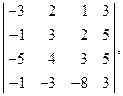б) .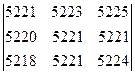

3.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

4. Найти общее решение методом Гаусса

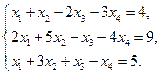
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

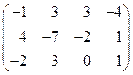6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;–1;1), b = (–1;2;1), c = (1;3;1), d = (–1;–2;3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–b)(3a+4b), б) |(2a–b)´(3a+4b)|,

где |a|=2, |b|=3, a^b=p/6.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(1;3;3), B(–1;2;–2), C(0;–1;3), D(2;1;0).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

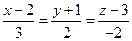и .

10. Построить кривую r = 2sin(2j), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–5;0) и F₂(3;0) есть величина постоянная и равна p=10. Сделать чертеж.

12. Привести уравнение 16x²–9y²–64x–54y–161=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 2

1. Перемножить матрицы: .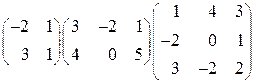

2. Вычислить определители: а) 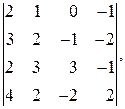б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

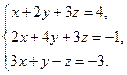
4. Найти общее решение методом Гаусса

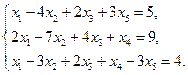
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

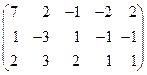6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;4;2), b = (–1;–2;–2), c = (3;5;1), d = (3;5;–1).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (a–3b)(2a+b), б) |(a–3b)´(2a+b)|,

где |a|=4, |b|=2, a^b=2p/3.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(3;2;1), B(1;–2;3), C(0;–1;4), D(2;1;0).

9. Составить каноническое уравнение прямой:

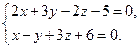
10. Построить кривую r = 2(1+sinj), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–3;0) и F₂(7;0) есть величина постоянная и равна p=6. Сделать чертеж.

12. Привести уравнение 4x²+5y²+24x+30y+61=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 3

1. Перемножить матрицы: .

2. Вычислить определители: а) 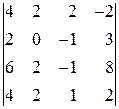б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

4. Найти общее решение методом Гаусса

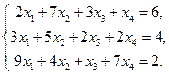
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;2;3), b = (5;1;2), c = (–1;–3;–2), d = (8;0;1).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (a+2b)(b–3a), б) |(a+2b)´(b–3a)|,

где |a|=2, |b|=3, a^b=p/4.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(2;–1;1), B(5;5;4), C(3;2;–1), D(4;1;3).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

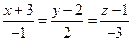и .

10. Построить кривую r = 2(1+sinj), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–4;0) и F₂(2;0) есть величина постоянная и равна p=10. Сделать чертеж.

12. Привести уравнение 5x²–3y²–10x–18y–37=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 4

1. Перемножить матрицы: .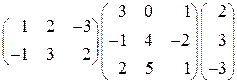

2. Вычислить определители: а) 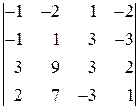б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

4. Найти общее решение методом Гаусса

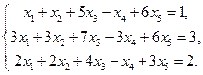
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (1;0;1), b = (0;–2;1), c = (1;3;0), d = (8;9;4).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a+b)(a–3b), б) |(2a+b)´(a–3b)|,

где |a|=3, |b|=4, a^b=p/3.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(2;-1;2), B(1;2;-1), C(3;2;1), D(4;2;3).

9. Составить каноническое уравнение прямой:

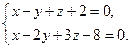
10. Построить кривую r = 2(1+cos2j), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–7;0) и F₂(13;0) есть величина постоянная и равна p=16. Сделать чертеж.

12. Привести уравнение 36x²+49y²+72x–196y–1442=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 5

1. Перемножить матрицы: .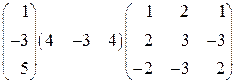

2. Вычислить определители: а) 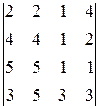б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

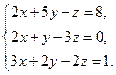
4. Найти общее решение методом Гаусса

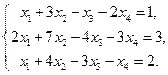
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (1;1;0), b = (–4;3;2), c = (–1;2;1), d = (1;–1;–1).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a+3b)(b–3a), б) |(2a+3b)´(b–3a)|,

где |a|=6, |b|=2, a^b=p/6..

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(2;1;4), B(–1;5;2), C(3;3;2), D(–1;4;3).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

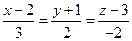и .

10. Построить кривую r = 3(2–cos2j), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–6;0) и F₂(2;0) есть величина постоянная и равна p=10. Сделать чертеж.

12. Привести уравнение 5x²–4y²+30x+8y+21=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 6

1. Перемножить матрицы: .

2. Вычислить определители: а) 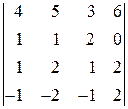б) .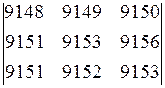

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

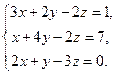
4. Найти общее решение методом Гаусса

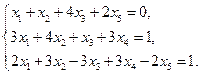
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

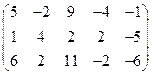6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (5;4;1), b = (–3;5;2), c = (2;–1;3), d = (7;23;4).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–3b)(a–2b), б) |(2a–3b)´(a–2b)|,

где |a|=4, |b|=3, a^b=p/3.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(2;3;1), B(4;1;-2), C(6;3;3), D(5;4;3).

9. Составить каноническое уравнение прямой:

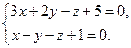
10. Построить кривую r = 3(2–cos2j), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–4;0) и F₂(6;0) есть величина постоянная и равна p=8. Сделать чертеж.

12. Привести уравнение 9x²+16y²+18x–64y–64=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 7

1. Перемножить матрицы: .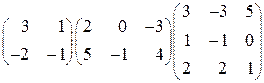

2. Вычислить определители: а) б) .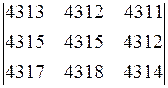

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

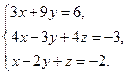
4. Найти общее решение методом Гаусса

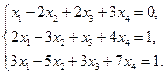
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;1;0), b = (1;0;1), c = (4;2;1), d = (3;1;3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–b)(a+3b), б) |(2a–b)´(a+3b)|,

где |a|=4, |b|=1, a^b=2p/3.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(4;5;–3), B(6;5;–4), C(3;2;0), D(6;3;–3).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

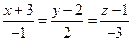и .

10. Построить кривую r = 2sin(4j), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–5;0) и F₂(3;0) есть величина постоянная и равна p=10. Сделать чертеж.

12. Привести уравнение 3x²–5y²+18x+10y+37=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 8

1. Перемножить матрицы: .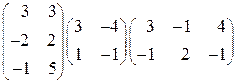

2. Вычислить определители: а) 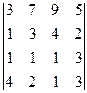б) .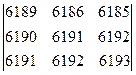

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

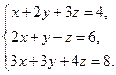
4. Найти общее решение методом Гаусса

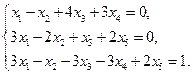
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

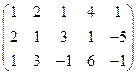6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (3;–1;2), b = (–2;3;1), c = (4;–5;–3), d = (–3;2;–3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (4a–b)(a+2b), б) |(4a–b)´(a+2b)|,

где |a|=3, |b|=2, a^b=p/4.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(1;2;0), B(3;0;3), C(5;2;6), D(4;4;4).

9. Составить каноническое уравнение прямой:

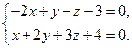
10. Построить кривую r = 2cos(3j), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–11;0) и F₂(9;0) есть величина постоянная и равна p=12. Сделать чертеж.

12. Привести уравнение 4x²+5y²–8x+20y+4=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 9

1. Перемножить матрицы: .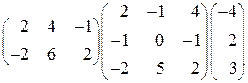

2. Вычислить определители: а) 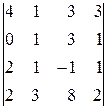б) .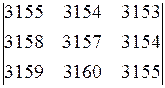

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

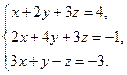
4. Найти общее решение методом Гаусса

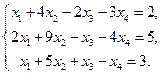
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

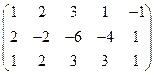6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;2;3), b = (3;1;2), c = (1;3;1), d = (4;0;1).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–3b)(a+2b), б) |(2a–3b)´(a+2b)|,

где |a|=5, |b|=2, a^b=3p/4.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(2;0;4), B(–1;3;-1), C(1;3;–3), D(3;5;0).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

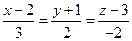и .

10. Построить кривую r = 3cos(4j), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–4;0) и F₂(2;0) есть величина постоянная и равна p=10. Сделать чертеж.

12. Привести уравнение 9x²–4y²–72x–16y+96=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 10

1. Перемножить матрицы: .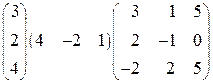

2. Вычислить определители: а) б) .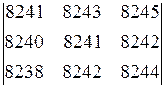

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

4. Найти общее решение методом Гаусса

5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

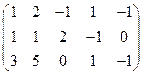6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (–3;1;4), b = (–1;5;4), c = (–1;1;6), d = (0;4;3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (a–4b)(a+2b), б) |(a–4b)´(a+2b)|,

где |a|=3, |b|=2, a^b=5p/6.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(3;1;4), B(–1;5;4), C(1;1;6), D(0;4;3).

9. Составить каноническое уравнение прямой:

10. Построить кривую r = 2sin(4j), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–7;0) и F₂(3;0) есть величина постоянная и равна p=8. Сделать чертеж.

12. Привести уравнение 5x²+9y²+20x+72y+119=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 11

1. Перемножить матрицы: .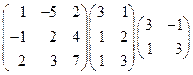

2. Вычислить определители: а) 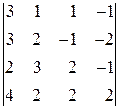б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

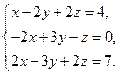
4. Найти общее решение методом Гаусса

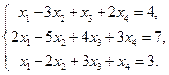
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

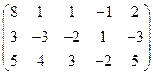6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;–1;1), b = (–1;2;1), c = (1;3;1), d = (–1;–2;3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–b)(3a+4b), б) |(2a–b)´(3a+4b)|,

где |a|=2, |b|=3, a^b=p/6.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если А(–1;–2;0), B(1;1;2), C(1;2;2), D(1;3;3).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

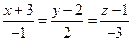и .

10. Построить кривую r = 4sin(2j), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–6;0) и F₂(2;0) есть величина постоянная и равна p=10. Сделать чертеж.

12. Привести уравнение 16x²–9y²–64x–54y–161=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 12

1. Перемножить матрицы: .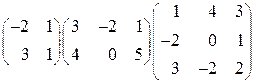

2. Вычислить определители: а) 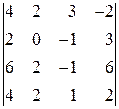б) .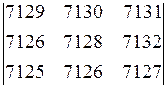

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

4. Найти общее решение методом Гаусса

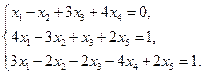
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

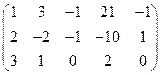6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;4;2), b = (–1;–2;–2), c = (3;5;1), d = (3;5;–1).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–b)(3a+4b), б) |(2a–b)´(3a+4b)|,

где |a|=2, |b|=3, a^b=p/6.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(1;3;–1), B(2;–2;0), C(–1;1;2), D(3;2;1).

9. Составить каноническое уравнение прямой:

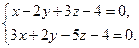
10. Построить кривую 4(2–cosj), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–11;0) и F₂(9;0) есть величина постоянная и равна p=12. Сделать чертеж.

12. Привести уравнение 4x²+5y²+24x+30y+61=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 13

1. Перемножить матрицы: .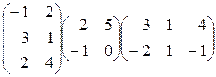

2. Вычислить определители: а) б) .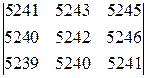

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

4. Найти общее решение методом Гаусса

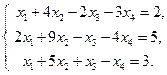
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

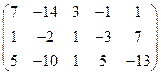6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;2;3), b = (5;1;2), c = (–1;–3;–2), d = (8;0;1).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (a+2b)(b–3a), б) |(a+2b)´(b–3a)|,

где |a|=2, |b|=3, a^b=p/4.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(2;3;4), B(–2;0;3), C(–1;2;1), D(2;–1;1).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

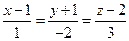и .

10. Построить кривую r = 5(2–sinj), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–7;0) и F₂(5;0) есть величина постоянная и равна p=20. Сделать чертеж.

12. Привести уравнение 3x²–5y²+18x+10y+37=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 14

1. Перемножить матрицы: .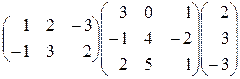

2. Вычислить определители: а) 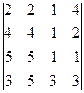б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

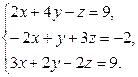
4. Найти общее решение методом Гаусса

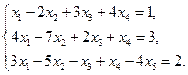
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (1;0;1), b = (0;–2;1), c = (1;3;0), d = (8;9;4).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a+b)(a–3b), б) |(2a+b)´(a–3b)|,

где |a|=3, |b|=4, a^b=p/3.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(4;–1;2), B(2;2;–2), C(3;0;1), D(2;1;2).

9. Составить каноническое уравнение прямой:

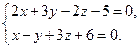
10. Построить кривую r = 4(2–cosj), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–3;0) и F₂(7;0) есть величина постоянная и равна p=6. Сделать чертеж.

12. Привести уравнение 36x²+49y²+72x–196y–1442=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 15

1. Перемножить матрицы: .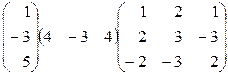

2. Вычислить определители: а) 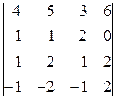б) .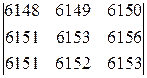

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

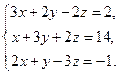
4. Найти общее решение методом Гаусса

5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

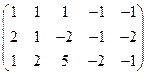6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (1;1;0), b = (–4;3;2), c = (–1;2;1), d = (1;–1;–1).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a+3b)(b–3a), б) |(2a+3b)´(b–3a)|,

где |a|=6, |b|=2, a^b=p/6.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(–3;–2;2), B(1;1;3), C(2;1;–1), D(2;1;4).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

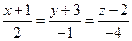и .

10. Построить кривую r = 2(1+cos2j), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–4;0) и F₂(8;0) есть величина постоянная и равна p=20. Сделать чертеж.

12. Привести уравнение 9x²–4y²–72x–16y+96=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 16

1. Перемножить матрицы: .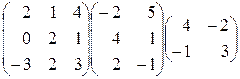

2. Вычислить определители: а) 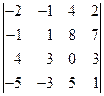б) .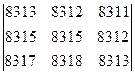

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

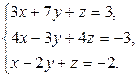
4. Найти общее решение методом Гаусса

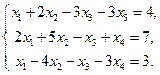
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

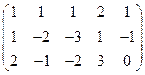6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (1;1;0), b = (–3;5;2), c = (2;–1;3), d = (7;23;4).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–3b)(a–2b), б) |(2a–3b)´(a–2b)|,

где |a|=4, |b|=3, a^b=p/3.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(5;–1;3), B(4;1;2), C(3;2;1), D(5;2;4).

9. Составить каноническое уравнение прямой:

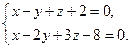
10. Построить кривую sin²(2j), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–7;0) и F₂(13;0) есть величина постоянная и равна p=16. Сделать чертеж.

12. Привести уравнение 9x²+16y²+18x–64y–64=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 17

1. Перемножить матрицы: .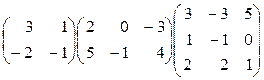

2. Вычислить определители: а) 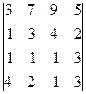б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

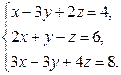
4. Найти общее решение методом Гаусса

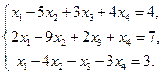
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

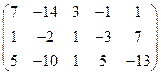6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если = (2;1;0), b = (1;0;1), c = (4;2;1), d = (3;1;3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–3b)(a–2b), б) |(2a–3b)´(a–2b)|,

где |a|=4, |b|=3, a^b=p/3.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(5;–1;0), B(2;2;–1), C(3;1;–2), D(4;5;1).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

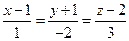и .

10. Построить кривую r = 2cos(3j), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–7;0) и F₂(5;0) есть величина постоянная и равна p=20. Сделать чертеж.

12. Привести уравнение 16x²–9y²–64x–54y–161=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 18

1. Перемножить матрицы: .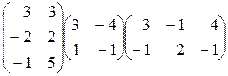

2. Вычислить определители: а) б) .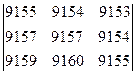

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

4. Найти общее решение методом Гаусса

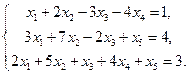
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (3;–1;2), b = (–2;3;1), c = (4;–5;–3), d = (–3;2;–3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (4a–b)´(a+2b), б) |(4a–b)´(a+2b)|,

где |a|=3, |b|=2, a^b=p/4.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(3;–3;0), B(–1;1;2), C(2;1;1), D(4;0;2).

9. Составить каноническое уравнение прямой:

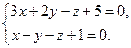
10. Построить кривую r = 6sin(3j), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–4;0) и F₂(6;0) есть величина постоянная и равна p=8. Сделать чертеж.

12. Привести уравнение 4x²+5y²–8x+20y+4=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 19

1. Перемножить матрицы: .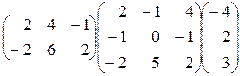

2. Вычислить определители: а) 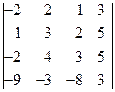б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

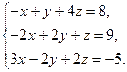
4. Найти общее решение методом Гаусса

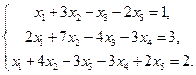
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

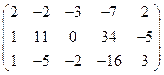6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;2;3), b = (3;1;2), c = (1;3;1), d = (4;0;1).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–3b)(a+2b), б) |(2a–3b)´(a+2b)|,

где |a|=5, |b|=2, a^b=3p/4.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(1;2;–3), B(2;–1;1), C(1;3;–2), D(3;1;2).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

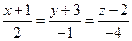и .

10. Построить кривую r = 4(1–cosj), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–7;0) и F₂(5;0) есть величина постоянная и равна p=20. Сделать чертеж.

12. Привести уравнение 5x²–3y²–10x–18y–37=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 20

1. Перемножить матрицы: .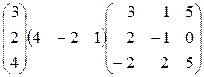

2. Вычислить определители: а) б) .

2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

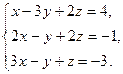
4. Найти общее решение методом Гаусса

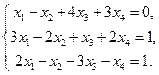
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

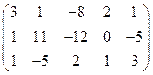6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (–3;1;4), b = (–1;5;4), c = (–1;1;6), d = (0;4;3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (a–4b)(a+2b), б) |(a–4b)´(a+2b)|,

где |a|=3, |b|=2, a^b=5p/6.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(4;4;5), B(2;3;4), C(1;2;2), D(3;1;3).

9. Составить каноническое уравнение прямой:

10. Построить кривую r = 5(1–sinj), заданную в полярных координатах.

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F₁(–11;0) и F₂(9;0) есть величина постоянная и равна p=12. Сделать чертеж.

12. Привести уравнение 5x²+9y²+20x+72y+119=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 21

1. Перемножить матрицы: .

2. Вычислить определители: а) 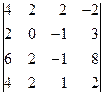б) .

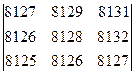2.Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.

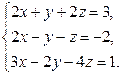
4. Найти общее решение методом Гаусса

5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

.

6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;–1;1), b = (–1;2;1), c = (1;3;1), d = (–1;–2;3).

7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:

а) (2a–b)(3a+4b), б) |(2a–b)´(3a+4b)|,

где |a|=2, |b|=3, a^b=p/6.

8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если А(–1;–2;0), B(1;1;2), C(1;2;2), D(1;3;3).

9. Составить уравнение плоскости, проходящей через две параллельные прямые:

и .

10. Построить кривую r = 2(1–sinj), заданную в полярных координатах.

11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F₁(–4;0) и F₂(2;0) есть величина постоянная и равна p=10. Сделать чертеж.

12. Привести уравнение 5x²–3y²–10x–18y–37=0 к каноническому виду, определить тип кривой и сделать чертеж.

Вариант 22

1. Перемножить матрицы: .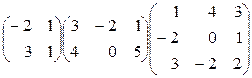

2. Вычислить определители: а)