ДЕДУКЦИЯ И ИНДУКЦИЯ В УЧЕБНОМ ПРОЦЕССЕ

Как в любом процессе мышления (научного или обыденного), так и в процессе обучения дедукция и индукция взаимосвязаны. «Индукция и дедукция связаны между собой столь же необ­ходимым образом, как синтез и анализ. Вместо того чтобы односторонне превозносить одну из них до небес за счет другой, надо стараться применять каждую на своем месте, а этого можно добиться лишь в том случае, если не упускать из виду их связь между собой, их взаимное дополнение друг друга»⁷.В индукции мы идем от посылок, выражающих знания меньшей степени общности, к новому суждению большей степени общности, от отдельных конкретных явлений к обобщению. В дедукдии ход рассуждения противоположный, т. е. от обобщений, выводов мы идем к отдельным конкретным фактам или суждениям меньшей степени общности.

В процессе обучения индуктивный и дедуктивный методы используются в единстве. Индуктивный метод используется тог­да, когда изучается новый материал, трудный для учащихся, и когда в результате беседы они смогут сделать сами определен­ное заключение, обобщение, сформулировать правило, теорему или некоторую закономерность. Индуктивный метод в большей мере активизирует учащихся, однако требует от учителя творчес­кого подхода и гибкости в преподавании. При этом затрачивает­ся больше времени на подведение учащихся к самостоятельному заключению.

Дедуктивный метод состоит в том, что учитель сам фор­мулирует общее суждение, выражающее какое-то правило, закон, теорему и т. д., а затем применяет его, иллюстрирует частными примерами, случаями, фактами, событиями и т. д. Соединение дедукции и индукции в процессе обучения дает два пути объясне­ния материала: «Индуктивно-дедуктивный путь объяснения материала, когда последнее начинается с индукции и переходит затем в дедукцию (возможно, при значительном перевесе индук­ции), и путь дедуктивно-индуктивный, когда сообщение уча­щимся нового осуществляется самим учителем в виде готового, сформулированного им правила или положения с последующими комментариями»⁸.

К. Д, Ушинский высоко ценил применение индукции при изучении грамматики. На специально подобранных примерах он развивал у детей умение подмечать закономерности языка и де­лать самостоятельные обобщения, формулировать правила, что имело огромное значение для развития мышления младших школьников. Дедукцию Ушинский ценил не меньше индукции и большую роль в обучении языку отводил последующим упра­жнениям, направленным на подыскание самими учащимися при­меров на только что сформулированное правило. Известный советский методист А. В. Текучев, обобщив данные эксперимен­тальной проверки применения этих двух способов изучения мате­риала, сделал вывод о том, что в работе над темой «Однородные члены предложения» (общее понятие, союзы при однородных членах, обобщающие слова) с одинаковым успехом могут быть использованы оба пути; изучение же правил постановки знаков препинания при однородных членах предпочтительнее проводить дедуктивно-индуктивным способом⁹. Эти же приемы использу­ются не только на уроках родного языка, но и на уроках матема­тики, истории, физики и др. Соответствующая методика преподавания школьного предмета рекомендует учителям более конкретное использование этих методов в работе над отдельными темами учебной программы.

В математике имеется много приверженцев как индуктивного, гак и дедуктивного метода. Например, Л. Д. Кудрявцев полага­ет, что «на первых этапах обучения надо отдавать предпочтение индуктивному методу, постепенно подготавливая и используя дедуктивный подход»¹⁰, ибо индуктивные методы изложения материала, при которых происходит последовательное обобще­ние понятий, способствуют более активному усвоению материа­ла. Далее он отмечает: «В последние годы наблюдается стремле­ние заменять по возможности индуктивный подход дедуктивным, целесообразность этого часто представляется сомнительной»¹¹.

Однако как при индуктивном, так и при дедуктивном методе при изложении новых понятий или новых общих теорий необ­ходимо отводить значительное время на конкретные иллюст­рации, на разбор примеров, анализ частных ситуаций. От самого учителя зависит оптимальный выбор методов, позволяющий на высоком уровне самостоятельности организовать познаватель­ную деятельность учащихся.

В математике используются различные виды индукции: пол­ная, неполная и математическая. Применение математической индукции покажем на следующем примере. Надо определить сумму л первых нечетных чисел:

1+3 + 5 + 7 + ... + (2n-1)¹².

Обозначив эту сумму через S (n), положим n = 1, 2, 3, 4, 5; тогда будем иметь:

S(1)=1,

S (2)= 1+3=4,

S (3)=1+3 + 5 = 9,

S (4)=1+3 + 5 + 7 = 16,

S (5)=1 + 3 + 5+ 7 + 9=25.

Мы наблюдаем интересную закономерность: при n = 1, 2, 3, 4, 5 сумма л последовательных нечетных чисел равна n². Но заклю­чение по аналогии, что это имеет место при любом л, сделать нельзя, ибо оно может оказаться ошибочным. Применим метод математической индукции, т. е. предположим, что для какого-то числа л наша формула верна, и попытаемся доказать, что Тогда она верна и для следующего числа n +1. Итак, мы полагаем, что S(n)-1 + 3 + 5 + ... + (2n-1)=n². Вычислим S(n+1)=1+3 + 4+ 5 + ... +(2n- 1) + (2n +1). Но по предположению сумма n первых слагаемых равна л², следовательно, S(n+1) = n² + (2n + 1) = (n+1)².Итак, предположив, что S(n) — n², мы доказали, чтo S (n+ 1) = (n +1)². Но мы выше проверили, что эта формула верна для n = 1, 2, 3, 4, 5, следовательно, она будет верна и для n=6₎ и для n=7 и т. д. Формула считается доказанной для любого числа слагаемых.

Этим же методом доказывается, что сумма n первых натура­льных чисел, обозначенная S₁ (n), равна т. е.

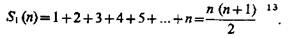
В математическом мышлении присутствуют не только логи­ческие рассуждения, но и математическая интуиция, фантазия и чувство гармонии, позволяющие предвидеть ход решения зада­чи или доказательства теоремы. Однако в математике, пишет Л. Д. Кудрявцев, «интуитивные соображения и правдоподобные рассуждения отдаются на суд холодного рассудка для их изучения, доказательства или опровержения». Истинность суждения там доказывается «не проверкой его на ряде примеров, не прове­дением ряда экспериментов, что не имеет для математики до­казательной силы, а чисто логическим путем, по законам фор­мальной логики»¹⁴. В ходе обучения математике предполагается, что «использование знаний, математического аппарата, интуи­ции, чувства гармонии, фантазии, умения думать, логики, экс­перимента происходит не последовательно по этапам — все это взаимодействует между собой в течение всего процесса...»¹⁵. В результате этого взаимодействия у учащихся вузов и средних учебных заведений формируется, воспитывается математическая культура. Итак, единство дедукции и индукции в обучении и в на­учном творчестве своеобразно и ярко проявляется в математи­ке — науке, значительно отличающейся от естественных и от общественных наук как по методам доказательства, так и по методике передачи знаний учащимся.

Выше мы приводили типы и примеры сокращенных умозак­лючений (категорического силлогизма, условных, разделитель­ных и др.).

В ходе обучения математике учащиеся приобретают способ­ность к свертыванию процесса математического рассуждения при решении задач знакомого типа — об этом писали еще известные русские методисты С. И. Шохо-Троцкий (в 1916 г.) и Ф. А. Эрн (в 1915 г.). Они отмечали, что «при многократном решении однотипных задач учащимися отдельные этапы мыслительного процесса сокращаются и перестают осознаваться, но когда нуж­но, учащийся может вернуться к полному развернутому рассуж­дению»¹⁶. Методисты-математики П. А. Шеварев и Н. А. Менчинская в начале 40-х годов также установили соответственно на алгебраическом и арифметическом материале, что «наряду с развернутыми умозаключениями в умственной деятельности школьников при решении задач занимают определенное место и сверну­тые умозаключения, когда ученик не осознает правила общего положения, в соответствии с которыми он фактически действу­ет... не выполняет всей той цепи соображений и умозаключений, которые образуют полную, развернутую систему решения»¹⁷. Сокращение процесса рассуждения возникает благодаря упра­жнениям, причем способные к математике учащиеся переходят к свернутым рассуждениям быстро, средние — медленнее, у не­способных же не замечалось сколько-нибудь заметного свертыва­ния даже в результате многих упражнений. В. А. Крутецкий высказывает такую гипотезу: «Вообще никогда и нигде, вероят­но, человек не мыслит до конца развернутыми структурами»¹⁸. Однако способные ученики мыслят свернутыми структурами, сокращенными умозаключениями при решении не только одно­типных, но и новых задач; при этом по просьбе экспериментатора эти учащиеся восстанавливали свернутые структуры до полной (с их точки зрения) структуры. «Свернутые» мыслительные струк­туры способствуют более быстрой переработке информации, ускорению процесса решения задач, упрощают выполнение сложных операций.

Изучая компоненты структуры математических способностей школьников, В. А. Крутецкий проанализировал высказывания ряда ученых-математиков и преподавателей математики средних школ по этому вопросу. Приблизительно 38% опрошенных това­рищей обратили внимание на свертывание процесса рассуждения у способных учащихся. Приведем эти высказывания. «Процесс рассуждения у способных учащихся сокращен и никогда не раз­вернут до полной логической структуры. Это очень экономно, и в этом его значение»; «Я часто наблюдал, как мыслят способ­ные ученики, — для учителя и класса это развернутый и последо­вательный во всех звеньях процесс, а для себя — это отрывоч­ный, беглый, сокращенный, прямо стенограмма мысли»¹⁹.

Перечисляя качества ума этих учащихся, почти все опрошен­ные учителя математики и математики-ученые (98%) отмечали способность к обобщению. «Способный ученик быстро обобщает не только математический материал, но и метод рассуждения, доказательства»; некоторые из опрошенных указывали на спосо­бность и даже своеобразную «страсть» к обобщению, способ­ность «видеть общее в разных явлениях», «способность прийти от частного к общему»²⁰.

Если проанализировать знания, умения и навыки учащихся, относящиеся к использованию дедукции и индукции в процессе обучения по дисциплинам нематематического профиля, то наря­ду с положительными моментами можно выделить и ряд недо­статков. Прежде всего недостаточно развито умение использовать дедуктивный ход рассуждений: дав верное определение учащийся не всегда справляется с анализом конкретного произведения под углом зрения этого определения, у некоторых yчащихся отсутствуют выводы по теме сочинения, в сознании учащихся иногда имеет место разрыв между фактологическими и те­оретическими знаниями и т. д.

Отмеченные положительные моменты и недостатки в знаниях учащихся свидетельствуют о важном значении умелого сочетания индукции и дедукции в ходе изложения, закрепления и проверки усвоения школьного материала. Общих рецептов по поводу того, как, в какой мере использовать дедуктивный или индуктивные метод в обучении, дать нельзя. В связи с этим можно отметить высказывание Л. Д. Кудрявцева о методических принципах пре­подавания математики: «К сожалению, не существует точных рецептов, как надо преподавать различные разделы математики. Методика преподавания математики не наука, а искусство, Правда, это вовсе не означает, что методике преподавания мате­матики не надо учить. Всякому искусству можно и должно учить: учатся и художники, и музыканты, и артисты, и писатели».

На основе разбора ошибок, допускаемых в педагогическом процессе, можно еще раз сделать вывод о творческом характере применения различных методов обучения и воспитания, о недо­пустимости шаблонного подхода в процессе обучения.