Графический метод кинематического анализа

КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ

Цели и задачи кинематического анализа

Синтез механизма – проектирование – имеет значительные трудности теоретического характера, поэтому при выполнении прикладных инженерных задач менее распространен, чем анализ.

Анализ механизма – исследование его основных параметров с целью изучения законов изменения и на основе этого выбор из ряда известных наилучшего механизма. По сравнению с синтезом анализ механизма широко используется в практике.

Цели:

1. Определение кинематических характеристик звеньев: перемещение; скорость; ускорение; траектория движения; функция положения при известных законах движения входных (ведущих) звеньев.

2. Оценка кинематических условий работы рабочего (выходного) звена.

3. Определение необходимых численных данных для проведения силового, динамического, энергетического и других расчётов механизма.

Задачи:

о положениях звеньев механизма. Определение траекторий движения точек;

о скоростях звеньев или отдельных точек механизма;

об ускорениях звеньев или отдельных точек механизма.

Методы:

графический (или метод графиков и диаграмм);

графоаналитический (или метод планов скоростей и ускорений);

аналитический;

экспериментальный.

Графический метод кинематического анализа

Преимущество этого метода заключается в наглядности и простоте. Он хорош для кинематического анализа звеньев, совершающих возвратно-поступательное движение. Недостаток метода – невысокая точность, которая зависит от точности графических построений.

Задача о положениях решается построением нескольких совмещённых планов механизма в выбранном масштабе длин при различных последовательных положениях ведущего звена.

Задачи о скоростях и ускорениях решаются построением графиков (диаграмм) перемещений, скоростей и ускорений исследуемой точки.

Последовательность кинематического анализа:

1. Сначала строят несколько (чаще всего 12 и более) совмёщенных планов механизма в произвольно выбранном масштабе длин.

2. Затем строят график пути (перемещения) исследуемой точки или звена, для чего используют совмещённые планы механизма и последовательные положения на них исследуемой точки или звена.

3. Графическим дифференцированием графика перемещений строят график скорости исследуемой точки.

4. Графическим дифференцированием графика скоростей строят график ускорений.

Графическое дифференцирование можно производить методом хорд и методом касательных. С целью повышения точности удобно использовать оба метода одновременно.

Пример

Даны кривошипно-ползунный механизм, длины звеньев которого – кривошипа и шатуна – L_OA и L_AB соответственно, и угловая скорость кривошипа w₁ = const.

Определитьскорости и ускорения ползуна при различных положениях кривошипа.

Решение

Выбираем масштабы длин 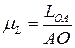, м/мм, где AO – длина отрезка, мм, изображающая кривошип длиной L_ОА на строящемся плане механизма; эта длина выбирается произвольно с учётом того, что совмещённые планы механизма должны разместиться на отведённом месте чертежа, а сам масштаб длин был бы удобен для дальнейших расчётов.

Вычисляем длину отрезка , мм, изображающего шатун на плане механизма. При построении совмещенных планов механизма используют метод засечек (рис. 2.1).

Для построения графиков скоростей и ускорений (рис. 2.1) выбираются полюсные расстояния h_u и h_a, где h_u – полюсное расстояние при построении графика скоростей, которое выбирается произвольной длины; рекомендуется его величину выбирать в пределах h_u » 30…40 мм; h_a – полюсное расстояние при построении графика ускорений; его рекомендуется принимать в пределах h_a »30…40 мм.

Масштабы времени, скорости и ускорения вычисляют по формулам, вывод которых приводится ниже.

Масштаб времени можно вычислить по формуле

,

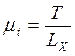где Т – период одного оборота кривошипа, с; L_X – длина отрезка между точками 1 и 1 на графике (диаграмме) перемещений, мм.

Так как период Т можно вычислить по формулам

, или , с,

где ω₁ – угловая скорость кривошипа, 1/с; n₁ – частота вращения кривошипа, об/мин, то масштаб времени

, с/мм.

Масштаб скорости можно вывести из условия, что скорость исследуемой точки является производной перемещения S по времени:

.

Здесь предполагается, что масштаб перемещений μ_s и масштаб времени μ_t являются постоянными величинами.

Так как , то , отсюда

, .

Масштаб ускорения, вывод которого аналогичен предыдущему, вычисляется по формуле

, .

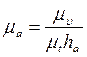Для определения величины скорости или ускорения в каком-либо положении точки В необходимо длину ординаты соответствующего графика умножить на масштаб m_u или m_a соответственно.

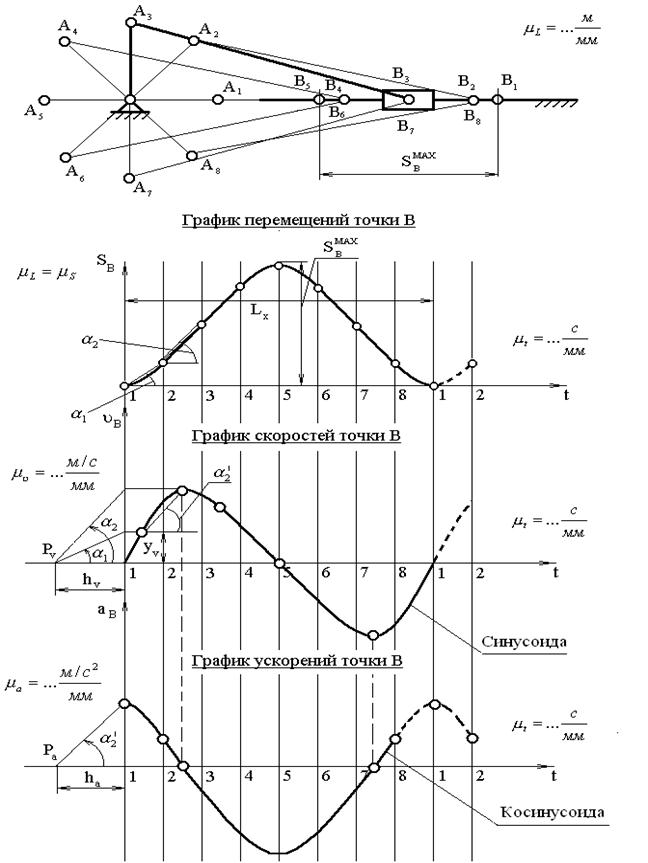
Рис. 2.1. Совмещённые планы механизма,

графики перемещений, скоростей и ускорений