
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Криволинейное движение
При поступательном движении тела все его точки описывают одинаковые траектории и в любой момент времени имеют равные по модулю и параллельно направленные скорости и ускорения.
Криволинейное движение
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.
Частным случаем криволинейного движения – является движение по окружности.
20. Вращательным движением твердого тела вокруг неподвижнойосиназывается такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными.
Скорости и ускорения точек тела при вращении.
Перейдем к изучению движения отдельных точек твердого тела. Известно уравнение вращения твердого тела вокруг неподвижной оси  .
.
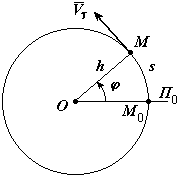 Рассмотрим какою-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения. При вращении твердого тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр О лежит на самой оси. Если за время
Рассмотрим какою-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения. При вращении твердого тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр О лежит на самой оси. Если за время  происходит элементарный поворот тела на угол
происходит элементарный поворот тела на угол  , то точка М при этом совершает вдоль своей траектории элементарное перемещение
, то точка М при этом совершает вдоль своей траектории элементарное перемещение  .
.
Тогда алгебраическая скорость будет равна
 или
или 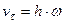 (5-1)
(5-1)
Рис. 5-1
Скорость точки равна  . Скорость
. Скорость  в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью.
в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью.
Модуль скорости равен
 . (5-2)
. (5-2)
Величины скоростей точек тела, при его вращении вокруг неподвижной оси, пропорциональны кратчайшим расстояниям от этих точек до оси. Коэффициентом пропорциональности является угловая скорость  . Скорости точек направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.
. Скорости точек направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.
Ускорение точки раскладываем на касательную и нормальную составляющие, т.е.
 .
.
Касательное и нормальное ускорения вычисляются по формулам
 ,
,  .
.
Таким образом  ,
,  и модуль ускорения вычисляется по формуле
и модуль ускорения вычисляется по формуле  .
.
Касательные, нормальные и полные ускорения точек тела, при его вращении вокруг неподвижной оси, как и скорости, так же пропорциональны кратчайшим расстояниям от этих точек до оси. Нормальное ускорение направлено по радиусу окружности к оси вращения. Направление касательного ускорения зависит от знака углового ускорения.
Скорость точки по модулю и направлению можно представить векторным произведением
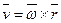 ,
,
где  - радиус-вектор точки М, проведенный из произвольной точки оси вращения
- радиус-вектор точки М, проведенный из произвольной точки оси вращения  .
.
Это выражение называется векторной формулой Эйлера.
Угловая скорость:
 или
или 
Угловое ускорение:
 или
или 
21. Ускорение точки раскладываем на касательную и нормальную составляющие, т.е.
 .
.
Касательное и нормальное ускорения вычисляются по формулам
 ,
,  .
.
22. -
27. Методы нахождения положения МЦС
1). Известен вектор скорости  какой -либо точки A плоской фигуры и ее угловая скорость какой -либо точки A плоской фигуры и ее угловая скорость  . .
| 
|
МЦС (точка P) находится на перпендикуляре к вектору  , проведенном через точку A. Расстояние , проведенном через точку A. Расстояние  и откладывается в сторону, которую указывает вектор и откладывается в сторону, которую указывает вектор  после поворота на угол после поворота на угол  в направлении дуговой стрелки в направлении дуговой стрелки  . При этом получается, что скорость . При этом получается, что скорость
 ( (  ) )
| |
2). Известны не параллельные друг другу скорости  и и 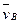 двух точек плоской фигуры. двух точек плоской фигуры.
| 
|
МЦС (точка P) находится в точке пересечения перпендикуляров, проведенных через точки A и B к скоростям этих точек. Угловая скорость плоской фигуры равна 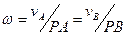 . Отметим, что для нахождения только положения МЦС достаточно знать лишь направления скоростей двух точек . . Отметим, что для нахождения только положения МЦС достаточно знать лишь направления скоростей двух точек .
| |
3). Известны параллельные друг другу скорости  и и 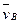 точек A и B плоской фигуры, перпендикулярные отрезку AB, направленные в одну сторону и не равные по модулю ( точек A и B плоской фигуры, перпендикулярные отрезку AB, направленные в одну сторону и не равные по модулю (  ). ).
| 
|
МЦС (точка P) находится в точке пересечения продолжения отрезка AB и прямой, проведенной через концы векторов  и и 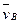 . При заданной длине отрезка AB расстояния от МЦС до точек A и B определяются из пропорции . При заданной длине отрезка AB расстояния от МЦС до точек A и B определяются из пропорции 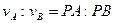 . Угловая скорость фигуры . Угловая скорость фигуры 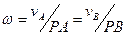 . Случай равенства ( . Случай равенства ( 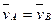 ) см. п. 6. ) см. п. 6.
|
Дата добавления: 2015-04-15; просмотров: 370; Мы поможем в написании вашей работы!; Нарушение авторских прав |