Модуль векторного произведения: .

Условие равновесия пар сил: Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов .

Момент силы относительно точки – вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся повернуться против хода часовой стрелки. Плечо "h"– кратчайшее расстояние от точки до линии действия силы.

Момент силы равен векторному произведению вектора на вектор .

Модуль векторного произведения: .

В динамике поступательного движения материальной точки были введены в дополнение к кинематическим величинам, понятия силы и массы. Аналогично, для изучения динамики вращательного движения тела, помимо рассмотренных кинематических характеристик, вводятся новые величины - момент силы, момент инерции и момент импульса.

момент силы

.

С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора , проведенного в точку приложения силы на эту силу. Таким образом, момент силы относительно точки О является векторной величиной и равен

Рис. 7.1. К определению момента импульса частицы.

Момент импульса частицы. Моментом импульса L частицы A относительно точки О называется величина, равная векторному произведению радиус-вектора частицы на ее импульс p: L = [r·p] = [r·mv]. (7.1) В общем случае произвольного движения относительно точки О модуль момента импульса частицы равен: L = r·m·v·sin() = R·m·v, где R - плечо импульса частицы относительно точки О (см. рис. 7.1).

Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы и , и образует с ними правую тройку векторов (при наблюдении из вершины вектора М видно, что вращение по кратчайшему расстоянию от к происходит против часовой стрелки).

Момент импульса твердого тела. Рассмотрим твердое тело, совершающее вращательное движение вокруг некоторой оси со скоростью w. Моментом импульса тела называется величина, равная векторной сумме моментов импульса его частей:

L = L_i = [r_i·p_i] = [r_i·m_iv_i]. (7.1_.)

В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами , и моменты инерции тела определяется интегралом

о где 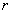- расстояние от элемента до оси вращения

Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс известен. Необходимо определить момент инерции относительно произвольно оси 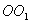параллельной оси . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:

Динамика вращательного движения материальной точки. Рассмотрим частицу массы m, вращающуюся вокруг токи О по окружности радиуса R, под действием результирующей силы F (см. рис. 8.5). В инерциальной системе отсчета справедлив 2^ой закон Ньютона. Запишем его применительно к произвольному моменту времени:

F = m·a.

Нормальная составляющая силы не способна вызвать вращения тела, поэтому рассмотрим только действие ее тангенциальной составляющей. В проекции на тангенциальное направление уравнение движения примет вид:

F_= m·a_.

Поскольку a_= ·R, то

F_= m··R_(8.6)

Умножив левую и правую части уравнения скалярно на R, получим:

F_·R= m··R² (8.7)
M = I· (8.8)

8 Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью , то линейная скорость i-ой точки равна , где , - расстояние от этой точки до оси вращения. Следовательно.

где - момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

где - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.