Основные законы электрических цепей

На рис. 1.7 изображен участок цепи с сопротивлением R. Ток, протекающий через сопротивление R, пропорционален падению напряжения на сопротивлении и обратно пропорционален величине этого сопротивления. Это закон Ома.

Падение напряжения на сопротивлении- это произведение тока, протекающего через сопротивление, на величину этого сопротивления.

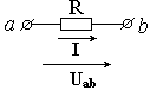
Рис. 1.7

Основными законами электрических цепей, наряду с законом Ома, являются закон баланса токов в узлах (первый закон Кирхгофа) и закон баланса напряжений на замкнутых участках (второй закон Кирхгофа). В соответствии с первым законом Кирхгофа, алгебраическая сумма токов в любом узле цепи равна нулю:

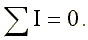
Возьмем схему на рис. 1.8 и запишем для нее уравнение по первому закону Кирхгофа.

Токам, направленным к узлу, присвоим знак "плюс", а токам, направленным от узла - знак "минус". Получим следующее уравнение:

Рис. 1.8

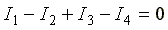или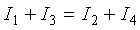

Согласно второму закону Кирхгофа, алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжений в этом контуре

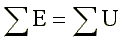
Возьмем схему на рис. 1.9 и запишем для внешнего контура этой схемы уравнение по второму закону Кирхгофа.

Для этого выберем произвольно направление обхода контура, например, по часовой стрелке. ЭДС и падения напряжений записываются в левую и правую части уравнения со знаком "плюс", если направления их совпадают с направлением обхода контура, и со знаком "минус", если не совпадают.
При определении тока в ветви, содержащей источник ЭДС, используют закон Ома для активной ветви.

Рис. 1.9

Возьмем ветвь, содержащую сопротивления и источники ЭДС. Ветвь включена к узлам a-b, известно направление тока в ветви (рис. 1.10).

Возьмем замкнутый контур, состоящий из активной ветви и стрелки напряжения Uab, и запишем для него уравнение по второму закону Кирхгофа. Выберем направление обхода контура по часовой стрелке.

Рис.1.10

Получим

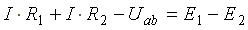
Из этого уравнения выведем формулу для тока

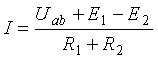
В общем виде:

,

где Σ R - сумма сопротивлений ветви;
Σ E - алгебраическая сумма ЭДС.

ЭДС в формуле записывается со знаком "плюс", если направление ее совпадает с направлением тока и со знаком "минус", если не совпадает.