Нахождение токов в ветвях.

Токи в ветвях находятся по закону Ома:

I₁ = U / Z₁, ψ_i1 = ψ_u + φ₁, I₂ = U / Z₂, ψ_i2 = ψ_u + φ₂.

Нахождение тока всей цепи.

Ток всей цепи может быть найден несколькими методами: графическим, методом мощностей, методом проекций и методом проводимостей.

Чаще всего используют метод проекций и метод проводимостей. В методе проекций ток I₁ и I₂ раскладываются по две ортогональные составляющие активную и реактивную. Ось активной составляющей совпадает с вектором напряжения U. Ось реактивной составляющей перпендикулярна вектору U (рис. 35).

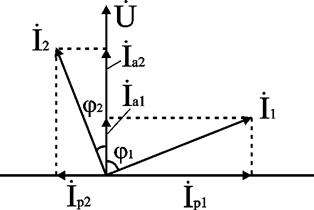
Рис. 35 Ось реактивной составляющей

Активные составляющие токов равны:

(2.18)

I_1а = I₁ cos φ₁, I_2а = I₂ cos φ₂,

(2.19)

I_а = I_1а + I_2а.

Реактивные составляющие токов равны:

(2.20)

I_1р = I₁ sin φ₁, I_2р = I₂ sin φ₂,

(2.21)

I_р = I_1р - I_2р.

В последнем уравнении взят знак минус, поскольку составляющие I_1р (индуктивная) и I_2р (емкостная) направлены в разные стороны от оси U.

Полный ток находится из уравнений:

(2.22)

,

(2.23)

φ = arctg(I_р / I_а).

В методе проводимостей также используется разложение на активные и реактивные составляющие. Активные составляющие токов записываются в виде:

(2.24)

,

где через g₁ = R₁ / Z₁² обозначена величина названная активной проводимостью первой ветви. Аналогичным образом получим:

(2.25)

,

где g₂ = R₂ / Z₂²; а величину g = g₁ + g₂ называют активной проводимостью всей цепи.

Запишем реактивные составляющие токов:

(2.26)

,

(2.27)

,

где b₁ и b₂ – реактивные проводимости ветвей b₁ = X_L / Z₁², b₂ = X_C / Z₂². Для реактивной проводимости всей цепи имеем:

(2.28)

b = b₁ - b₂.