Емкость

Все проводники с электрическим зарядом создают электрическое поле. Характеристикой этого поля является разность потенциалов (напряжение). Электрическую емкость определяют отношением заряда проводника к напряжению

C = Q / U_C.

С учетом соотношения

i = dQ / dt

получаем формулу связи тока с напряжением

i = C · du_C / dt.

Для удобства ее интегрируют и получают

(2.12)

u_C = 1 / C · ∫ i dt.

Это соотношение является аналогом закона Ома для емкости.

Конструктивно емкость выполняется в виде двух проводников разделенных слоем диэлектрика. Форма проводников может быть плоской, трубчатой, шарообразной и др.

Единицей измерения емкости является фарада:

1Ф = 1Кл / 1В = 1Кулон / 1Вольт.

Оказалось, что фарада является большой единицей, например, емкость земного шара равна ≈ 0,7 Ф. Поэтому чаще всего используют дробные значения

1 пФ = 10^–12 Ф, (пФ – пикофарада);
1 нФ = 10^–9 Ф, (нФ – нанофарада);
1 мкФ = 10^–6 Ф, (мкФ – микрофарада).

Условным обозначением емкости является символ

Основные свойства простейших цепей переменного тока

Простейшие цепи – цепи, содержащие один элемент.

Участок цепи, содержащий активное сопротивление (рис. 2.6).

Рис. 2.6

Зададимся изменением тока в резисторе по синусоидальному закону

i(t) = I_mR sin(ωt + ψ_i).

Воспользуемся законом Ома для мгновенных значений тока и напряжения

u(t) = R i(t)

и получим

(2.13)

u(t) = R I_mR sin(ωt + ψ_i).

Формальная запись синусоидального напряжения имеет вид

(2.14)

u(t) = U_mR sin(ωt + ψ_u)

Соотношения (2.13) и (2.14) будут равны если будут выполнены условия равенства амплитуд и фаз

(2.15)

U_mR = R I_mR,

(2.16)

ψ_u = ψ_i.

Соотношение (2.15) может быть записано для действующих значений

(2.17)

U_R = R I_R.

Соотношение (2.16) показывает, что фазы напряжения и тока в резисторе совпадают. Графически это представлено на временной диаграмме (рис. 2.7) и на комплексной плоскости (рис. 2.8).

Рис. 2.7 и 2.8

Участок цепи, содержащий идеальную индуктивность (рис 2.9)

Рис. 2.9

Зададим изменение тока в индуктивности по синусоидальному закону

i(t) = I_mL sin(ωt + ψ_i).

Используем уравнение связи между током и напряжением в индуктивности

u_L = L · di / dt

и получим

u_L(t) = ωL · I_mL cos(ωt + ψ_i).

Заменим cos на sin и получим

(2.18)

u_L(t) = ωL · I_mL sin(ωt + ψ_i + 90°).

Формальная запись синусоидального напряжения имеет вид

(2.19)

u_L(t) = U_mL sin(ωt + ψ_u).

Соотношения (2.18) и (2.19) будут равны если выполняется условие равенства амплитуд и фаз

(2.20)

U_mL = ωL · I_mL,

(2.21)

ψ_u = ψ_i + 90°.

Уравнение (2.20) можно переписать для действующих значений

(2.22)

U_L = ωL · I_L.

Уравнение (2.21) показывает, что фаза тока в индуктивности отстает от фазы напряжения на 90°. Величину X_L = ωL в уравнении (2.20) называют индуктивным сопротивлением. Единицей его измерения является Ом. Графически электрические процессы в индуктивности представлены на рис. 2.10, 2.11.

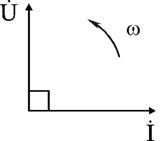
Рис. 2.10 и 2.11

3. Участок цепи, содержащий ёмкость (рис. 2.12)

Рис. 2.12

Зададим изменение тока в емкости по синусоидальному закону

i(t) = I_mC sin(ωt + ψ_i).

Используем уравнением связи между током и напряжением в емкости

u_C = 1 / C · ∫ i dt,

и получим

u_C = 1 / (ωC) · I_mC (-cos(ωt + ψ_i)).

Заменим –cos на sin

(2.23)

u_C = 1 / (ωC) · I_mC sin(ωt + ψ_i - 90°).

Формальная запись синусоидального напряжения имеет вид

(2.24)

u_C = U_mC sin(ωt + ψ_u).

Соотношения (2.23) и (2.24) будут равны если выполняется условие равенства амплитуд и фаз

(2.25)

U_mC = 1 / (ωC) · I_mC,

(2.26)

ψ_u = ψ_i - 90°.

Уравнение (2.25) можно переписать для действующих значений

(2.27)

U_C = 1 / (ωC) · I_C.

Уравнение (2.26) показывает, что фаза напряжения в емкости отстает от фазы тока на 90°. Величину X_C = 1 / (ωC) в уравнении (2.25) называют емкостным сопротивлением цепи и измеряют его в Омах. Графически электрические процессы в емкости представлены на рис. 2.13, 2.14.

Рис. 2.13 и 2.14