
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямой метод стандартизации. Если в распоряжении исследователя имеются возрастные коэффициенты смертности, но неизвестны данные о возрастной структуре сравниваемых населений
Если в распоряжении исследователя имеются возрастные коэффициенты смертности, но неизвестны данные о возрастной структуре сравниваемых населений, то индексный метод применить невозможно. В таком случае можно использовать прямой метод стандартизации. В принципе этот метод очень схож с индексным методом. Разница лишь в том, что неизвестные данные о фактической возрастной структуре населений (как правило, отличной друг от друга) заменяются произвольно выбранной структурой другого населения (одного для всех сравниваемых населений). Таким путем влияние различий возрастной структуры на величины общих коэффициентов устраняется (элиминируется), они искусственно (условно) приводятся к одинаковой возрастной структуре, которая принимается за стандарт (слово «стандарт» в данном случае, так же как и «стандартизация», вряд ли можно признать удачным наименованием, но это уже очень старая всемирная традиция, и к ней привыкли все специалисты).
Вернемся снова к формуле общего коэффициента смертности в ее структурном выражении: т = тxwx,где все условные обозначения те же, что и в предыдущем разделе (об индексном методе). Предположим, что мы хотим сравнить два или более общих коэффициента смертности и при этом установить, в какой степени различия между этими коэффициентами (в динамике или в статике) обусловлены различиями в уровнях смертности и в какой — различиями возрастных структур сравниваемых населений (или населения, если выясняется изменение уровня смертности одного и того же населения в динамике). При этом напомню, что по условию ни одна из возрастных структур нам не известна. Формула, приведенная в начале этого абзаца, примет следующий вид: mСТ = mxwx0, где тСТ — стандартизованный общий коэффициент смертности; тх, — фактические возрастные коэффициенты смертности; wх0 — возрастная структура населения, принятого за стандарт (или, как говорят, «стандарт-населения»).
Рассмотрим теперь применение прямого метода стандартизации коэффициентов смертности на том же примере, который использовался для демонстрации индексного метода в предыдущем параметре. Делаю это для того, чтобы можно было сравнить результаты применения разных методов для одной и той же цели (таблица 6.3).
Таблица 6.3
Стандартизация динамики общих коэффициентов смертности населения России за 1990—1995 гг. прямым методом
| Возрастные группы (лет) | Возрастные коэффициенты смертности mx, ‰ | Возрастная структура населения Украины по переписи 1989 г., принятая за стандарт wx0, в долях единицы | mxwx0 | ||
| 0—4 | 3,9 | 4,1 | 0,0737 | 0,2874 | 0,3022 |
| 5—9 | 0,5 | 0,6 | 0,0718 | 0,0359 | 0,0431 |
| 10—14 | 0,4 | 0,5 | 0,0703 | 0,0281 | 0,0352 |
| 15—19 | 1,1 | 1,6 | 0,0690 | 0,0759 | 0,1104 |
| 20—24 | 1,7 | 2,7 | 0,0652 | 0,1108 | 0,1760 |
| 25—29 | 2,1 | 3,4 | 0,0769 | 0,1615 | 0,2615 |
| 30—34 | 2,7 | 4,6 | 0,0758 | 0,1819 | 0,3487 |
| 35—39 | 3,6 | 6,3 | 0,0727 | 0,2617 | 0,4580 |
| 40—44 | 5,0 | 8,9 | 0,0526 | 0,2630 | 0,4681 |
| 45 — 49 | 7,6 | 12,3 | 0,0626 | 0,4758 | 0,7700 |
| 50—54 | 10,3 | 17,1 | 0,0720 | 0,7416 | 1,2312 |
| 55—59 | 15,2 | 21,4 | 0,0574 | 0,8725 | 1,2284 |
| 60—64 | 22,0 | 29,7 | 0,0628 | 1,3816 | 1,8652 |
| 65—69 | 29,6 | 39,2 | 0,0393 | 1,1633 | 1,5406 |
| 70—74 | 45,7 | 51,3 | 0,0275 | 1,2568 | 1,4108 |
| 75—79 | 71,6 | 78,2 | 0,0277 | 1,9833 | 2,1661 |
| 80—84 | 114,4 | 123,2 | 0,0150 | 1,7160 | 1,8480 |
| 85 и старше | 201,8 | 214,4 | 0,0077 | 1,5539 | 1,6509 |
| Итого | 11,2 | 15,0 | 1,0000 | 12,5510 | 15,9144 |
Теперь вычислим индексы динамики общих коэффициентов смертности в России за 1990 — 1995 гг. Индекс динамики фактических общих коэффициентов уже известен из предыдущего раздела. Он равен:
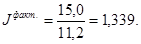
Индекс динамики стандартизованных коэффициентов смертности будет иным:
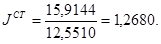
Хотя по условию задачи нам не известна возрастная структура на начало и конец изучаемого периода, мы можем узнать ее влияние на динамику общего коэффициента смертности. Для этого вспомним взаимосвязь трех индексов динамики общего коэффициента смертности из предыдущего раздела: Jm = Jmx x Jwx, т.е. индекс динамики фактических общих коэффициентов смертности равен произведению двух индексов, первый из которых характеризует изменение величины общего коэффициента смертности за счет действительного изменения смертности, а второй индекс — изменение той же величины общего коэффициента смертности за счет изменения возрастной структуры населения. Таким образом, по двум известным элементам вышеприведенного уравнения взаимосвязи трех индексов нетрудно определить третий индекс:
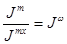 . Отсюда: 1,339/1,268 = 1,056.
. Отсюда: 1,339/1,268 = 1,056.
Окончательный вывод: уровень смертности населения в России увеличился за 1990—1995 гг. на 26,8% (а не на 33,9%, как свидетельствует изменение общего коэффициента смертности), а еще 5,6% роста — результат изменения (постарения) возрастной структуры населения. Полученные прямым методом стандартизации коэффициентов результаты несколько отличаются от аналогичных результатов, полученных с помощью индексного метода. Это результат грубости расчетов, их приблизительности. Но все же различия невелики.
Дата добавления: 2015-04-16; просмотров: 222; Мы поможем в написании вашей работы!; Нарушение авторских прав |