Примеры решения задач. Задача на соединения конденсаторов.

Задача на соединения конденсаторов.

В задании представлены схемы смешанного соединения конденсаторов. Они складываются из последовательного и параллельного соединения.

Формула расчета конденсаторов для последовательного соединения:

С общ.=( С1* С2) / ( С1+ С2)

Формула расчета конденсаторов для параллельного соединения:

С общ.= С1+ С2+…..

Прежде чем сразу начать рассчитывать конденсаторы, нужно сначало упростить схему, поочередно объединив конденсаторы.

Смешанное соединение.

В схеме дано U=100В и емкости всех конденсаторов: С₁=6мкФ, С₂=1,5мкФ, С₃=3мкФ, С₄=3мкФ, С₅=6мкФ. Определить эквивалентную емкость всей цепи, заряд, напряжение на каждом конденсаторе.

Решение:

Конденсаторы С₂ и С₃ соединены последовательно. Их заменим одним конденсатором с эквивалентной емкостью:

С₂₃= С₂ · С₃ / (С₂ + С₃)=1,5·3/(1,5+3)=1мкФ.

Аналогично этому С₄ и С₅ заменим эквивалентным конденсатором емкостью:

С₄₅= С₄ · С₅ / (С₄ + С₅)=3·6/(3+6)=2мкФ.

После замены схема упростится.

Емкости С₂₃ и С₄₅ соединены параллельно. Их эквивалентная емкость С_2-5= С₂₃+С₄₅ =1+2=3мкФ.

После этого схему можно заменить на другую.

Емкости С₁ и С_2-5 соединены последовательно.

Поэтому их эквивалентная емкость:

С= С₁ и С_2-5 /( С₁+С_2-5) =6·3/(6+3)=2мкФ.

Таким образом, постепенно преобразуя изначальную схему приводим ее к простейшему виду с одной емкостью.

Задача на законы Кирхгофа

В задачах нужно знать первый и второй закон Кирхгофа:

ΣI=0; ΣЕ=ΣI*R

Т.е. I1+I2+I3+…=0 – первый закон Кирхгофа

Задача разбирается по частям, относительно узлов схемы.

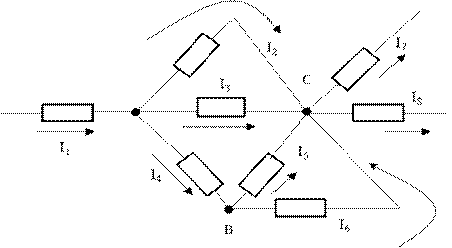
Дано:

I₇=15A

I₅=10A

I₈=5A

I₆=7A

I₃=2А

I₂=?

I₄=?

I₁=?

Решение:

I₇+ I₈ = I₆+ I₅+I₃+ I₂

15+5=7+10+2+ I₂

20=19+ I₂

1А= I₂

I₅+ I₆ = I₄

10+7= I₄

17= I₄

I₁ =I₂+ I₃+I₄

I₁=20А

Задача на сложные электрические цепи

Задачи на сложные цепи решаются разными способами и методами. В задании предлагаются задачи, в основном, на узловое напряжение и метод контурных токов.

В этой задачи нужно составить уравнения по методу контурных токов. Для этого в сехеме нужно выделить контуры и обозначить контурные токи, уравнения составлять относительно 2 закона Кирхгофа.Учитывать направления обхода контура, которое выбирается произвольно.

Решение:

E₁+E₂=I_I(R₃+R₄+R₁₀+R₁₁)-I_III(R₁₀+R₁₁)

E₂+E₃=I_II(R₂+R₉+R₁₀+R₁₁+R₁₂)-I_III(R₉)-I_IV(R₁₂)

E₄+E₃=I_III(R₁+R₉+R₇+R₈+R₁₃)-I_II(R₉)-I_IV(R₁₃)

E₅=I_IV(R₅+R₆+R₁₂+R₁₃)-I_III(R₁₃)-I_II(R₁₂)