Закон Ома для магнитной цепи

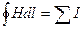
- линейный интеграл от вектора напряженности по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром – полному току (I_полн). Для практических целей наибольший интерес представляет частный случай, когда контур интегрирования проходит внутри обмотки с числом витков w и током IВ этом случае полный ток 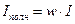, запишем

Сумму токов - wI через поверхность, ограниченную контуром интегрирования, называют магнитодвижущей силой F,

F = wI.

Если учесть, что угол между векторами Ни dl равен нулю и значение Н в любой точке контура интегрирования одинаково, среднее значение напряженности магнитного поля определится как

.

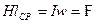Из полученного соотношения следует, что напряженность магнитного поля Н не зависит от магнитных свойств магнитопровода, а прямо пропорциональна току в обмотке. Точнее равна МДС обмотки, приходящейся на единицу длины средней силовой линии магнитопровода.

Исходя из соотношений Ф =ВS и В = μ_a Н получим

Ф = μ_a НS = μ_a S(I w / l) = I w / ( l / μ_a S) = F/R_м.

Это выражение называют законом Ома для магнитной цепи. При этом величину R_м = l / μ_a S принято называть магнитным сопротивлением магнитопровода (по аналогии с электрическим сопротивлением).

При анализе магнитных цепей вводят понятие разности магнитных потенциалов между двумя точками магнитной цепи, которая приравнивается к магнитному напряжению U_{м ab}

U_{м ab} = Н l _ab .