
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет параметров цепи методом законов Кирхгофа
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

ЗАДАНИЕ
Для электрической цепи, соответствующей номеру варианта и графа необходимо выполнить следующие задания (указаны в содержании):

Параметры электрической схемы
| Номер варианта задания | Номер рисунка (графа) | Параметры электрической схемы | ||||||||
| R0 | R1 | R2 | R3 | R4 | R5 | E1 | E3 | J2 | ||
| Ом | B | A | ||||||||
| 0,5 |
Содержание
| Наименование пункта | Стр. | |
| 1. | Анализ электрической цепи: обозначение ветвей, узлов, дерево графа и выбор независимых контуров | |
| 2. | Расчет параметров цепи методом законов Кирхгофа | |
| 3. | Расчет параметров цепи методом контурных токов | |
| 4. | Расчет параметров цепи методом узловых потенциалов | |
| Сводная таблица результатов расчетов значений токов ветвей | ||
| 5. | Расчет тока ветви методом эквивалентного источника | |
| 6. | Анализ баланса мощностей для схемы по результатам расчетов, выполненных одним их методов (определение суммарной мощности источников и суммарной мощности потребителей) | |
 7. 7.
| Построение потенциальной диаграммы |
1. Анализ электрической цепи: обозначение ветвей, узлов, дерево графа и выбор независимых контуров
Преобразуем идеализированный источник тока в идеализированный источник электродвижущей силы (ЭДС):
 |
Þ
Отсюда, E2 = JR2 = 0,5 ∙ 12 = 6 (В)
Выполним эквивалентное преобразование§ параллельного соединения сопротивлений R4 и R5

Þ 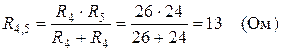
 Отсюда, схема электрической цепи выглядит так :
Отсюда, схема электрической цепи выглядит так :
Рассматриваемая схема содержит :
· число узлов (У): 3 узла (a, b, c);
· число ветвей (В) 5 ветвей (a, R0 , c; a, R3,E3 , b; a, R4 5 , b; b, R1 , E1 , c;
a, R2 , E2 , c);
· число независимых контуров: Nk= В – (У – l ) = 5 – ( 3 – l ) = 3.
Определим независимых контуров§. Для этого вынесем узлы схемы и соединим их ветвями так, что бы не образовывалось контуров. Построим дерево графа:
 |
Выберем в качестве ветвей дерева ветви 1 и 4, 5.
Ветви 0, 3 и 2 являются контурообразующими.
Количество независимых контуров – 3.
Расчет параметров цепи методом законов Кирхгофа
 |
Составим систему уравнений согласно законам Кирхгофа:
согласно первому закону Кирхгофа для узлов§:
a: I2 – I4 5 – I3 + I0 = 0 ;
b: I4.5 + I3 – I1 = 0
согласно второму закону Кирхгофа для контуро⧧:
I: I3 R3 – I45 R4.5 = E3
II: – I0 R0 – I1 R1 – I3 R3 = – E1 – E3
III: I45 R4.5 + I1 R1 + I2 R2 = E1 + E2
Для определения значений токов воспользуемся матричным методом решения системы линейных независимых уравнений:  . Запишем матрицу коэффициентов при неизвестных токах:
. Запишем матрицу коэффициентов при неизвестных токах:
| I0 | I1 | I2 | I3 | I4 | B | |
| а | –1 | –1 | ||||
| b | –1 | |||||
| I | R3 | –R4.5 | E3 | |||
| II | –R0 | –R1 | –R3 | –E1 – E3 | ||
| III | R1 | R2 | R4.5 | E1 + E2 |
Решая систему уравнений относительно искомого тока, находим:
I0 = ∆0/∆ = 1,21 (А);
I1 = ∆1/∆ = 2,51 (А);
I2 = ∆2 /∆= 1,31 (А);
I3 = ∆3/∆ = 1,71 (А);
I45 = ∆45/∆ = 0,81 (А).
Для оценки правильности решения воспользуемся методом баланса мощностей (удобнее сразу проверить правильность полученного решения):
∑Рист = E3 I3 + E1 I1 + E2 I2 = 199,619 (Вт)
∑Рпотр = I02 R0 + I12 R1 + I22 R2 + I32 R3 + I42 R4.5 = 199,619 (Вт)
Сравним суммы мощностей источников и потребления.
Абсолютная погрешность составляет:
∑Рпотр – ∑Рист = 0 (Вт)
Дата добавления: 2015-04-16; просмотров: 225; Мы поможем в написании вашей работы!; Нарушение авторских прав |