Основные операции и элементы алгебры логики.

Основой построения любого устройства, использующего цифровую информацию, являются элементы двух типов: логические и запоминающие. Логические элементы выполняют простейшие логические операции над цифровыми сигналами. Запоминающие элементы служат для хранения цифровой информации (состояния разрядов кодовой комбинации).

Логическая операция состоит в преобразовании по определенным правилам входных цифровых сигналов в выходные. Математически цифровые сигналы обозначают поразрядно символами, например x₁, x₂, x₃, x₄. Их называют переменными. Каждая переменная может принимать значение "0" или "1". Результат логической операции часто обозначают F или Q. Он также может иметь значение "0" или "1". Математическим аппаратом логики является алгебра Буля. В булевой алгебре над переменными "0" или "1" могут выполняться три основных действия: логическое сложение, логическое умножение и логическое отрицание.

Логическое сложение (дизъюнкция или операция ИЛИ) записывается в виде

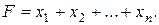
Правила выполнения операции ИЛИ заключаются в следующем:

Логические схемы, реализующие операцию ИЛИ; называют ячейками ИЛИ. Их схемное обозначение приведено на рис. 17.1а. Простейшая реализация логической ячейки ИЛИ на диодах приведена на рис. 17.1б. Напряжение на выходе схемы будет равно E (F=1), если хотя бы на один из входов будет подан единичный сигнал.

Логическое умножение (конъюнкция или операция И) записывается в виде

Правила выполнения операции И заключаются в следующем

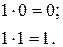(17.2)

Логическое отрицание (инверсия или операция НЕ) записывается в виде

и читается: F равно не x. Правила выполнения операции НЕ заключаются в следующем

(17.3)

Логические схемы, реализующие правило (17.3) называются ячейками НЕ. Их графическое обозначение приведено на рис. 17.3. Операция НЕ может быть реализована схемой транзисторного ключа.

Рассмотренные логические правила и схемы позволяют реализовать сколь угодно сложную логическую функцию. Например, функция

реализуется пятью логическими элементами, в том числе два элемента И, два элемента НЕ и один элемент ИЛИ (см. рис. 17.4).

Все логические элементы выпускаются в микросхемном исполнении. Они входят в состав всех серий цифровых микросхем и имеют следующие условные обозначения:

- элементы "ИЛИ" – ЛЛ;

- элементы "И" – ЛИ;

- элементы "НЕ" – ЛН.

Например, микросхема К555 ЛИ1 имеет в своем составе 4 элемента "И" на два входа каждый.

3.

Теоремы для одной переменной охватывают все операции над переменной x и константами "0" и "1":

1. 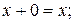2. 3. 4.

5. 6. 7. 8.

9.

Теоремы для двух или более переменных – x и y:

10. Переместительный закон:

11. Сочетательный закон:

12. Распределительный закон:

Доказательство:

Здесь к скобке применена теорема 2.

13. Закон поглощения:

Доказательство:

14.

Доказательство:

15. Закон склеивания:

Доказательство:

16. Закон отрицания (теорема де-Морана)