
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
КОНДЕНСАТОРА
Лабораторная работа №1
ИССЛЕДОВАНИЕ ОДНОФАЗНОЙ ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ
СОЕДИНЕНИЕМ РЕЗИСТОРА, КАТУШКИ ИНДУКТИВНОСТИ И
КОНДЕНСАТОРА
1. ЦЕЛЬ РАБОТЫ
Исследование явления резонанса напряжений и условий его возникновения в неразветвленной цепи переменного тока с последовательным соединением Р, L,С.
При этом необходимо:
- снять показания приборов при изменении значения емкости в цепи;
- рассчитать параметры электрической цепи до резонанса и в момент резонанса;
- построить кривые I,ν0, νL, cosφ=f(C)
- составить отчет.
2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Известно, что при подключении к зажимам цепи с последовательным соединением элементов R,L,С (рис. 1.1) синусоидального напряжения в ней потечет синусоидальный ток, мгновенное значение которого равно i =Im∙ sinω∙t. Для простоты начальная фаза тока Ψi=0$
ω=2π∙f,
где f- частота источника питания промышленной частоты. f=50 Гц.
Реактивные сопротивления цепи определятся как
ΧL= ω∙L=2π∙f;Χc=  =
= 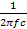 ; Χ= ΧL- ΧC.
; Χ= ΧL- ΧC.
Если ХL > ХС, то в цепи преобладает индуктивная нагрузка, а угол сдвига фаз между током в цепи и напряжением

будет положительным, т.е. напряжение, подведенное к цепи, будет опережать ток в цепи.
Если ХС> ХL , то в цепи преобладает емкостная нагрузка и угол сдвига фаз между током в цепи и приложенным напряжением будет отрицательным, т.е. приложенное напряжение будет отставать по фазе от тока в цепи.
В частности, когда ХL= ХСсдвига фаз между током и напряжением цепи будет равен нулю,т.е. ток в цепи и приложенное напряжение совпадает по фазе.

Равенство этих сопротивлений может быть достигнуто изменением емкости или индуктивности. В данной работе явление резонанса достигается изменением емкости конденсатора до резонансного значения Срез. Резонанс в цепи с последовательным соединением элементов R,L,C называют резонансом напряжения.
Действующее значение тока в цепи определяется законом Ома:
 ;где
;где  =
=  =Ζ
=Ζ
Ζ -полное сопротивление цепи; U - действующее значение напряжения, прикладываемое к цепи.
Напряжения на элементах цепи:
UR=I∙R; UL=I∙ω∙L=I∙XL ; UС=I  =I∙XС
=I∙XС
Когда реактивные сопротивления становятся равными друг другу
ХL = ХCили 2π∙f∙L = 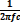 наступает взаимная компенсация ХL и ХC(по фазе они противоположны) и возникает явление резонанса напряжений. В этом случае ток в цепи достигает своего максимального значения, определяемого Imax=
наступает взаимная компенсация ХL и ХC(по фазе они противоположны) и возникает явление резонанса напряжений. В этом случае ток в цепи достигает своего максимального значения, определяемого Imax=  , где R-активное сопротивление цепи.
, где R-активное сопротивление цепи.
Из условия резонанса можно определить резонансную частоту ωp:
ωp∙L=1/ωp∙С
Делаем преобразование  LC=1; отсюда получаем ωp=
LC=1; отсюда получаем ωp=  =
=  , или fp=
, или fp= 
Напряжения на реактивных элементах UL и UС могут оказаться больше напряжения U, приложенного к цепи. Это будет тогда, когда реактивные сопротивления ХL= ХCпревышают активное R, то есть
R<XLp=ωp∙L=L  =
= 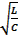 =ρ.
=ρ.
Величина ρ=  называется волновым характеристическим сопротивлением цепи.
называется волновым характеристическим сопротивлением цепи.
Отношение напряжения на реактивных элементах цепи к напряжению на входе называется добротностью контура (цепи):
Qk=  =
= 
Явление резонанса напряжений достаточно опасно для электрической цепи. Если заранее не учитывать явление резонанса напряжений, то это мелет привести к авариям или повреждениям приборов и элементов цепи из-за резких "бросков" тока.
При анализе электрических цепей принято строить векторные диаграммы токов и напряжений ( рис.1.2;1.3,а,б,в ).
Если по горизонтали направить вектор общего для всех элементов цепи тока I, то напряжение на активном сопротивлении R будет совпадать по фазе с током, и его мгновенное значение будет определяться соотношением
UR=i·R
Если ток изменяется по синусоидальному закону I=Im·sinω·t ,то UR=R·Im·sinω·tили для действующего значения в комплексной форме:
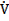 К=R∙
К=R∙ 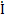
Напряжение на катушке индуктивности
UL=L  =ω·L·Im·sin(ωt+
=ω·L·Im·sin(ωt+  или
или  L=jωLI,
L=jωLI,
а напряжение на конденсаторе
UC=  =
=  Im·sin(ω·t-
Im·sin(ω·t-  или
или  L=-j
L=-j  I.
I.
Для комплексных значений токов и напряжений векторная диаграмма на комплексной плоскости будет иметь вид, показанный на рис.1.2. А для действующих значений напряжений при различных соотношениях реактивных элементов L и С векторные диаграммы представлены на рис 1.3,а,б,в.
3. ПРОГРАММА РАБОТЫ
1. Произвести измерение тока в цепи и напряжений на элементах R,L,C при изменении емкости конденсатора.
2. Отметить значения электрических величин при достижении в цепи явления резонанса, когда ток достигает максимальной величины.
3. Построить векторные диаграммы тока и напряжений до резонанса, когда преобладает индуктивная нагрузка, при наступлении резонанса и после резонанса, когда преобладает емкостная нагрузка.
4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Электрическая схема лабораторной установки приведена на рис.1.4


1. Установить движок ЛАТРа в крайнее левое положение.
2. Подать питание на лабораторный стенд, установив переключатель В1 в положение "Вкл."'. Движком ЛАТРа установить входное напряжение на схему U=80 В.
3. Последовательно, набирая тумблерами на магазине емкостей значение C=0,2,4... Мкф, снять показания приборов и занести их в табл.1.1.
4. Настроить электрическую цепь в резонанс путем изменения емкости цепи. Определить значение резонансной емкости Срез. Измеренные величины при резонансе занести в табл.1.1. Момент резонанса, определить по достижению значения Imax - максимального тока в цепи.
5. Установку привести в исходное положение.
6. Рассчитать величины, указанные в табл. 1.1.
Расчеты производить по формулам;
а) емкостное сопротивление конденсатора
XC=  =
=  ,где f=50Гц; Xcp=
,где f=50Гц; Xcp=  ;
;
б) сопротивление R1=  ;
;
в) индуктивное сопротивление цепи находится из условия резонанса
XL= Xcp=  =
=  ;
;
г) полное сопротивление катушки индуктивности
Ζk=  ;
;
д) активное сопротивление катушки индуктивности
Rk=  ;
;
е) активное сопротивление цепи
R=R1+Rk ;
ж) индуктивность цепи
L=  =
=  ;
;
з) угол сдвига фаз между током и напряжением в цепи
φ=arc tg  ;
;
и) напряжение на индуктивности
UL=I∙XL ;
7. Построить векторные диаграммы для случаев:
1. ХL > ХC
2. ХL = ХC
3. ХL < ХC
8. Построить графики зависимостей:
I,UL,UC, φ=f(c)

5. СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы
2. Электрическая схема лабораторной установки
3. Таблица с результатами измерений и вычислений
4. Расчетные формулы вычислений
5. Векторные диаграммы для трех режимов работы цепи
6. Графики зависимости I,UL,UC,φ=f(C)
7. Краткие выводы
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулировать закон Ома для цепи с последовательным соединением R,L,C,
2. По каким формулам определяются величины цепи?
3. Назовите условие резонанса напряжений в цепи.
4. Как определить резонансную частоту?
5. Почему при резонансе напряжений ток в цепи достигает максимального значения?
6. Чему равны угол сдвига фаз между напряжением и током и коэффициент мощности цепи при резонансе?
Дата добавления: 2015-04-16; просмотров: 343; Мы поможем в написании вашей работы!; Нарушение авторских прав |