Соединение треугольником

Если три фазы нагрузки с фазными сопротивлениям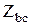и , и включить непосредственно между линейными проводами трехпроводной цепи, то получим соединение приемников треугольником (рисунок 4.9). Из схемы на рисунке 3.9 видно, что если пренебречь сопротивлениями линейных проводов, то фазные напряжения приемника всегда будут равны соответствующим линейным напряжениям источника: 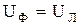. В отличие от соединения звездой фазные и линейные токи не равны между собой. На схеме рисунок 4.9 условно положительные направления фазных токов 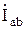, , 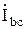соответствуют принятым условно положительным направлениям линейных напряжений 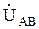, , 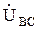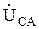. Если сопротивления фаз нагрузки заданы, то фазные токи определяются по формулам:

,

,

.

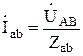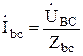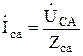Линейные токи определяются по первому закону Кирхгофа для узлов а, b, c:

, , .

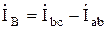Рисунок 4.9 - Трехпроводная трехфазная цепь

при соединении нагрузки треугольником

При симметричной нагрузке = = 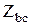фазные токи равны по величине и сдвинуты по фазе относительно соответствующих фазных напряжений на один и тот же угол. Векторная диаграмма напряжений и токов при симметричной нагрузке, соединенной треугольником показана на рисунке 4.10. Из диаграммы следует, что при симметричной нагрузке фазные и линейные токи связаны между собой зависимостью: .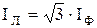

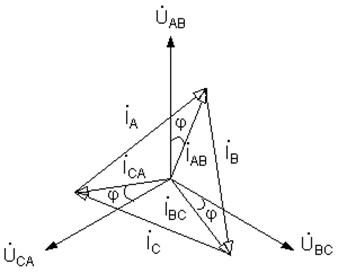
Рисунок 4.10 - Векторная диаграмма для симметричной

нагрузки, соединенной треугольником

При несимметричной нагрузке фазные напряжения на нагрузке, соединенной треугольником остаются неизменными и равными соответствующим линейным напряжениям источника. Фазные токи определяются по тем же формулам, что и при симметричной нагрузке, но вследствие несимметрии нагрузки векторы токов уже не образуют симметричную систему. Для определения линейных токов можно воспользоваться уравнениями, составленными для узлов a, b, c по первому закону Кирхгофа или векторной диаграммой. Топографическая векторная диаграмма фазных напряжений на нагрузке и векторная диаграмма фазных и линейных токов показаны на рисунке 4.11. Из этой векторной диаграммы следует, что независимо от характера нагрузки геометрическая сумма векторов линейных токов в трехпроводной цепи равна нулю: .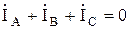

Важной особенностью соединения фаз нагрузки треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным. Будет изменяться только ток данной фазы и линейные токи в линейных проводах, соединенных с этой фазой.