Метод узловых потенциалов

Метод узловых потенциалов основан на уравнениях первого закона Кирхгофа. Потенциал одного из узлов принимается равным нулю. Такое предположение допустимо, так как ток в каждой ветви зависит не от абсолютных значений потенциалов узлов, а от разности потенциалов, приложенной к ветви.

Пусть потенциал узла «d» равен нулю.

Токи в ветвях выражаются на основании закона Ома

,

где – напряжение на зажимах ветви. Знаки перед U_ab и Е выбираются в зависимости от того, совпадает или не совпадает направление тока I с положительными направлениями U_ab и Е.

Таким образом, токи в ветвях равны:

;

;

;

;

;

.

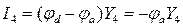Y₁ – Y₆ — проводимости соответствующих ветвей.

Полученные выражения для токов подставляем в исходную систему уравнений, составленную по первому закону Кирхгофа.

;

;

;

После некоторых математических преобразований получаем систему уравнений относительно неизвестных потенциалов , , .

;

;

.

Потенциал основного узла умножается на сумму проводимостей всех ветвей образующих данный узел (для узла «с»— это , , 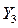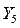). Потенциалы смежных узлов умноженные на проводимость соответствующих смежных ветвей записываются в уравнении со знаком
«-».

В правой части уравнения слагаемые вида записываются со знаком «+», если источник ЭДС направлен к рассматриваемому узлу, в противном случае – со знаком «-».

Найденные потенциалы подставляются в выражения, составленные для сил токов по закону Ома.