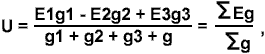КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПОСТОЯННАЯ ОШИБКА ОБУЧАЮЩИХСЯ! ПУТАНИЦА С СООТНОШЕНИЯМИ ЕДИНИЦ ИЗМЕРЕНИЯ В ФОРМУЛАХ, ПРИ УСТАНОВКЕ ДАННЫХ. БУДЬТЕ ВНИМАТЕЛЬНЫ СЕЙЧАС И ВСЕГДА!
Необходимо запомнить (очень важно), что при расчётах цепей, применяются единицы одного уровня.
Например:
если U=nВольт, то I=nАмпер, R=nОм
Выясним:
Что же является причиной, ограничивающей силу тока в проводнике?
Что представляет собой электрический ток в металлах?- Направленное движение электронов.
Если бы электроны в проводнике не испытывали никаких помех в своём движении, то они, будучи приведены в упорядоченное движение, двигались бы по инерции неограниченно долго.
В действительности электроны взаимодействуют с ионами кристаллической решётки металла. При этом замедляется упорядоченное движение электронов и сквозь поперечное сечение проводника за 1 сек их проходит меньше.
Соответственно и переносимый электронами за 1 сек заряд, т.е. уменьшается сила тока. Таким образом, каждый проводник как бы противодействует электрическому току, оказывает ему сопротивление.
Вывод: причина сопротивления – взаимодействие движущихся электронов с ионами кристаллической решётки.
Таким образом, сопротивление проводников зависит от свойств вещества, из которого он изготовлен.
Работа №2.
Включим поочерёдно в цепь проволоки из одинакового материала, но разной длины.
Запишем показания приборов.
Замеряем отрезок: нихром0.4 - 90см = 13.16mA

2) Вывод: сопротивление проводника зависит от его длины; чем длиннее проводник, тем больше сопротивление.
Работа №3.
Включим поочерёдно в цепь проволоки из одинакового материала и одинаковой длины, но с разной площадью поперечного сечения. Запишем показания приборов.
Замеряем отрезок: нихром1.0-30см = 14.21mA

3) Вывод:сопротивление проводника зависит от площади поперечного сечения; чем больше площадь поперечного сечения, тем меньше сопротивление.
Целью проведённых работ является наглядное представление зависимостей
сопротивления проводника:
-от свойств вещества из которого он состоит;
-от поперечного сечения проводника;
-от длины проводника;
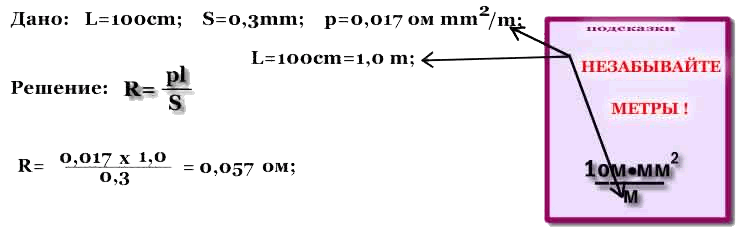
Запишем формулу для расчёта сопротивления проводника:
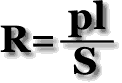
где p - удельное сопротивление вещества.
| Удельное электрическое сопротивление некоторых материалов | |||
| Материал | р, Ом х м2/м | Материал | р, Ом х м2/м |
| Медь | 0,017 | Платино-иридиевый сплав | 0,25 |
| Золото | 0,024 | Графит | |
| Латунь | 0,071 | Уголь | |
| Олово | 0,12 | Фарфор | |
| Свинец | 0,21 | Эбонит | |
| Металл или сплав | |||
| Серебро | 0,016 | Манганин (сплав) | 0,43 |
| Алюминий | 0,028 | Константан (сплав) | 0,50 |
| Вольфрам | 0,055 | Ртуть | 0,96 |
| Железо | 0,1 | Нихром (сплав) | 1,1 |
| Никелин (сплав) | 0,40 | Фехраль (сплав) | 1,3 |
| Хромель (сплав) | 1,5 |
Из формулы следует:

Единица измерения : 1 Ом . мм2 /м, или 1 Ом . м.
На практике часто площадь поперечного сечения выражают в мм2.
Поэтому удобно пользоваться единицей

Выразим длину проводника и площадь поперечного сечения.
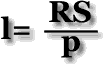
Поскольку R металлов зависит от температуры (R увеличивается при повышении температуры), то в таблице приводятся значения при 20 °С.
Способность проводника пропускать электрический ток называется проводимостью g.
Это величина, обратная сопротивлению, единица измерения которой является сименс:
См = 1/om;
Удельная проводимость: y=1/p;
Лучшие проводники электричества: серебро, медь.
Диэлектрики: фарфор, эбонит.
Силу тока на практике приходится менять (уменьшать или увеличивать). Например, изменяя силу тока в динамике радиоприёмника, мы регулируем громкость; в электродвигателе швейной машины – скорость вращения.
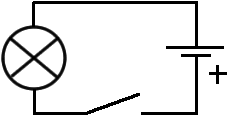
Прибор для регулирования силы тока называется реостатом (он же переменный резистор)
Условное обозначение реостата:

Конструкция реостатов позволяет изменять длину проводника, по которому идёт ток, изменяя при этом сопротивление в цепи.
Путём изменения сопротивления цепи можно влиять на силу тока в ней.
От неё, в свою очередь, зависит действие, оказываемое током на различные устройства в цепи.


В ползунковых реостатах используют проволоку с большим удельным сопротивлением – никелиновую или нихромовую - покрытую тонким слоем окалины, т.е. витки такого реостата изолированы.
Её наматывают на керамический цилиндр. По металлическому стержню перемещается ползунок.
Реостат рассчитан на определённое сопротивление (наибольшую силу тока).
В современных радиоэлектронных устройствах используют резисторы – детали, обеспечивающие заданное (номинальное) электрическое сопротивление цепи.

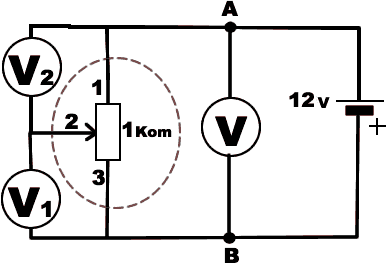
Переменные сопротивления (потенциометры), могут иметь три вывода, один из которых связан с подвижным контактом, скользящим по поверхности проводящего слоя.
Сопротивление между любым крайним выводом переменного резистора и подвижным контактом зависит от положения движка.
Резисторы (постоянное сопротивление).

|
Обязательным условием при изучении электротехники является решение задач.
Это способствует закреплению пройденных материалов.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Диэлектрики. Электрическая емкость.
Материалы, проводящие электрический ток, называются проводниками. В ряде материалов, называемых диэлектриками, электрический ток проводимости не возникает. У таких материалов электрические заряды молекул прочно связаны внутримолекулярными силами и свободных электронов очень мало. К диэлектрикам относятся мрамор, фарфор, слюда, стекло и др. В молекулах диэлектрика очень трудно отделить отрицательный заряд от положительного, но под действием сил электрического поля внутренние молекулярные заряды упруго смещаются: положительные заряды по направлению поля, а отрицательные - в обратном направлении. Таким образом, диэлектрик в электрическом поле поляризуется: на поверхности диэлектрика, обращенной к положительно заряженному проводнику, образуется отрицательный заряд - Q, а на противоположной поверхности - положительный заряд +Q. С устранением внешнего электрического поля эти заряды исчезают.
Система, состоящая из двух проводников, разделенных диэлектриком, называется конденсатором, а проводники - обкладками конденсатора. Если два таких проводника соединить с полюсами источника электрической энергии, то между ними (и разделяющем их диэлектрике) создается электрическое поле. Положим, что конденсатор, состоящий из двух металлических пластинАиБ,являющихся его обкладками, подключен к полюсам источника тока. Если напряжение этого источника U, то очевидно, что обкладки конденсатора находятся под таким же напряжением U. 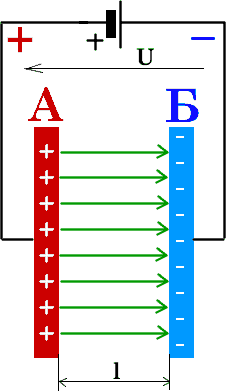 Электрическое поле, возникшее в диэлектрике конденсатора, характеризуется напряженностью. Пусть расстояние между обкладками конденсатора l. Напряженность электрического поля представляет собой отношение напряжения на обкладках к расстоянию между ними, т. е. E=U/l. Если напряжение на обкладках конденсатора выражено в вольтах, а расстояние между параллельно расположенными обкладками - в метрах, то напряженность электрического поля в диэлектрике конденсатора выражается в вольтах на метр (В/м). Чем больше напряжение на обкладках конденсатора, тем больше напряженность поля в его диэлектрике. Обкладки конденсатора, соединенные с полюсами источника энергии, имеют положительный и отрицательный заряды. Величины зарядов, равные между собой по абсолютной величине, пропорциональны напряжению U на обкладках конденсатора. Значит, если величину заряда на одной из обкладок обозначить буквой Q, то можно написать следующее равенство: Q=CU. В этом равенстве величина С является так называемой емкостью конденсатора. Если заряд Q выражен в кулонах, а напряжение U в вольтах, то емкость выражается в Фарадах. Электрическое поле, возникшее в диэлектрике конденсатора, характеризуется напряженностью. Пусть расстояние между обкладками конденсатора l. Напряженность электрического поля представляет собой отношение напряжения на обкладках к расстоянию между ними, т. е. E=U/l. Если напряжение на обкладках конденсатора выражено в вольтах, а расстояние между параллельно расположенными обкладками - в метрах, то напряженность электрического поля в диэлектрике конденсатора выражается в вольтах на метр (В/м). Чем больше напряжение на обкладках конденсатора, тем больше напряженность поля в его диэлектрике. Обкладки конденсатора, соединенные с полюсами источника энергии, имеют положительный и отрицательный заряды. Величины зарядов, равные между собой по абсолютной величине, пропорциональны напряжению U на обкладках конденсатора. Значит, если величину заряда на одной из обкладок обозначить буквой Q, то можно написать следующее равенство: Q=CU. В этом равенстве величина С является так называемой емкостью конденсатора. Если заряд Q выражен в кулонах, а напряжение U в вольтах, то емкость выражается в Фарадах. 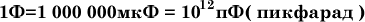 Емкость конденсатора зависит от обкладок, расстояния между ними и диэлектрической проницаемости. Емкость конденсатора тем больше, чем больше площадь S его обкладок и диэлектрическая проницаемость среды, разделяющей их, а также, чем меньше расстояние между обкладками.
Заряд и разряд конденсатора Подключаем конденсатор к источнику энергии, происходит заряд конденсатора до напряжения между обкладками U, равного напряжению источника Е. Обкладка, соединенная с положительным полюсом источника, получит положительный заряд, вторая обкладка — равный по величине отрицательный заряд Q=CU. Для заряда конденсатора необходимо, чтобы одна из обкладок потеряла, а другая приобрела некоторое количество свободных электронов. Электроны движутся от одной обкладки конденсатора на другую под действием напряжения источника. Движение этих зарядов называется током зарядки конденсатора.
С повышением напряжения на конденсаторе ток заряда уменьшается и становится равным нулю. В начальный момент заряда конденсатора напряжение на нем быстро возрастает, так как ток заряда имеет большую величину зарядов и происходит быстрое накопление зарядов на обкладках конденсатора. С повышением емкости конденсатора возрастает количество зарядов, накапливаемых на его обкладках, а с увеличением сопротивления цепи уменьшается зарядный ток, что замедляет накопление зарядов на этих обкладках. Если заряженный конденсатор замкнуть на какое-либо сопротивление R, то под действием напряжения на конденсаторе будет протекать ток разряда конденсатора. Разряд конденсатора сопровождается переносом электронов с одной пластины (где их избыток) на другую (где их недостаток) и продолжается до тех пор, пока потенциалы обкладок не станут одинаковыми, т. е. напряжение на конденсаторе не уменьшится до нуля. По мере понижения напряжения разрядный ток уменьшается, и перенос зарядов с одной обкладки на другую замедляется. Продолжительность процесса разряда конденсатора зависит от сопротивления цепи и емкости конденсатора. Увеличение сопротивления и емкости увеличивает длительность разряда. С повышением сопротивления разрядный ток уменьшается, замедляя перенос зарядов с одной обкладки на другую; с возрастанием емкости конденсатора увеличивается заряд на обкладках. При неизменном напряжении ток через конденсатор не проходит, конденсатор не пропускает постоянный ток, так как между его обкладками помещен диэлектрик. При заряде конденсатор накапливает электрическую энергию, потребляя ее от источника. Накопленная энергия сохраняется некоторое время. Чем больше емкость конденсатора и напряжение между его обкладками, тем больше энергия, накопленная им.
Так выглядят неполярные конденсаторы. Емкость конденсатора зависит от обкладок, расстояния между ними и диэлектрической проницаемости. Емкость конденсатора тем больше, чем больше площадь S его обкладок и диэлектрическая проницаемость среды, разделяющей их, а также, чем меньше расстояние между обкладками.
Заряд и разряд конденсатора Подключаем конденсатор к источнику энергии, происходит заряд конденсатора до напряжения между обкладками U, равного напряжению источника Е. Обкладка, соединенная с положительным полюсом источника, получит положительный заряд, вторая обкладка — равный по величине отрицательный заряд Q=CU. Для заряда конденсатора необходимо, чтобы одна из обкладок потеряла, а другая приобрела некоторое количество свободных электронов. Электроны движутся от одной обкладки конденсатора на другую под действием напряжения источника. Движение этих зарядов называется током зарядки конденсатора.
С повышением напряжения на конденсаторе ток заряда уменьшается и становится равным нулю. В начальный момент заряда конденсатора напряжение на нем быстро возрастает, так как ток заряда имеет большую величину зарядов и происходит быстрое накопление зарядов на обкладках конденсатора. С повышением емкости конденсатора возрастает количество зарядов, накапливаемых на его обкладках, а с увеличением сопротивления цепи уменьшается зарядный ток, что замедляет накопление зарядов на этих обкладках. Если заряженный конденсатор замкнуть на какое-либо сопротивление R, то под действием напряжения на конденсаторе будет протекать ток разряда конденсатора. Разряд конденсатора сопровождается переносом электронов с одной пластины (где их избыток) на другую (где их недостаток) и продолжается до тех пор, пока потенциалы обкладок не станут одинаковыми, т. е. напряжение на конденсаторе не уменьшится до нуля. По мере понижения напряжения разрядный ток уменьшается, и перенос зарядов с одной обкладки на другую замедляется. Продолжительность процесса разряда конденсатора зависит от сопротивления цепи и емкости конденсатора. Увеличение сопротивления и емкости увеличивает длительность разряда. С повышением сопротивления разрядный ток уменьшается, замедляя перенос зарядов с одной обкладки на другую; с возрастанием емкости конденсатора увеличивается заряд на обкладках. При неизменном напряжении ток через конденсатор не проходит, конденсатор не пропускает постоянный ток, так как между его обкладками помещен диэлектрик. При заряде конденсатор накапливает электрическую энергию, потребляя ее от источника. Накопленная энергия сохраняется некоторое время. Чем больше емкость конденсатора и напряжение между его обкладками, тем больше энергия, накопленная им.
Так выглядят неполярные конденсаторы.
Мы уже знаем, что источник электроэнергии обладает разностью потенциалов, заряженные частицы которых, стремятся друг к другу. Существуют материалы, которые способствуют движению частиц, а так - же есть такие, которые ограничивают их движение.
Закон Кулона гласит: сила взаимодействия двух точечных электрических зарядов прямо пропорциональна произведению количеств электричества в этих зарядах, обратно пропорциональна расстоянию между ними и зависит от среды, в которой находятся заряды.
Пример. Работа тока на электролампу:
Это пример с источником большой мощности, обыкновенная батарейка просто потеряет свой заряд. Следовательно, с уменьшением сопротивления внешней цепи напряжение на источнике тоже уменьшается.
1789–1854)
Лишь в 1811 г. ему удалось сдать экзамены в университете и получить степень доктора философии.
|
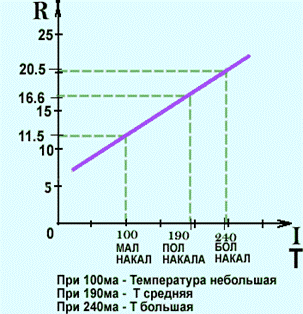
Построим график. Проделанный опыт показывает зависимость сопртотивления от температуры. Опыт основан на приблизительных результатах и расчётах для наглядного показа этой зависимости, без определения температуры нити накала .


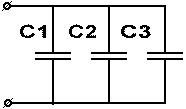
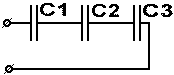 При последовательном соединении конденсаторов уменьшается общая емкость системы, которая будет меньше емкости любого из последовательно включенных конденсаторов, так как последовательное включение подобно увеличению толщины диэлектрика, т. е. расстоянию между обкладками конденсатора. 1/С = 1/С1 + 1/С2 + 1/С3
При последовательном соединении конденсаторов уменьшается общая емкость системы, которая будет меньше емкости любого из последовательно включенных конденсаторов, так как последовательное включение подобно увеличению толщины диэлектрика, т. е. расстоянию между обкладками конденсатора. 1/С = 1/С1 + 1/С2 + 1/С3
 с направлением сил, действующих в нем.
с направлением сил, действующих в нем.


 Георг Симон Ом родился в Эрлангене в семье слесаря. Отец Ома хотел дать детям хорошее образование. Хотя семья постоянно нуждалась в средствах, Георг учился сначала в гимназии, а затем в Эрлангенском университете.
Георг Симон Ом родился в Эрлангене в семье слесаря. Отец Ома хотел дать детям хорошее образование. Хотя семья постоянно нуждалась в средствах, Георг учился сначала в гимназии, а затем в Эрлангенском университете.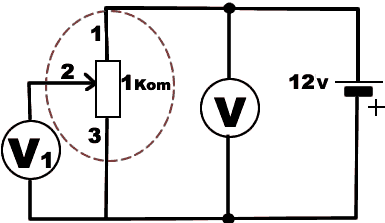






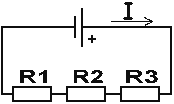 Зная закон Ома представляем: I = E / (R0+R1+R2+R3); где R0 - внутреннее сопротивление источника.
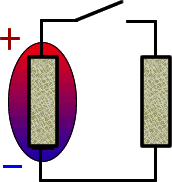
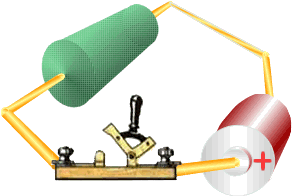
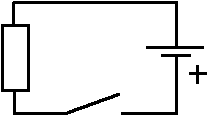
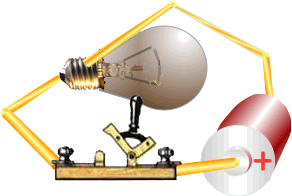
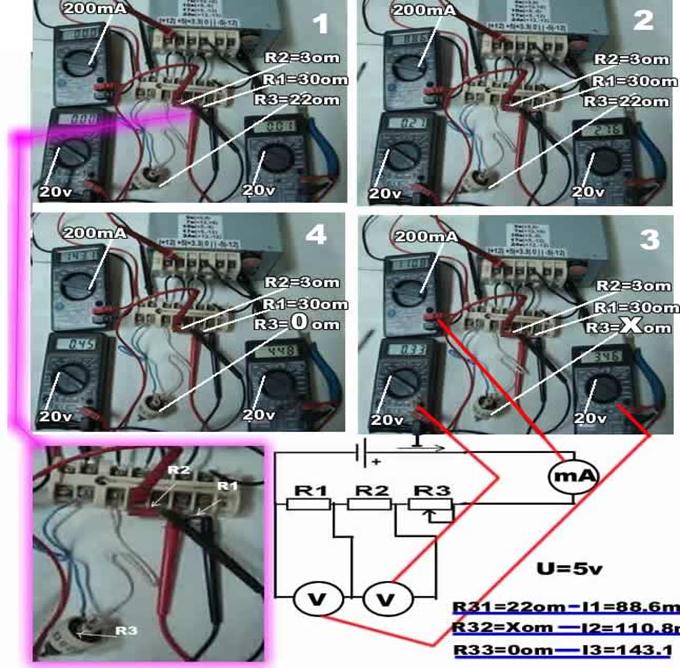
Напряжение на последовательно соединенных нагрузках равно произведению силы тока на сопротивление нагрузки U1 = IR1; U2 = IR2; U3 = IR3. Значит сумма напряжений на нагрузках равна напряжению на источнике. По всей цепи протекает одинаковый ток, значит напряжения пропорциональны их сопротивлениям. U1:U2:U3 = R1:R2:R3. При постоянном напряжении ток зависит от сопротивления цепи. Поэтому изменение сопротивления одной нагрузки ведёт к изменению общего сопротивления всей цепи, тока и напряжения на всех нагрузках. Слегка запутанные представления лабораторных работ, великолепно влияют на усвоение материала и на умение сборки и чтения электрических схем. Рекомендую включать браузер в полноэкранный режим. На первом изображении выключен источник питания и проходит объяснение сборки схемы (в VIDEO-версии). Схема собрана с помощью клеммной колодки , соединения между резисторами посредством перемычек чёрного цвета.
Зная закон Ома представляем: I = E / (R0+R1+R2+R3); где R0 - внутреннее сопротивление источника.
Напряжение на последовательно соединенных нагрузках равно произведению силы тока на сопротивление нагрузки U1 = IR1; U2 = IR2; U3 = IR3. Значит сумма напряжений на нагрузках равна напряжению на источнике. По всей цепи протекает одинаковый ток, значит напряжения пропорциональны их сопротивлениям. U1:U2:U3 = R1:R2:R3. При постоянном напряжении ток зависит от сопротивления цепи. Поэтому изменение сопротивления одной нагрузки ведёт к изменению общего сопротивления всей цепи, тока и напряжения на всех нагрузках. Слегка запутанные представления лабораторных работ, великолепно влияют на усвоение материала и на умение сборки и чтения электрических схем. Рекомендую включать браузер в полноэкранный режим. На первом изображении выключен источник питания и проходит объяснение сборки схемы (в VIDEO-версии). Схема собрана с помощью клеммной колодки , соединения между резисторами посредством перемычек чёрного цвета.

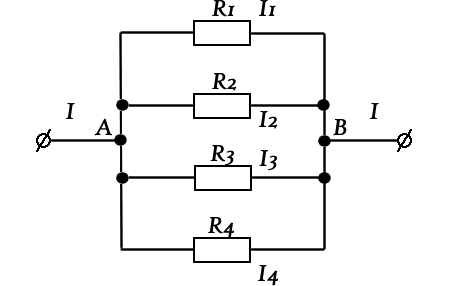
 Полученное выражение имеет большое практическое применение.
Полученное выражение имеет большое практическое применение.


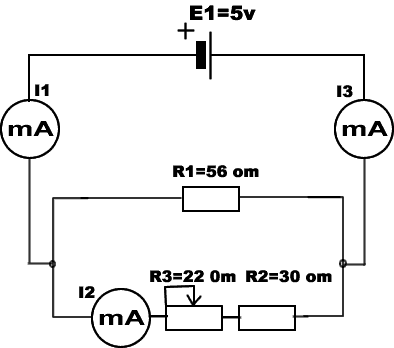
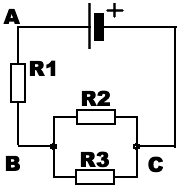 Например, для определения сопротивления между точками A и С сначала находят сопротивление между точками B и C :
Например, для определения сопротивления между точками A и С сначала находят сопротивление между точками B и C :  Потом складывают полученное значение сопротивления с сопротивлением R1:
Потом складывают полученное значение сопротивления с сопротивлением R1: 
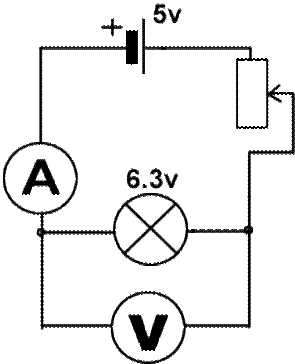
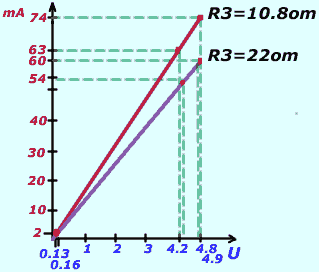
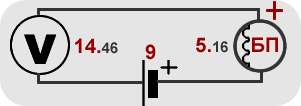
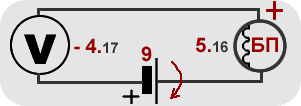
 Подключаем потенциометр к клеммам 5 Вольт источника тока нашего БП. Изменяем напряжение потенциометром. Собираем электрическую цепь по схеме, проводим измерения меняя напряжение и сопротивление цепи.
Подключаем потенциометр к клеммам 5 Вольт источника тока нашего БП. Изменяем напряжение потенциометром. Собираем электрическую цепь по схеме, проводим измерения меняя напряжение и сопротивление цепи.















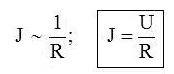




 Двухполюсники, содержащие источники энергии, называются активными (можно представить как источник).
Двухполюсники, содержащие источники энергии, называются активными (можно представить как источник).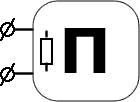
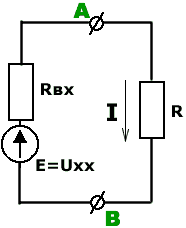 двухполюсник можно заменить эквивалентным генератором(источником напряжения) с ЭДС, равным напряжению холостого хода на зажимах этого двухполюсника и внутренним сопротивлением, равным входному сопротивлению того же двухполюсника, из схемы которого исключены все источники.
двухполюсник можно заменить эквивалентным генератором(источником напряжения) с ЭДС, равным напряжению холостого хода на зажимах этого двухполюсника и внутренним сопротивлением, равным входному сопротивлению того же двухполюсника, из схемы которого исключены все источники.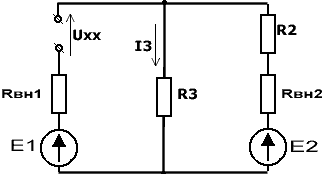
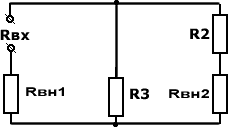
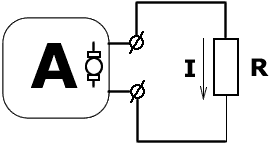
 При проведении опыта холостого хода от активного двухполюсника отключаем сопротивлениеR, в котором необходимо определить ток I.
При проведении опыта холостого хода от активного двухполюсника отключаем сопротивлениеR, в котором необходимо определить ток I.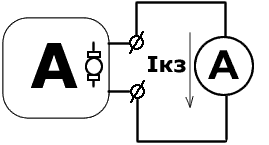
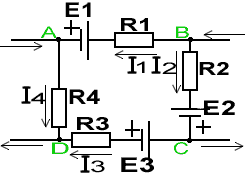
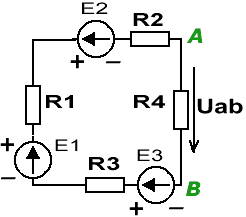
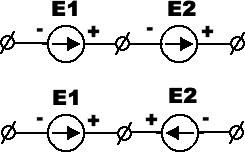
 Если два параллельно соединенных источника энергии, имеющих эдсЕ1 и Е2 и внутренние сопротивления R1, R2, замкнуть какое-либо внешнее сопротивление R, то токи во внешней цепи I и в источниках I1 и I2 можно определить из следующих выражений: I = I1 + I2; I = U/R; I1 = (E1-U) / R1; I2 = (E2-U)/R2; Отсюда ток во внешней цепи: I = (E1 R2 + E2 R1) / (R1 R2 + R R1 + R R2); Токи, протекающие через первый и второй источники энергии: I1= (E1 - I R) / R1 и I2 = (E2 - I R) / R2;
Если два параллельно соединенных источника энергии, имеющих эдсЕ1 и Е2 и внутренние сопротивления R1, R2, замкнуть какое-либо внешнее сопротивление R, то токи во внешней цепи I и в источниках I1 и I2 можно определить из следующих выражений: I = I1 + I2; I = U/R; I1 = (E1-U) / R1; I2 = (E2-U)/R2; Отсюда ток во внешней цепи: I = (E1 R2 + E2 R1) / (R1 R2 + R R1 + R R2); Токи, протекающие через первый и второй источники энергии: I1= (E1 - I R) / R1 и I2 = (E2 - I R) / R2;