Основные теоретические положения. Рассмотрим цепь синусоидального тока с двумя параллельными ветвями

Рассмотрим цепь синусоидального тока с двумя параллельными ветвями. Одна из ветвей состоит из реальной индуктивной катушки с индуктивностью и активным сопротивлением , вторая – из последовательно соединенных резистора 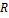и идеального конденсатора . Схема замещения этой цепи приводится на рис.2.1.

Рис. 2.1. Схема цепи с параллельным соединением индуктивной катушки и резистора с конденсатором

Действующее значение модулей токов в ветвях можно определить, используя закон Ома для цепи переменного тока:

; ,

а их комплексы токов (при совмещении вектора напряжения с осью действительных чисел) по формулам:

= ; = ,

где – модуль полного сопротивления индуктивной катушки;

- модуль полного сопротивления ветви с резистором и конденсатором;

– индуктивное сопротивление катушки;

- емкостное сопротивление конденсатора;

– угловая частота переменного тока.

Ток в неразветвленной части цепи определяется по первому закону Кирхгофа

.

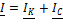Построим векторную диаграмму токов для этой цепи. За исходный примем вектор напряжения, общий для обеих ветвей. Направим вектор напряжения по действительной оси +1 и отложим по отношению к нему векторы токов и . Вектор тока отстает по фазе от вектора напряжения на угол , а вектор тока опережает по фазе вектор напряжения на угол . Вектор тока в неразветвленной части цепи, равный геометрической сумме векторов и , будет опережать или отставать по фазе от вектора напряжения на угол 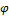(при опережающем токе угол 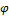считается отрицательным, при отстающем токе – положительным). Знак и величина 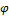для рассматриваемой цепи зависят от состояния длины векторов и , углов и .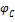

Разложим векторы токов и на активные (совпадающие по фазе с вектором напряжения 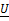) и реактивные (перпендикулярные к вектору напряжения 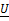) составляющие.

Рис.2.2. Векторная диаграмма цепи с параллельным соединением индуктивной катушки и резистора с конденсатором до резонанса токов

Активные и реактивные составляющие токов ветвей, как видно из рисунка 2.2., можно выразить через модули токов и углы сдвига векторов этих токов относительно вектора напряжения на зажимах цепи

, ,

, .

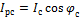Активная и реактивная составляющие тока в неразветвленной части цепи определяется из выражений

,

,

а его модуль

= .

- комплекс тока в неразветвленной части цепи,

= + + .

При вектор тока в неразветвленной части цепи опережает по фазе вектор напряжения на угол 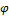(рис. 2.2). Цепь в этом случае является активно-емкостным двухполюсником.

Если цепь является активно-индуктивным двухполюсником. Ток неразветвленного участка такой цепи отстает по фазе от напряжения на входных зажимах.

В цепи с параллельным соединением индуктивной катушки и конденсатора одновременно протекают два энергетических процесса: необратимый процесс поглощения энергии в сопротивлениях и 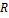, обратимый процесс обмена энергией между переменным магнитным полем индуктивности , электрическим полем емкости и источником питания.

Интенсивность необратимого процесса характеризуется величиной активной мощности , а интенсивность обратимого процесса – величиной реактивной мощности :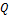

= ;

= .

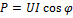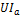Полная мощность цепи определяется выражением

,

а ее модуль

,

где – реактивная мощность индуктивной катушки;

- реактивная мощность конденсатора.

В параллельной цепи с индуктивными и емкостными приемниками возможно явление резонанса токов, при котором ток в неразветвленной части цепи и напряжение на входе совпадают по фазе. Индуктивная и емкостная составляющие токов ветвей при резонансе равны по величине и противоположны по фазе (рис. 2.3). Поэтому они взаимно компенсируются.

Рис.2.3. Векторная диаграмма цепи с параллельным соединением индуктивной катушки и резистора с конденсатором при резонансе токов

Цепь в этом случае будет представлять собой активный двухполюсник. Ток в неразветвленной части цепи имеет только активную составляющую

.

От источника при резонансе токов цепь потребляет одну активную энергию. Она компенсирует потерю энергии в активных сопротивлениях ветвей.

Реактивные индуктивная и емкостная мощности равны по величине , а их колебания находятся в противофазе. Поэтому реактивную мощность цепь от источника не потребляет ( ). В момент резонанса токов происходит только взаимный обмен энергией между электрическим полем конденсатора и магнитным полем катушки.

Резонанс токов в цепи с параллельным соединением индуктивной катушки и резистора с конденсатором можно получить, меняя параметры приемников, такие, как: емкость конденсатора, индуктивность катушки, сопротивление конденсатора, частота питающей сети. Частота питающей сети в этом случае, называется резонансной и определяется из выражения

а для разветвленной цепи с идеальными индуктивными и емкостными элементами

Следует иметь в виду, что в цепи с параллельным соединением индуктивной катушки и резистора с конденсатором при неизменной частоте источника питания изменением одного из параметров резонанс можно получить только при определенных значениях остальных. Например, при изменении резонанс токов можно получить, если При резонанс не случиться ни при каком значении .

При изменении любого из параметров схемы или частоты источника изменяются также полные сопротивления ветвей. Это вызовет изменение величины токов в ветвях, тока в неразветвленной части цепи, углов сдвига фаз токов относительно напряжения на зажимах цепи, активной и реактивной мощностей приемников. Зависимости 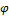, , 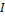, , , , 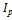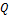от одного из этих параметров (при постоянстве остальных) называемыми резонансными кривыми, используются для анализа режимов работы разветвленных электрических цепей переменного тока.