КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Плоский ламбертовский излучатель
Для плоского ламбертовского излучателя сила света не постоянна 
, следовательно:
(2.4.6)
Таким образом, полный поток от плоского ламбертовского излучателя в телесном угле 
, определяемым плоским углом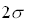 
, можно выразить следующим образом:
| (2.4.7) |
При малых углах выражения (2.4.5) и (2.4.7) для потока излучения сферического и плоского источников дают одинаковый результат.
Решение задач на определение параметров излучателей различных типов рассматривается в практическом занятии "Энергетика световых волн", пункт "1.3. Определение параметров излучателей различных типов".
. Примером может служить белая бумага или молочное стекло. Яркость такой поверхности постоянна по всем направлениям и не зависит от направления падающего света, то есть полностью подчиняется закону Ламберта. Кривая распределения силы света таких поверхностей имеет форму окружности (рис.2.5.1).
Рис.2.5.1. Ламбертовское рассеяние.
Часть падающего потока 
поглощается поверхностью, и рассеивается поток 
: 
(2.5.1)
Коэффициент альбедо 
определяет степень белизны поверхности 
. У абсолютно черного тела 
(ничего не рассеивает, все поглощает), у абсолютно белого тела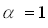 
(все рассеивает, ничего не поглощает)
Альбедо некоторых поверхностей: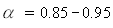 
– очищенный мел, 
– белая бумага для рисования, 
– свежевыпавший снег, 
– песок, 
– черный бархат.
Найдем яркость рассеивателя. Поток 
, следовательно, поток, упавший на рассеиватель: 
(2.5.2)
Рассеянный поток в полусфере: 
(2.5.3) 
, следовательно: 
Отсюда яркость идеального рассеивателя:
– освещенность, создаваемая падающим потоком, 
Рис.2.6.1. Освещенность, создаваемая точечным источником.
Освещенность площадки 
, создаваемая точечным источником: 
Закон обратных квадратов:
Освещенность, создаваемая точечным источником обратно пропорциональна расстоянию от источника до поверхности и прямо пропорционально косинусу угла, между направлением светового потока и нормалью к освещаемой поверхности:
– сила света источника в направлении освещаемой точки.