Методика расчета цепи методом контурных токов

В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.

Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:

1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.

2 Определяем все независимые контуры.

3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.

4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

5 Решаем любым методом полученную систему относительно контурных токов и определяем их.

6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).

7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.

При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.

11.

Число уравнений, подлежащих решению, в ряде случаев можно значительно сократить, используя метод узловых потенциалов, основанный на применении первого закона Кирхгофа и обобщенного закона Ома.

План анализа:

1. Произвольно выбрать направления всех токов в ветвях на исходной схеме.

2. Пронумеровать узлы на исходной схеме. Положить равным нулю потенциал последнего узла. Определить количество уравнений N системы уравнений

N=Nу–Nи–1,

где Nу – число узлов;

Nи – число ветвей, содержащих только идеальные источники ЭДС.

Решить систему уравнений относительно потенциалов узлов V_i

где G_ss – сумма проводимостей ветвей, присоединенных к узлу s, не содержащих источников тока;

G_sq – сумма проводимостей ветвей, непосредственно соединяющих узел s с узлом q;

– алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу s, на их проводимости. Это произведение берется со знаком "плюс", если ЭДС Е направлено к узлу s, иначе "минус";

– алгебраическая сумма источников тока, присоединенных к узлу s. Ток J берется со знаком "плюс", если он направлен к узлу s, иначе "минус".

4. Вычисляют токи из обобщенного закона Ома или первого закона Кирхгофа.

12.

Метод эквивалентного генератора используется при расчёте сложных схем в которых одна ветвь выделяется в качестве сопротивления нагрузки и требуется исследовать и получить зависимость токов в цепи от величины сопротивления нагрузки.

В соответствии с данным методом неизменная часть схемы преобразовывается к одной ветви содержащей ЭДС и внутреннее сопротивление эквивалентного генератора.

Применение метода эквивалентного генератора

ЭДС эквивалентного генератора определяется по формуле:

где: — проводимость участка цепи равная

Для определения эквивалентного сопротивления генератора применяется расчет последовательно и параллельно соединённых сопротивлений, а так же, в случае более сложных схем применяют преобразование треугольник-звезда.

После определения параметров эквивалентного генератора можно определить ток в нагрузке при любом значении сопротивления нагрузки по формуле:

Параметры и можно так же определить по исходной схеме из опытов холостого хода и короткого замыкания .

По опыту холостого хода Для определения в исходной схеме убирают сопротивление нагрузки и полученную схему рассчитывают методом узловых потенциалов. Через полученные значения потенциалов определяют

Значение обычно определяется из опыта короткого замыкания, для этого в исходной схеме сопротивление нагрузки заменяют проводом и по методу контурных токов определяют ток в проводе. После этого эквивалентное сопротивление генератора определяется по формуле:

13.

В электрические цепи могут входить пассивные элементы, электрическое сопротивление которых существенно зависит от тока или напряжения, в результате чего ток не находится в прямо пропорциональной зависимости по отношению к напряжению. Такие элементы и электрические цепи, в которые они входят, называют нелинейными элементами.

14.

Магнитное поле - это особый вид материи, специфической особенностью которой является действие на движущийся электрический заряд, проводники с током, тела, обладающие магнитным моментом, с силой, зависящей от вектора скорости заряда, направления силы тока в проводнике и от направления магнитного момента тела.

15.

Магнитным потоком называют поток вектора магнитной индукции В через некую поверхность. Как определить магнитный поток? Если мы имеем некоторую малую площадку dS, то магнитный поток dФ через нее в пределах которой вектор В неизменен, равен ВndS, где Bn - проекция вектора на нормаль к площадке dS. Сам магнитный поток Ф через конечную поверхность равен интегралу от dФ по этой поверхности. Стоит отметить, что для замкнутой поверхности магнитный поток равен нулю (отсутствует), что отражает отсутствие в природе магнитных зарядов - источников магнитного поля. Единицей магнитного потока в СИ является Вебер (Вб), в СГС — максвелл (Мкс).

Контур, помещенный в однородное магнитное поле, пронизывается магнитным потоком
( потоком векторов магнитной индукции).

Ф - магнитный поток, пронизывающий площадь контура, зависит от
величины вектора магнитной индукции, площади контура и его ориентации относительно линий индукции магнитного поля.

Если вектор магнитной индукции перпендикулярен площади контура, то магнитный поток максимальный.

Если вектор магнитной индукции параллелен площади контура, то магнитный поток равен нулю.

Датский физик X.Эрстед в начале 19 века определил главный в теории электромагнетизма экспериментальный факт, он заключается в следующим, протекание по проводникам электрического тока приводит к появлению в окружающем пространстве магнитного поля.

Этот факт предоставил возможность французскому выдающемуся ученому Лмперу выразить формулировкой закон, который на сегодняшний день имеет название закона полного тока.

Проанализируем рисунок ниже, воображаемый контур L в пространстве, ограничивающий поверхность S.

На этом контуре установим направление обхода так, чтобы движение с конца вектора вдоль контура элементарной площадки dS прослеживалось в направлении против часовой стрелки.

Далее представим то, что поверхность S пронизывается отдельной системой токов, которая может нести как дискретный характер (к примеру, систему отдельных проводников), так и быть непрерывно распределенной (электронный поток может послужить этому примером). Не обуславливая тем временем физической природы данных токов, будем подразумевать для конкретности, что они распределены непрерывно в пространстве с кое-какой плотностью

То теперь полный ток, пронизывающий контур, найдется в виде

Закон полного тока говорит о том, что циркуляция по контуру L вектора напряженности магнитного поля, инициированного протеканием тока равна полному току, то есть.

Закон полного тока формулирует соотношение выше в интегральной форме.

В том, чтобы связать плотность полного тока в данной гонке с напряженностью магнитного поля, то есть найти дифференциальную форму данного закона, надлежит употребить знаменитой теоремой Стикса из векторного анализа, которая говорит нам о том, что для каждого векторного поля А верно равенство

Использовав крайнюю формулу и перестроив с её помощью

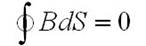
будем располагать

откуда получим из-за произвольности выбранного контура

Формула выше несёт в себе закон полного тока в дифференциальной форме. Заметим, что при помощи закона полного тока в интегральной форме удается разрешить ряд задач, связанных по нахождению магнитного поля заданных токов.