
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розрахунок якості прогнозу.
Мета нашого практичного заняття – отримати практичні навички розрахунку різних мір якості прогнозу, які згадувалися в лекції:
MAD =  (1)
(1)
MSE =  (2)
(2)
MAPE =  (3)
(3)
MPE =  (4)
(4)
де  - загальна кількість спостережень;
- загальна кількість спостережень;
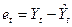 ;
;
 - значення спостереження за досліджуваним процесом (реальні дані) у період t ;
- значення спостереження за досліджуваним процесом (реальні дані) у період t ;
 значення прогнозу (розрахункового значення досліджуваного процесу), отриманого на період t.
значення прогнозу (розрахункового значення досліджуваного процесу), отриманого на період t.
Приклад. Аналізуємо реальний попит на нашу продукцію. Будемо вважати, що кількість запитів на товар є доброю апроксимацією для реального попиту. Маємо статистику про кількість запитів на товар за 10 місяців:
| Період, t | Реальний попит (кількість запитів на товар), Yt |
| Лютий | |
| Березень | |
| Квітень | |
| Травень | |
| Червень | |
| Липень | |
| Серпень | |
| Вересень | |
| Жовтень | |
| Листопад |
Припустимо, що ми використали для отримання прогнозу якийсь з кількісних методів прогнозування. Наприклад, це може бути техніка - підбір певної лінії тренду і прогнозування за знайденим рівнянням тренду. Використаємо її для наочності, але пам¢ятаємо, що прогнозні значення можуть бути отримані будь-яким іншим методом, якість якого для наших даних ми хочемо оцінити.
Отже, для спрощення спробуємо підібрати для наших даних лінійний тренд. Отримаємо:

Отже, рівняння має вигляд

(в якості Х у нас виступає номер періоду t, тобто час).
Прогнозні (розрахункові) значення  можна отримувати не тільки на майбутні періоди, але і для наших спостережень, що вже відбулися. Це є дуже корисним: ми могли б порівняти розрахунки по цьому рівнянню і дані, що мали місце в реальності.
можна отримувати не тільки на майбутні періоди, але і для наших спостережень, що вже відбулися. Це є дуже корисним: ми могли б порівняти розрахунки по цьому рівнянню і дані, що мали місце в реальності.
Отримаємо розрахункові значення 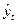 , підставляючи номери періодів у наше рівняння:
, підставляючи номери періодів у наше рівняння:
 53,2185
53,2185
 54,77
54,77
і так далі. Тоді отримуємо прогнозні значення для усієї вибірки спостережень (це можна легко зробити, задавши відповідну формулу в Excel) :
| Період, t. | Реальний попит (кількість запитів на товар), Yt | Прогнозні (розрахункові)  для лінійного тренду для лінійного тренду
|
| 53,2185 | ||
| 54,77 | ||
| 56,3215 | ||
| 57,873 | ||
| 59,4245 | ||
| 60,976 | ||
| 62,5275 | ||
| 64,079 | ||
| 65,6305 | ||
| 67,182 |
Проведемо в Excel необхідні допоміжні розрахунки для оцінки якості прогнозу (їх зведено в таблиці):
| Період, t. | Реальний попит (кількість запитів на товар), Yt | Прогноз | Помилка et | 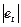
| et2 | ½et ½/Yt | et /Yt | |
| 53,2185 | -0,2185 | 0,2185 | 0,0477422 | 0,00412264 | -0,00412264 | |||
| 54,77 | 3,23 | 3,23 | 10,4329 | 0,05568966 | 0,055689655 | |||
| 56,3215 | -2,3215 | 2,3215 | 5,3893623 | 0,04299074 | -0,04299074 | |||
| 57,873 | 2,127 | 2,127 | 4,524129 | 0,03545 | 0,03545 | |||
| 59,4245 | -4,4245 | 4,4245 | 19,5762 | 0,08044545 | -0,08044545 | |||
| 60,976 | 1,024 | 1,024 | 1,048576 | 0,01651613 | 0,016516129 | |||
| 62,5275 | -0,5275 | 0,5275 | 0,2782563 | 0,00850806 | -0,00850806 | |||
| 64,079 | 0,921 | 0,921 | 0,848241 | 0,01416923 | 0,014169231 | |||
| 65,6305 | -2,6305 | 2,6305 | 6,9195302 | 0,04175397 | -0,04175397 | |||
| 67,182 | 2,818 | 2,818 | 7,941124 | 0,04025714 | 0,040257143 | |||
| Сума: | -0,0025 | 20,2425 | 57,006061 | 0,33990303 | -0,01573871 |
Тепер ми можемо розрахувати наші міри якості цього прогнозу.
MAD = S½et½ / n = 20,2425 / 10 = 2,02425
MSE = S et2 /n = 57 / 10 = 5,7
MAPE = (S (½et½/Yt ) )/n = 0,34 % / 10 = 0,034%
MPE = (S (et /Yt ) )/n = -0,0157 % / 10 = -0,00157 %.
MAD показує, що кожний прогноз відхиляється від реальних даних в середньому на 2,02 випадки попиту.
Значення MSE і MAPE самі по собі не можуть показати, чи є цей прогноз якісним чи ні. Для цього необхідно порівняти їх значення, 5,7 та 0,034 %, з аналогічними величинами, отриманими для якогось альтернативного прогнозу.
Мале значення MPE (-0,00157 %) показує, що модель незміщена: оскільки ця величина є близькою до 0, модель не робить систематичної переоцінки або недооцінки попиту.
Значення мір здаються нам досить малими, отже, прогноз – досить добрим. Але було б добре порівняти результати цієї техніки з якоюсь найбільш простою. Для цих цілей часто використовують наївний прогноз, тобто коли прогноз на завтра є таким, яким є спостереження сьогодні. Тобто, іншими словами, ми не маємо жодної уяви про майбутнє, і можемо очікувати тільки те, що можемо реально спостерігати сьогодні. Якщо наш прогноз виявиться гіршим за ТАКИЙ прогноз, то очевидно, навряд чи доцільно його використовувати. Отже, наведемо аналогічні розрахунки для наївного прогнозу:
.
| Період, t. | Реальний попит (кількість запитів на товар), Yt | Прогноз 
| Помилка et | 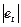
| et2 | ½et ½/Yt | et /Yt |
| - | - | - | - | - | - | ||
| 8,6 | 8,6 | ||||||
| -4 | 7,4 | -7,4 | |||||
| 10,0 | 10,0 | ||||||
| -5 | 9,1 | -9,1 | |||||
| 11,3 | 11,3 | ||||||
| 0,0 | 0,0 | ||||||
| 4,6 | 4,6 | ||||||
| -2 | 3,2 | -3,2 | |||||
| 10,0 | 10,0 | ||||||
| Сума: | 64,2 | 24,8 |
MAD = S½eT½ / n = 39 / 9 = 4,3
MSE = S eT2 /n = 213 / 9 = 23,7
MAPE = (S (½eT ½/YT ) )/n = 64,2% / 9 = 7,1%
MPE = (S (eT /YT ) )/n = 24,8% / 9 = 2,8%.
Отже, видно, що у порівнянні з наївним прогнозом наш перший прогноз видається значно кращим - отже принаймні з цієї точки зору його побудова була доцільною J.
Дата добавления: 2015-04-16; просмотров: 294; Мы поможем в написании вашей работы!; Нарушение авторских прав |