РАБОТА И МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА.

Работа, совершаемая при перемещении положительного заряда Q вдоль некоторого неразветвленного участка электрической цепи, не содержащего источников электрической энергии, от точки a до точки b, равна произведению этого заряда на напряжение U_ab = U между концами участка: А = QU. При равномерном движении за­ряда в течение времени t, т. е. постоянном токе I_аb = I, заряд (ко­личество электричества)

Следовательно, произведенная за время t работа

Основной единицей работы в системе СИ служит джоуль (Дж), 1 Дж= 1 В•А•с.

Для оценки энергетических, условий важно знать, сколь быстро совершается работа. Отношением работы А к соответствующему про­межутку времени t определяют мощность

Основной единицей мощности в системе СИ является ватт (Вт), 1 Вт = 1 Дж/с =1 В•А. Это мощность, при которой за одну се­кунду совершается работа в 1 Дж. Кратные единицы измерения мощ­ности: милливатт (мВт), 1 мВт = 1•10^-3 Вт; киловатт (кВт), 1 кВт = 1•10³ Вт, и мегаватт (МВт), 1 МВт = 1•10⁶ Вт = 1•10³ кВт.

Основная единица работы и энергии джоуль часто слишком мала для оценки энергетических установок. Практической единицей изме­рения электрической энергии служит кило­ватт-час (кВт•ч), т. е. работа, совершаемая при неизменной мощности 1 кВт в течение 1 ч. Так как 1 Вт•с = 1 Дж, то 1 Вт•ч = 3600Вт-с= = 3600 Дж и 1 кВт•ч = 3 600 000 Дж.

Для резистивных. элементов выражение мощности в цепи постоянного тока мож­но преобразовать, заменив в нем на основа­нии закона Ома (1.1) напряжение U = r•I, или I = U/r = gU. Получается три выражения мощности резистивного элемента с сопротивлением r в электрической цепи постоянного тока:

БАЛАНС МОЩНОСТЕЙ

В любой электрической цепи должен соблюдаться энергетический баланс — баланс мощностей: алгебраическая сумма мощнос­тей всех источников энергии (в частности источников тока и ис­точников ЭДС или напряжения) равна арифметической сумме мощнос­тей всех приемников энергии (в частности резистивных элементов):

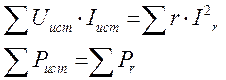
При учете внутренних сопротивлений г_вт источников мощность каждого источника U_истI_ист меньше развиваемой источником мощности Е1_ИСТ на мощность потерь r_втI_вт.

Мощность источника следует считать положительной и записывать в уравнении баланса мощностей со знаком плюс, если положи­тельное направление тока I_ист совпадает с направлением действия ЭДС. В противном случае эту мощность следует считать отрицательной и записывать со знаком минус (например, для заряжаемого аккуму­лятора).

Для любых замкнутых цепей сумма мощностей источников электрической энергии Р_И, равна сумме мощностей, расходуемых в приемниках энергии Р_П. Мощность источников указывает на то, какое количество работы они могут выполнить в электрической цепи каждую секунду. Максимально допустимая мощность приемников это то, что в нормальных условиях может выдержать пассивный элемент. Если превысить допустимую мощность резисторов, обычно указываемую на корпусе, то он может перегреться, его проводящий слой разрушится, почернеет окраска корпуса и деталь выйдет из строя.

Мощность, отдаваемая источниками ЭДС, равна.

где:

U — ЭДС источника (В);

I — ток (А), протекающий через этот источник, причем если положительное направление тока совпадает с направлением ЭДС, в противном случае P = -UI.

Если в резисторе не происходит химических реакций, то мощность выделяется в форме тепла, согласно известному закону Джоуля.

где:

I — постоянный ток (А), протекающий через резистор;

P — мощность потерь, измеряемая в ваттах (Вт);

R — сопротивление резистора (Ом).

Общее количество теплоты, выделяемое током в цепи, не всегда совпадает с соответствующим джоулевым теплом. Так на месте контакта двух различных проводников, помимо джоулева тепла, выделяется также, так называемое тепло Пельтье, зависящее от сторонних ЭДС, определяемых в свою очередь химической природой проводников, их температурой и т.д. При наличии в проводнике градиента температур в нем выделяется еще и теплота Томсона. В большинстве практических случаев при небольших токах теплотой Пельтье и Томсона можно пренебрегать.

Равенство выражений мощностей источников и мощностей приемников называется уравнением баланса мощностей.