
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные топологии ЛВС
Вычислительные машины, входящие в состав ЛВС, могут быть расположены самым случайным образом на территории, где создается вычислительная сеть. Следует заметить, что для способа обращения к передающей среде и методов управления сетью небезразлично, как расположены абонентские ЭВМ. Поэтому имеет смысл говорить о топологии ЛВС.
Топология ЛВС- это усредненная геометрическая схема соединений узлов сети.
Топологии вычислительных сетей могут быть самыми различными, но для локальных вычислительных сетей типичными являются всего три: кольцевая, шинная, звездообразная.
Иногда для упрощения используют термины - кольцо, шина и звезда. Не следует думать, что рассматриваемые типы топологий представляют собой идеальное кольцо, идеальную прямую или звезду.
Любую компьютерную сеть можно рассматривать как совокупность узлов.
Узел - любое устройство, непосредственно подключенное к передающей среде сети.
Топология усредняет схему соединений узлов сети. Так, и эллипс, и замкнутая кривая, и замкнутая ломаная линия относятся к кольцевой топологии, а незамкнутая ломаная линия-к шинной.
Кольцевая топология предусматривает соединение узлов сети замкнутой кривой - кабелем передающей среды (рис. 6.22). Выход одного узла сети соединяется со входом другого. Информация по кольцу передается от узла к узлу. Каждый промежуточный узел между передатчиком и приемником ретранслирует посланное сообщение. Принимающий узел распознает и получает только адресованные ему сообщения.

Рис. 6.22. Сеть кольцевой топологии
Кольцевая топология является идеальной для сетей, занимающих сравнительно небольшое пространство. В ней отсутствует центральный узел, что повышает надежность сети. Ретрансляция информации позволяет использовать в качестве передающей среды любые типы кабелей.
Последовательная дисциплина обслуживания узлов такой сети снижает ее быстродействие, а выход из строя одного из узлов нарушает целостность кольца и требует принятия специальных мер для сохранения тракта передачи информации.
Шинная топология - одна из наиболее простых (рис. 6.23). Она связана с использованием в качестве передающей среды коаксиального кабеля. Данные от передающего узла сети распространяются по шине в обе стороны. Промежуточные узлы не транслируют поступающих сообщений. Информация поступает на все узлы, но принимает сообщение только тот, которому оно адресовано. Дисциплина обслуживания параллельная.
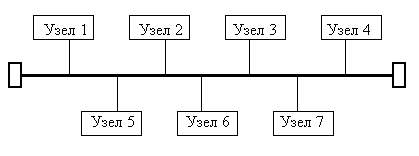
Рис. 6.23. Сеть шинной топологии
Это обеспечивает высокое быстродействие ЛВС с шинной топологией. Сеть легко наращивать и конфигурировать, а также адаптировать к различным системам Сеть шинной топологии устойчива к возможным неисправностям отдельных узлов.
Сети шинной топологии наиболее распространены в настоящее время. Следует отметить, что они имеют малую протяженность и не позволяют использовать различные типы кабеля в пределах одной сети.
Звездообразная топология (рис. 6.24) базируется на концепции центрального узла, к которому подключаются периферийные узлы. Каждый периферийный узел имеет свою отдельную линию связи с центральным узлом. Вся информация передается через центральный узел, который ретранслирует, переключает и маршрутизирует информационные потоки в сети.

Рис. 6.24. Сеть звездообразной топологии
Звездообразная топология значительно упрощает взаимодействие узлов ЛВС друг с другом, позволяет использовать более простые сетевые адаптеры. В то же время работоспособность ЛВС со звездообразной топологией целиком зависит от центрального узла.
В реальных вычислительных сетях могут использоваться более сложные топологии, представляющие в некоторых случаях сочетания рассмотренных.
Выбор той или иной топологии определяется областью применения ЛВС, географическим расположением ее узлов и размерностью сети в целом.
Дата добавления: 2014-11-13; просмотров: 307; Мы поможем в написании вашей работы!; Нарушение авторских прав |