Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 13 страница

Зная поглощательную способность А_l,Т тела при той же длине волны, по яркостной температуре можно определить истинную. Переписав формулу Планка (200.3) в виде

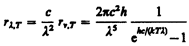
и учитывая это в (201.2), получим

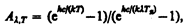
т. е. при известных А_l,Т и l можно определить истинную температуру исследуемого тела.

4. Тепловые источники света. Свечение раскаленных тел используется для создания источников света, первые из которых — лампы накаливания и дуговые лампы — были соответственно изобретены русскими учеными Л. Н. Лодыгиным в 1873 г. и П. Н. Яблочковым в 1876 г.

На первый взгляд кажется, что черные тела должны быть наилучшими тепловыми источниками света, так как их спектральная плотность энергетической светимости для любой длины волны больше спектральной плотности энергетической светимости нечерных тел, взятых при одинаковых температурах. Однако оказывается, что для некоторых тел (например, вольфрама), обладающих селективностью теплового излуче­ния, доля энергии, приходящаяся на излучение в видимой области спектра, значительно больше, чем для черного тела, нагретого до той же температуры. Поэтому вольфрам, обладая еще и высокой температурой плавления, является наилучшим материалом для изготовления нитей ламп.

Температура вольфрамовой нити в вакуумных лампах не должна превышать 2450 К, поскольку при более высоких температурах происходит ее сильное распыление. Максимум излучения при этой температуре соответствует длине волны »1,1 мкм, т. е. очень далек от максимума чувствительности человеческого глаза (»0,55 мкм). Напол­нение баллонов ламп инертными газами (например, смесью криптона и ксенона с добавлением азота) при давлении »50 кПа позволяет увеличить температуру нити до 3000 К, что приводит к улучшению спектрального состава излучения. Однако светоотдача при этом не увеличивается, так как возникают дополнительные потери энергии из-за теплообмена между нитью и газом вследствие теплопроводности и кон­векции. Для уменьшения потерь энергии за счет теплообмена и повышения светоотдачи газонаполненных ламп нить изготовляют в виде спирали, отдельные витки которой обогревают друг друга. При высокой температуре вокруг этой спирали образуется неподвижный слой газа и исключается теплообмен вследствие конвекции. Энергетичес­кий к.п.д. ламп накаливания в настоящее время не превосходит 5%.

§ 202. Виды фотоэлектрического эффекта. Законы внешнего фотоэффекта

Гипотеза Планка, блестяще решившая задачу теплового излучения черного тела, получила подтверждение и дальнейшее развитие при объяснении фотоэффекта — явле­ния, открытие и исследование которого сыграло важную роль в становлении квантовой теории. Различают фотоэффект внешний, внутренний и вентильный. Внешним фотоэлектрическим эффектом (фотоэффектом) называется испускание электронов веществом под действием электромагнитного излучения. Внешний фотоэффект наблюдается в тве­рдых телах (металлах, полупроводниках, диэлектриках), а также в газах на отдельных атомах и молекулах (фотоионизация). Фотоэффект обнаружен (1887 г.) Г. Герцем, наблюдавшим усиление процесса разряда при облучении искрового промежутка уль­трафиолетовым излучением.

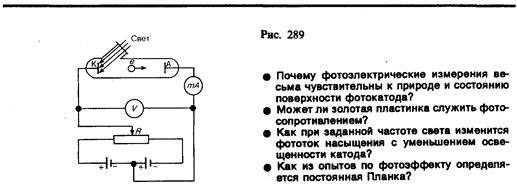
Первые фундаментальные исследования фотоэффекта выполнены русским ученым А. Г. Столетовым. Принципиальная схема для исследования фотоэффекта приведена на рис. 289. Два электрода (катод К из исследуемого металла и анод А — в схеме Столетова применялась металлическая сетка) в вакуумной трубке подключены к бата­рее так, что с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом (через кварцевое окошко), измеряется включенным в цепь миллиамперметром. Облучая катод светом различных длин волн, Столетов установил следующие закономерности, не утратившие своего значения до нашего времени: 1) на­иболее эффективное действие оказывает ультрафиолетовое излучение; 2) под действи­ем света вещество теряет только отрицательные заряды; 3) сила тока, возникающего под действием света, прямо пропорциональна его интенсивности.

Дж. Дж. Томсон в 1898 г. измерил удельный заряд испускаемых под действием света частиц (по отклонению в электрическом и магнитном полях). Эти измерения показали, что под действием света вырываются электроны.

Внутренний фотоэффект — это вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свобод­ные без вылета наружу. В результате концентрация носителей тока внутри тела увеличивается, что приводит к возникновениюфотопроводимости (повышению электропроводности полупроводника или диэлектрика при его освещении) или к возникнове­нию э.д.с.

Вентильный фотоэффект, являющийся разновидностью внутреннего фотоэффек­та, — возникновение э.д.с. (фото-э.д.с.) при освещении контакта двух разных полупро­водников или полупроводника и металла (при отсутствии внешнего электрического поля). Вентильный фотоэффект открывает, таким образом, пути для прямого преоб­разования солнечной энергии в электрическую.

На рис. 289 приведена экспериментальная установка для исследованиявольт-ампер­ной характеристики фотоэффекта — зависимости фототока I, образуемого потоком электронов, испускаемых катодом под действием света, от напряжения U между электродами. Такая зависимость, соответствующая двум различным освещенностям Е, катода (частота света в обоих случаях одинакова), приведена на рис. 290. По мере увеличения U фототок постепенно возрастает, т. е. все большее число фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с различными скоростями. Максимальное значение тока I_нас —фототок насы­щения — определяется таким значением U, при котором все электроны, испускаемые катодом, достигают анода:

где n — число электронов, испускаемых катодом в 1 с.

(202.1)

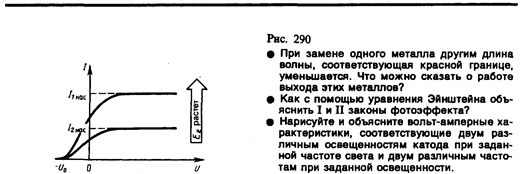
Из вольт-амперной характеристики следует, что при U=0 фототок не исчезает. Следовательно, электроны, выбитые светом из катода, обладают некоторой начальной скоростью v, а значит, и отличной от нуля кинетической энергией и могут достигнуть анода без внешнего поля. Для того чтобы фототок стал равным нулю, необходимо приложитьзадерживающее напряжение U₀. При U=U₀ ни один из электронов, даже обладающий при вылете из катода максимальной скоростью v_max, не может преодолеть задерживающего поля и достигнуть анода. Следовательно,

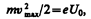
т. е., измерив задерживающее напряжение U₀, можно определить максимальные значе­ния скорости и кинетической энергии фотоэлектронов.

При изучении вольт-амперных характеристик разнообразных материалов (важна чистота поверхности, поэтому измерения проводятся в вакууме и на свежих поверх­ностях) при различных частотах падающего на катод излучения и различных энер­гетических освещенностях катода и обобщения полученных данных были установлены следующиетри закона внешнего фотоэффекта.

I. Закон Столетова: при фиксированной частоте падающего света число фотоэлект­ронов, вырываемых из катода в единицу времени, пропорционально интенсивности света (сила фототока насыщения пропорциональна энергетической освещенности Е_е ка­тода).

II. Максимальная начальная скорость (максимальная начальная кинетическая энер­гия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой n.

III. Для каждого вещества существует красная граница фотоэффекта, т. е. мини­мальная частота n₀ света (зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.

Качественное объяснение фотоэффекта с волновой точки зрения на первый взгляд не должно было бы представлять трудностей. Действительно, под действием поля световой волны в металле возникают вынужденные колебания электронов, амплитуда которых (например, при резонансе) может быть достаточной для того, чтобы электро­ны покинули металл; тогда и наблюдается фотоэффект. Кинетическая энергия вырыва­емого из металла электрона должна была бы зависеть от интенсивности падающего света, так как с увеличением последней электрону передавалась бы большая энергия. Однако этот вывод противоречит II закону фотоэффекта. Так как, по волновой теории, энергия, передаваемая электронам, пропорциональна интенсивности света, то свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла; иными словами, красной границы фотоэффекта не должно быть, что противоречит III закону фотоэффекта. Кроме того, волновая теория не смогла объяснить безынерционность фотоэффекта, установленную опытами. Таким образом, фотоэффект необъясним с точки зрения волновой теории света.

§ 203. Уравнение Эйнштейна для внешнего фотоэффекта. Экспериментальное подтверждение квантовых свойств света

А. Эйнштейн в 1905 г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе предложенной им квантовой теории фотоэффекта. Соглас­но Эйнштейну, свет частотой n не только испускается, как это предполагал Планк (см. § 200), но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых e₀=hn. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализован­ных в пространстве дискретных световых квантов, движущихся со скоростью с рас­пространения света в вакууме. Кванты электромагнитного излучения получили назва­ние фотонов.

По Эйнштейну, каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности света (I закон фотоэффекта). Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно.

Энергия падающего фотона расходуется на совершение электроном работы вы­хода А из металла (см. § 104) и на сообщение вылетевшему фотоэлектрону кинетичес­кой энергии mv²_max/2. По закону сохранения энергии,

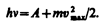(203.1)

Уравнение (203.1) называется уравнением Эйнштейна для внешнего фотоэффекта.

Уравнение Эйнштейна позволяет объяснить II и III законы фотоэффекта. Из (203.1) непосредственно следует, что максимальная кинетическая энергия фотоэлектрона ли­нейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни n от интенсивности света не зависят (II закон фотоэффекта). Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (для данного металла А=const), то при некоторой достаточно малой частоте n=n₀ кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится (III закон фотоэффекта). Согласно изложенному, из (203.1) получим, что

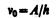(203.2)

и есть красная граница фотоэффекта для данного металла. Она зависит лишь от работы выхода электрона, т. е. от химической природы вещества и состояния его поверхности.

Выражение (203.1) можно записать, используя (202.1) и (203.2), в виде

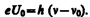
Уравнение Эйнштейна было подтверждено опытами Милликена. В его приборе (1916 г.) поверхность исследуемого металла подвергалась очистке в вакууме. Ис­следовалась зависимость максимальной кинетической энергии фотоэлектронов (изме­нялось задерживающее напряжение U₀ (см. (202.1)) от частоты n и определялась постоянная Планка. В 1926 г. российские физики П. И. Лукирский (1894—1954) и С. С. Прилежаев для исследования фотоэффекта применили метод вакуумного сферического конденсатора. Анодом в их установке служили посеребренные стенки стеклян­ного сферического баллона, а катодом — шарик (R »1,5 см) из исследуемого металла, помещенный в центр сферы. В остальном схема принципиально не отличается от описанной на рис. 289. Такая форма электродов позволила увеличить наклон вольт-амперных характеристик и тем самым более точно определять задерживающее напряжение U₀ (а следовательно, и h). Значение h, полученное из данных опытов, согласуется со значениями, найденными другими методами (по излучению черного тела (§ 200) и по коротковолновой границе сплошного рентгеновского спектра (§ 299)). Все это является доказательством правильности уравнения Эйнштейна, а вместе с тем и его квантовой теории фотоэффекта.

Если интенсивность света очень большая (лазерные пучки; см. § 233), то возможен многофотонный (нелинейный) фотоэффект, при котором электрон, испускаемый метал­лом, может одновременно получить энергию не от одного, а от N фотонов (N=2¸7). Уравнение Эйнштейна для многофотонного фотоэффекта

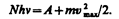
В опытах с фокусируемыми лазерными пучками плотность фотонов очень большая, поэтому электрон может поглотить не одни, а несколько фотонов. При этом электрон может приобрести энергию, необходимую для выхода из вещества, даже под действием света с частотой, меньшей красной границы — порога однофотонного фотоэффекта. В результате красная граница смещается в сторону более длинных волн.

Идея Эйнштейна о распространении света в виде потока отдельных фотонов и квантовом характере взаимодействия электромагнитного излучения с веществом подтверждена в 1922 г. опытами А. Ф. Иоффе и H. И. Добронравова. В электричес­ком поле плоского конденсатора уравновешивалась заряженная пылинка из висмута. Нижняя обкладка конденсатора изготовлялась из тончайшей алюминиевой фольги, которая являлась одновременно анодом миниатюрной рентгеновской трубки. Анод бомбардировался ускоренными до 12 кВ фотоэлектронами, испускаемыми катодом под действием ультрафиолетового излучения. Освещенность катода подбиралась столь слабой, чтобы из него в 1 с вырывалось лишь 1000 фотоэлектронов, а следовательно, и число рентгеновских импульсов было 1000 в 1 с. Опыт показал, что в среднем через каждые 30 мин уравновешенная пылинка выходила из равновесия, т. е. рентгеновское излучение освобождало из нее фотоэлектрон.

Если бы рентгеновское излучение распространялось в виде сферических волн, а не отдельных фотонов, то каждый рентгеновский импульс отдавал бы пылинке очень малую часть своей энергии, которая распределялась бы, в свою очередь, между огромным числом электронов, содержащихся в пылинке. Поэтому при таком механиз­ме трудно вообразить, что один из электронов за такое короткое время, как 30 мин, может накопить энергию, достаточную для преодоления работы выхода из пылинки. Напротив, с точки зрения корпускулярной теории это возможно. Так, если рентгеновс­кое излучение распространяется в виде потока дискретных фотонов, то электрон выбивается из пылинки только тогда, когда в нее попадает фотон. Элементарный расчет для выбранных условий дает, что в среднем в пылинку попадает один фотон из 1,8×10⁶. Так как в 1 с вылетает 1000 фотонов, то в среднем в пылинку будет попадать один фотон в 30 мин, что согласуется с результатами опыта.

Если свет представляет собой поток фотонов, то каждый фотон, попадая в регист­рирующий прибор (глаз, фотоэлемент), должен вызывать то или иное действие незави­симо от других фотонов. Это же означает, что при регистрации слабых световых потоков должны наблюдаться флуктуации их интенсивности. Эти флуктуации слабых потоков видимого света действительно наблюдались С. И. Вавиловым. Наблюдения проводились визуально. Глаз, адаптированный к темноте, обладает довольно резким порогом зрительного ощущения, т. е. воспринимает свет, интенсивность которого не меньше некоторого порога. Для света с l=525 нм порог зрительного ощущения соответствует у разных людей примерно 100—400 фотонам, падающим на сетчатку за 1 с. С. И. Вавилов наблюдал периодически повторяющиеся вспышки света одинако­вой длительности. С уменьшением светового потока некоторые вспышки уже не воспринимались глазом, причем чем слабее был световой поток, тем больше было пропусков вспышек. Это объясняется флуктуациями интенсивности света, т. е. число фотонов оказывалось по случайным причинам меньше порогового значения. Таким образом, опыт Вавилова явился наглядным подтверждением квантовых свойств света.

§ 204. Применение фотоэффекта

На явлении фотоэффекта основано действие фотоэлектронных приборов, получивших разнообразное применение в различных областях науки и техники. В настоящее время практически невозможно указать отрасли производства, где бы не использовались фотоэлементы — приемники излучения, работающие на основе фотоэффекта и преоб­разующие энергию излучения в электрическую.

Простейшим фотоэлементом с внешним фотоэффектом являетсявакуумный фото­элемент. Он представляет собой откачанный стеклянный баллон, внутренняя поверх­ность которого (за исключением окошка для доступа излучения) покрыта фоточувстви­тельным слоем, служащим фотокатодом. В качестве анода обычно используется кольцо или сетка, помещаемая в центре баллона. Фотоэлемент включается в цепь батареи, э.д.с. которой выбирается такой, чтобы обеспечить фототок насыщения. Выбор материала фотокатода определяется рабочей областью спектра: для регистрации видимого света и инфракрасного излучения используется кислородно-цезиевый катод, для регистрации ультрафиолетового излучения и коротковолновой части видимого света — сурьмяно-цезиевый. Вакуумные фотоэлементы безынерционны, и для них наблюдается строгая пропорциональность фототока интенсивности излучения. Эти свойства позволяют использовать вакуумные фотоэлементы в качестве фотометрических приборов, напри­мер фотоэлектрический экспонометр, люксметр (измеритель освещенности) и т. д.

Для увеличения интегральной чувствительности вакуумных фотоэлементов (фототок насыщения, приходящийся на 1 лм светового потока) баллон заполняется раз­реженным инертным газом (Аr или Ne при давлении »1,3¸13 Па). Фототок в таком элементе, называемомгазонаполненным, усиливается вследствие ударной ионизации молекул газа фотоэлектронами. Интегральная чувствительность газонаполненных фо­тоэлементов (» 1 мА/лм) гораздо выше, чем для вакуумных (20—150 мкА/лм), но они обладают по сравнению с последними большей инерционностью (менее строгой про­порциональностью фототока интенсивности излучения), что приводит к ограничению области их применения.

Для усиления фототока применяются уже рассмотренные выше (см. рис. 155) фотоэлектронные умножители, в которых наряду с фотоэффектом используется явление вторичной электронной эмиссии (см. § 105). Размеры фотоэлектронных умножителей немного превышают размеры обычной радиолампы, общий коэффициент усиления составляет »10⁷ (при напряжении питания 1—1,5 кВ), а их интегральная чувствительность может достигать 10 А/лм. Поэтому фотоэлектронные умножители начинают вытеснять фотоэлементы, правда, их применение связано с использованием высоко­вольтных стабилизированных источников питания, что несколько неудобно.

Фотоэлементы с внутренним фотоэффектом, называемыеполупроводниковыми фотоэлементами илифотосопротивлениями (фоторезисторами), обладают гораздо большей интегральной чувствительностью,чем вакуумные. Для их изготовления используются PbS, CdS, PbSe и некоторые другие полупроводники. Если фотокатоды вакуумных фотоэлементов и фотоэлектронных умножителей имеют красную границу фотоэффекта не выше 1,1мкм, то применение фотосопротивлений позволяет производить измере­ния в далекой инфракрасной области спектра (3¸4 мкм), а также в областях рент­геновского и гамма-излучений. Кроме того, они малогабаритны и имеют низкое напряжение питания. Недостаток фотосопротивлений — их заметная инерционность, поэтому они непригодны для регистрации быстропеременных световых потоков.

Фотоэлементы с вентильным фотоэффектом, называемыевентильными фотоэлемен­тами (фотоэлементами с запирающим слоем), обладая, подобно элементам с внешним фотоэффектом, строгой пропорциональностью фототока интенсивности излучения, имеют большую по сравнению с ними интегральную чувствительность (примерно 2—30 мА/лм) и не нуждаются во внешнем источнике э.д.с. К числу вентильных фотоэлементов относятся германиевые, кремниевые, селеновые, купроксные, серни­сто-серебряные и др.

Кремниевые и другие вентильные фотоэлементы применяются для создания со­лнечных батарей, непосредственно преобразующих световую энергию в электрическую. Эти батареи уже в течение многих лет работают на космических спутниках и кораблях. К.п.д. этих батарей составляет »10% и, как показывают теоретические расчеты, может быть доведен до »22%, что открывает широкие перспективы их использования в качестве источников электроэнергии для бытовых и производственных нужд.

Рассмотренные виды фотоэффекта используются также в производстве для конт­роля, управления и автоматизации различных процессов, в военной технике для сигнализации и локации невидимым излучением, в технике звукового кино, в различ­ных системах связи и т. д.

§ 205. Масса и импульс фотона. Давление света

Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и рас­пространяется дискретными порциями (квантами), названнымифотонами. Энергия фотона e₀=hn. Его масса находится из закона взаимосвязи массы и энергии (см. (40.8)):

(205.1)

Фотон — элементарная частица, которая всегда (в любой среде!) движется со скоро­стью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.

Импульс фотона р_g получим, если в общей формуле (40.7) теории относительности

положим массу покоя фотона 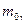= 0:

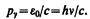(205.2)

Из приведенных рассуждений следует, что фотон, как и любая другая частица, характеризуется энергией, массой и импульсом. Выражения (205.1), (205.2) и (200.2) связывают корпускулярные характеристики фотона — массу, импульс и энергию — с волновой характеристикой света — его частотой n.

Если фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление. Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.

Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на поверхность тела потоком монохроматического излучения (частота n), падающего перпендикулярно поверхности. Если в единицу времени на единицу площади поверх­ности тела падает N фотонов, то при коэффициенте отражения r света от поверхности тела rN фотонов отразится, а (1–r)N — поглотится. Каждый поглощенный фотон передаст поверхности импульс p_g=hn/c, а каждый отраженный — 2p_g=2hn/c (при от­ражении импульс фотона изменяется на –p_g). Давление света на поверхность равно импульсу, который передают поверхности в 1 с N фотонов:

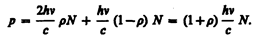
Nhn=E_e есть энергия всех фотонов, падающих на единицу поверхности в единицу времени, т. е. энергетическая освещенность поверхности (см. § 168), a E_e/c=w — объ­емная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность,

(205.3)

Формула (205.3), выведенная на основе квантовых представлений, совпадает с выра­жением, получаемым из электромагнитной (волновой) теории Максвелла (см. § 163). Таким образом, давление света одинаково успешно объясняется и волновой, и кван­товой теорией. Как уже говорилось (см. § 163), экспериментальное доказательство существования светового давления на твердые тела и газы дано в опытах П. И. Лебедева, сыгравших в свое время большую роль в утверждении теории Макс­велла. Лебедев использовал легкий подвес на тонкой нити, по краям которого прикреп­лены легкие крылышки, одни из которых зачернены, а поверхности других зеркальные. Для исключения конвекции и радиометрического эффекта (см. § 49) использовалась подвижная система зеркал, позволяющая направлять свет на обе поверхности крылы­шек, подвес помещался в откачанный баллон, крылышки подбиралась очень тонкими (чтобы температура обеих поверхностей была одинакова). Световое давление на кры­лышки определялось по углу закручивания нити подвеса и совпадало с теоретически рассчитанным. В частности оказалось, что давление света на зеркальную поверхность вдвое больше, чем на зачерненную (см. (205.3)).

§ 206. Эффект Комптона и его элементарная теория

Наиболее полно корпускулярные свойства света проявляются в эффекте Компто­на. Американский физик А. Комптон (1892—1962), исследуя в 1923 г. рассеяние мо­нохроматического рентгеновского излучения веществами с легкими атомами (пара­фин, бор), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также более длинноволновое излучение. Опыты показали, что разность Dl=l'–l не зависит от длины волны l падающего излучения и природы рассеивающего вещества, а определяется только углом рассея­ния q:

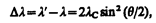(206.1)

где l' — длина волны рассеянного излучения, l_С —комптоновская длина волны (при рассеянии фотона на электроне l_С= 2,426 пм).

Эффектом Комптона называется упругое рассеяние коротковолнового электромаг­нитного излучения (рентгеновского и g-излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна: под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.

Объяснение эффекта Комптона дано на основе квантовых представлений о природе света. Если считать, как это делает квантовая теория, что излучение имеет кор­пускулярную природу, т. е. представляет собой поток фотонов, то эффект Комп­тона — результат упругого столкновения рентгеновских фотонов со свободными элек­тронами вещества (для легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными). В процессе этого столкновения фотон переда­ет электрону часть своих энергии и импульса в соответствии с законами их сохранения.

Рассмотрим упругое столкновение двух частиц (рис. 291) — налетающего фотона, обладающего импульсом p_g = hn/c и энергией e_g=hn, с покоящимся свободным электро­ном (энергия покоя W₀=m₀c²; т₀—масса покоя электрона). Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы со­хранения энергии и импульса.

Согласно закону сохранения энергии,

(206.2)

а согласно закону сохранения импульса,

(206.3)

где W₀=m₀c² — энергия электрона до столкновения, e_g=hn — энергия налетающего фотона, W= 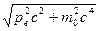— энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем случае значитель­на), — энергия рассеянного фотона. Подставив в выражение (206.2) значения величин и представив (206.3) в соответствии с рис. 291, получим