
ј“≈√ќ–»»:
јстрономи€Ѕиологи€√еографи€ƒругие €зыкиƒругое»нформатика»стори€ ультураЋитератураЋогикаћатематикаћедицинаћеханикаќбразованиеќхрана трудаѕедагогикаѕолитикаѕравоѕсихологи€–иторика—оциологи€—порт—троительство“ехнолог舑изика‘илософ舑инансы’им舄ерчениеЁкологи€ЁкономикаЁлектроника
ќбобщенные —-грамматики и приведение их к удлин€ющей
‘орме
—-грамматика называетс€ обобщенной, если она содержит аннулирующие правила (e - правила), то есть правила вида AЃ e , где e - пуста€ цепочка. ќбобщенна€ грамматика зачастую более проста и нагл€дна. “ем не менее следует помнить, что дл€ любой обобщенной —-грамматики существует эквивалентна€ неукорачивающа€ —-грамматика.
“еорема 4.6. ажда€ —-грамматика приводима к виду не более чем с одним аннулирующим правилом SЃ e , которого может и не быть.
ƒоказательство. ѕроведем его, как обычно, конструктивно, построением неукорачивающей грамматики.
¬о-первых, нужно определить, порождает ли исходна€ грамматика пустую цепочку. ѕусть S - начальный символ исходной грамматики G. ќпределим в G множество нетерминалов X i , из которых пустую цепочку можно получить за i шагов, и множество новых нетерминалов Zi. “аким образом мы определим аннулирующие нетерминалы.
X0 = { A | $ AЃ e } , Z0 = X0
X1 = { A | $ AЃ x , где xÎ X0 } , Z1 = X1\ X0
....................................................................
X i = { A | $ AЃ x , где xÎ 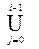 X j } , Z i = X i\ X i-1
X j } , Z i = X i\ X i-1
Ќа каком-то шаге Z i станет равным Æ и процесс формировани€ аннулирующих нетерминалов можно закончить. ≈сли S Ï X j, где  , то e Ï L(G) и правила SЃ e добавл€ть не надо. ¬ противном случае, заменим в исходной грамматике во всех правилах S на S1 , введем новый исходный нетерминал S и к правилам грамматики G добавим правила SЃ e ½S1.
, то e Ï L(G) и правила SЃ e добавл€ть не надо. ¬ противном случае, заменим в исходной грамматике во всех правилах S на S1 , введем новый исходный нетерминал S и к правилам грамматики G добавим правила SЃ e ½S1.
¬се остальные правила вида AЃ e можно удалить. ƒл€ этого заменим каждое из правил, правые части которых содержат хот€ бы по одному аннулирующему нетерминалу, множеством новых правил. ≈сли права€ часть правила содержит k вхождений аннулирующих нетерминалов, то множество, замен€ющее это правило, будет состо€ть из 2k правил, соответствующих всем возможным способам удалени€ некоторых (или всех) из этих вхождений.
ѕусть имеетс€ правило
BЃ j 1 A 1 j 2 A 2 j 3 ... j k A k j k+1 ,
где A i (  ) - аннулирующие нетерминалы. ƒобавим к этому правилу следующие правила:
) - аннулирующие нетерминалы. ƒобавим к этому правилу следующие правила:
BЃ j 1 j 2 A 2 j 3 ... j k A k j k+1 , удалено A 1
BЃ j 1 A 1 j 2 j 3 ... j k A k j k+1 , удалено A 2
..................................
BЃ j 1 A 1 j 2 A 2 j 3 ... j k j k+1 , удалено A k
BЃ j 1 j 2 j 3 ... j k A k j k+1 , удалены A 1, A 2
..................................
BЃ j 1 j 2 j 3 ... j k j k+1 , удалены A 1, A 2, ... A k .
«аметим, что в случае неоднозначности, на этом шаге может получитьс€ меньше чем 2k правил. “ак, дл€ аннулирующего нетерминала A, правило BЃ aAA будет замен€тьс€ трем€ правилами BЃ aAA½aA½a , так как в данном случае безразлично первое или второе вхождение A мы рассматриваем.
ѕосле такой замены правил дл€ всех правых частей исходной грамматики, содержащих аннулирующие нетерминалы, исключим из грамматики все e - правила, включа€ те, которые могли по€витьс€ при замене.
¬ результате мы получим грамматику, эквивалентную исходной, что доказываетс€ с использованием теорем 4.1 и 4.3.
ќтметим, что мы рассматривали случай, когда аннулирующие нетерминалы имеют и другие альтернативы, кроме перехода в пустую цепочку. ≈сли A Ѓ e единственна€ альтернатива нетерминала A, то правые части правил, содержащие его вхождение, можно просто исключить. ƒ
¬ результате применени€ рассмотренного алгоритма можно получить —-грамматику, по которой вывод любой непустой цепочки характеризуетс€ тем, что сентенциальна€ форма, получаема€ на каждом шаге вывода, будет не короче предыдущей. Ќе случайно полученна€ грамматика носит название неукорачивающей —-грамматики (Ќ —-грамматики).
ѕример 4.5. –ассмотрим обобщенную —-грамматику с аксиомой <число>.
<число> Ѓ <знак> <цел.часть> . <др.часть>
<знак> Ѓ +½-½e
<цел.часть> Ѓ <цел.часть><цифра>½e
<др.часть> Ѓ <цел.часть>
<цифра> Ѓ 0½1½...½8½9 и приведем ее к неукорачивающей форме.
¬начале покажем, что данна€ грамматика не порождает пустой цепочки. «десь
X0 = { <знак>, <цел.часть> },
X1 = { <др.часть> },
X2 = Æ и Z2 = Æ.
—реди множеств X - нет нетерминала <число> и, следовательно, правила
<число> Ѓ e добавл€ть не надо.
ѕроведем замены правил, правые части которых содержат аннулирующие нетерминалы, а затем удалим e - правила.
¬ результате получим грамматику
<число> Ѓ <знак> <цел.часть> . <др.часть>½<цел.часть> . <др.часть>½
<знак>. <др.часть>½<знак> <цел.часть> . ½ . <др.часть>½
<цел.часть> . ½<знак> . ½.
<цел.часть> Ѓ <цел.часть><цифра>½<цифра>
<др.часть> Ѓ <цел.часть>
<цифра> Ѓ 0½1½...½8½9
Ќа рис. 4.2 представлены деревь€ вывода цепочки +.9 по исходной (рис. 4.2 (а)) и результирующей (рис. 4.2 (б)) грамматикам.
ƒл€ приведени€ грамматики к удлин€ющей форме необходимо кроме аннулирующих правил исключить и цепные правила. ÷епное правило - это правило вида AЃ B , где A, B Î N.
“еорема 4.7. ƒл€ любой —-грамматики существует эквивалентна€ ей грамматика без цепных правил.
ƒоказательство. ѕусть в грамматике имеетс€ правило A Ѓ B и A ¹ S (A - не начальный символ грамматики). “огда все правила вида C Ѓ aAb заменим на правила C Ѓ aBb, а правила A Ѓ B удалим. ≈сли A = S и дл€ B существуют правила B Ѓ j 1½...½j n , то заменим их на S Ѓ j 1½...½j n , после чего S Ѓ B удалим.
Ћюбое такое преобразование правил допустимо исход€ из теорем 4.1 - 4.3 и устран€ет правила вида A Ѓ B. ѕовтор€ем такие преобразовани€ до тех пор, пока в грамматике не останетс€ цепных правил. š
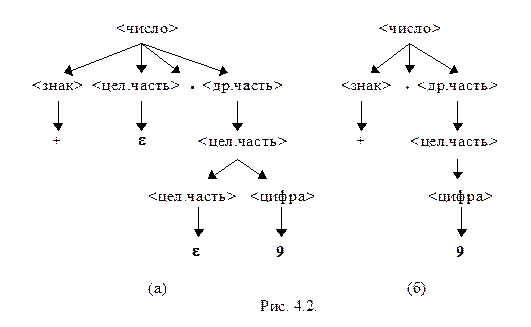 š
š
¬ результате устранени€ аннулирующих и цепных правил получаетс€ грамматика в удлин€ющей форме, где сентенциальна€ форма на каждом шаге вывода будет длиннее сентенциальной формы на предыдущем шаге. Ќапомним, что эта форма грамматики использовалась дл€ доказательства теоремы о разрешимости контекстных €зыков (теорема 1.1).
ѕример 4.6. ѕусть дана —-грамматика с правилами
S Ѓ aBa
B Ѓ A½Bc
A Ѓ aA½bb .
ѕравило B Ѓ A можно устранить, воспользовавшись результатами теоремы 4.2, и получить грамматику
S Ѓ aBa
B Ѓ aA½bb½Bc
A Ѓ aA½bb š
—-грамматика G=(N,S,P,S) называетс€ грамматикой без циклов, если в ней нет выводов A Þ+ A дл€ AÎ N. —-грамматика G называетс€ приведенной, если она без циклов, без аннулирующих правил и без тупиков.
√рамматики с e- правилами и циклами иногда труднее анализировать, чем грамматики без таковых. роме того, в любой практической ситуации тупики (бесполезные символы) без необходимости увеличивают объем анализатора. ѕоэтому дл€ некоторых алгоритмов синтаксического анализа, рассматриваемых во второй части пособи€, мы будем требовать, чтобы грамматики, фигурирующие в них, были приведенными. Ёто требование позвол€ет рассматривать все —-€зыки.
“еорема 4.8. ≈сли L - —-€зык, то L=L(G) дл€ некоторой приведенной —-грамматики G.
ƒоказательство. ѕрименить к —-грамматике, определ€ющей €зык L, эквивалентные преобразовани€ по теоремам 4.5 - 4.7. Ш
ƒата добавлени€: 2014-11-13; просмотров: 652; ћы поможем в написании вашей работы!; Ќарушение авторских прав |