
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
МЕХАНИЗМОВ
Провести анализ показателей качества исходной и синтезированной систем.
Для линейной системы:
1) определить показатели качества переходного процесса исходной и синтезированной систем:
- контура напряжения (тока);
- контура скорости;
2) определить кинематическую ошибку в режиме изменения управляющего воздействия с постоянной скоростью.
В пояснительной записке дать распечатку графиков процессов по пп.1, 2.
Для нелинейного контура напряжения (тока):
1) определить показатели качества переходного процесса синтезированного контура с нелинейным элементом;
2) определить параметры автоколебаний (если они имеют место).
В пояснительной записке дать распечатку графиков процессов по пп.1, 2.
Исследование САУ рекомендуется выполнить в среде MATLAB с применением пакета визуального моделирования SIMULINK. Возможно также использование других систем для исследования САУ.
 Литература.
Литература.
1. Бесекерский В.А., Попов Е.П. Синтез систем автоматического регулирования. - М.: Наука, 1972. – 326 с.
2. Сборник задач по теории автоматического управления и регулирования / В.А. Бесекерский, А.Н. Герасимов, С.В. Лучко; Под ред. Е.П. Попова. - М.: Высш. шк., 1978. – 240 с.
3. Проектирование инвариантных следящих приводов/ В.Н. Яворский, А.А. Бессонов, А.И. Коротаев и др.; Под ред. В.Н. Яворского. - М.: Высш. шк., 1963. – 420 с.
4. Автоматизированное проектирование систем автоматического управления / Я.Я. Алексанкин, А.Э. Боржовский, В.А. Жданов и др.; Под ред. В.В. Солодовникова. - М.: Машиностроение, 1989. – 244 c.
КИНЕМАТИЧЕСКИЙ И СИЛОВОЙ
АНАЛИЗ КРИВОШИПНО-ПОЛЗУННЫХ
МЕХАНИЗМОВ
Учебное пособие для
выполнения курсового проекта
(работы) по курсу
«Теория механизмов и машин»
Казань 2008
ОГЛАВЛЕНИЕ
Введение………………………………………………………………..…….….3
1. Кинематический синтез механизма и определение
характерных точек положения ползуна………………………….…………..….5
2. Кинематический анализ механизма…………………...………….…….6
2.1 Аналитический метод расчета…………………………………….……6
2.2 Графоаналитический метод определения кинематических
параметров……………………………………………….……………………….10
2.2.1. Определение положений …………………………………………....10
2.2.2. Определение скоростей……………………………………………...11
2.2.3. Определение ускорений……………………………………………..14
3. Силовой анализ механизма……………………………………………...16
3.1 Силовой анализ без учёта сил трения, зависящих
от сил, действующих в кинематических парах…………………………….….17
3.1.1 Графоаналитический метод силового анализа механизма.………..17
3.1.2 Определение уравновешивающего момента
методом возможных перемещений………………………………………….....24
3.1.3 Определение уравновешивающего момента с помощью
рычага Жуковского……………………………………………………………...25
4. Расчёт на ЭВМ…………………………………………………………...27
4.1. Кинематический и силовой анализ КПМ без учета сил
трения, зависящих от сил, действующих кинематических парах…………....28
4.1.1. Исходные данные……………………………………………………28
4.1.2. Результаты расчёта……………………………………………….….29
4.1.3. Кинематический анализ……………………………………….….....30
4.1.4. Определение силовых характеристик……………………………...30
4.2. Силовой анализ с учётом трения, зависящего от сил
в кинематических парах………………………………………………………...33
4.2.1. Методика расчёта…………………………………………………....34
4.2.2. Расчёт на ПК по программе А2Т…………………………………...37
5. Оформление курсовой работы……………………………………….…40
Заключение………………………………………………………………………40
Приложения………………………………………………………………….…..41
Список литературы………………………………………………………...……44
В В Е Д Е Н И Е
Задачи, которые должны быть решены при проектировании, определяются техническим заданием с прилагаемыми к нему техническими условиями, определяющими необходимые параметры, которые должны быть выдержаны при проектировании.
В курсовом проекте (работе) технические условия даются в задании, выдаваемом студенту. Ниже приводятся техническое задание на выполнение работы и технические условия в виде образца задания.
Техническое задание
1. Выполнить кинематический синтез схемы центрального кривошипно- ползунного механизма (КПМ) по заданным техническим условиям, включающим структурную схему механизма, и определить координаты характерных точек положения ползуна.
2. Провести кинематический анализ полученной схемы аналитическим и графоаналитическим методами.
3. Провести силовой анализ полученной схемы без учета составляющих сил трения, зависящих от величины усилий, действующих в кинематических парах, аналитическим и графоаналитическим методами.
4. Определить величину уравновешивающего момента с использованием принципа возможных перемещений аналитическим и графоаналитическим методами.
Кинематический и силовой анализ полученной схемы КПМ может быть проведен с использованием персонального компьютера (ПК) типа РС. Расчеты на ПК проводятся по готовым программам, составленным на алгоритмическом языке ФОРТРАН. В пособии даны указания по вводу исходных данных и расшифровки результатов расчета. В данном пособии силовой анализ КПМ с использованием ПК изложен в двух вариантах. В первом учитываются лишь постоянные составляющие сил трения, а во втором варианте – и силы трения, зависящие от усилий, действующих в кинематических парах.
При использовании ПК техническое задание дополняется следующими требованиями.
1. Построить годографы сил, действующих в кинематических парах, с учетом составляющих сил трения, зависящих от действующих в них усилий.
2. Построить графики законов движения 2-го и 3-го звеньев механизма в функции угла поворота начального звена.
3. Построить график уравновешивающего момента и сил, действующих в поступательной паре.
Образец задания
Механизм на рис. В1 представляет собой центральный КПМ, преобразующий вращательное движение кривошипа 1 в возвратно-поступательное движение ползуна 3.
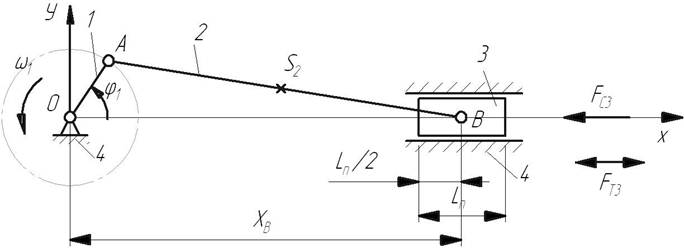
Рис. В1. Схема кривошипно-ползунного механизма
Механизм имеет следующие исходные данные:
1. Ход поршня 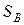 =0,35 м.
=0,35 м.
2. Длина поршня 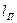 =0,22 м.
=0,22 м.
3. Длина шатуна АВ 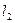 =1,4 м.
=1,4 м.  .
.
4. Частота вращения кривошипа  =120 об/мин.
=120 об/мин.
5. Масса шатуна 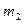 =7 кг.
=7 кг.
6. Масса поршня 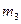 =10,5 кг.
=10,5 кг.
7. Перегрузка горизонтальная 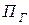 =1,0.
=1,0.
8. Постоянная сила трения в уплотнениях при движении поршня  =60 Н.
=60 Н.
9. Сила сопротивления, действующая на поршень:
при 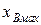 300 Н.
300 Н.
при 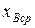 300 Н.
300 Н.
при 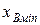 300 Н.
300 Н.
10. Радиус цапфы r =0.02 м.
11. Коэффициент трения в цапфе f=0,25.
12. Коэффициент трения в поступательной кинематической паре 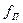 =0,2.
=0,2.
1.КИНЕМАТИЧЕСКИЙ СИНТЕЗ МЕХАНИЗМА И ОПРЕДЕЛЕНИЕ ХАРАКТЕРНЫХ ТОЧЕК ПОЛОЖЕНИЯ ПОЛЗУНА
По известным данным – ходу поршня 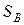 и длине шатуна
и длине шатуна 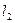 - необходимо определить длину кривошипа
- необходимо определить длину кривошипа 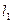 , а также координаты двух крайних и среднего положений поршня
, а также координаты двух крайних и среднего положений поршня 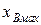 ,
, 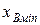 ,
, 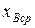 .
.
Очевидно, что:
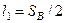 ; (1.1)
; (1.1)
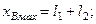 (1.2)
(1.2)
 (1.3)
(1.3)
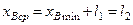 . (1.4)
. (1.4)
Для заданного механизма искомые значения параметров будут следующими:
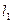 = 0,35/2 = 0,175 м;
= 0,35/2 = 0,175 м;
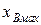 = (0,175 + 1,4) = 1,575 м;
= (0,175 + 1,4) = 1,575 м;
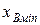 = (1,4 – 0,175) = 1,225 м;
= (1,4 – 0,175) = 1,225 м;
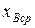 = 1,4 м.
= 1,4 м.
На рис. 1.1 представлена в масштабе схема механизма в восьми положениях через 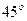 изменения угла
изменения угла 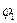 .На схеме показаны траектории движения точек А, В,
.На схеме показаны траектории движения точек А, В, 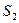 , где
, где 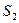 - центр тяжести звена 2.
- центр тяжести звена 2.
За начальное положение механизма принято положение , при котором кривошип расположен вдоль положительной полуоси 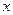 , т.е.
, т.е. 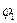 =0.
=0.
На рис. 1.1 указана дополнительная точка F, расположенная на оси  , с помощью которой задается признак сборки механизма. Координата
, с помощью которой задается признак сборки механизма. Координата 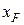 =+1 , если ползун слева от точки О кривошипа, и соответственно
=+1 , если ползун слева от точки О кривошипа, и соответственно 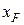 = -1 при правом расположении ползуна относительно кривошипа.
= -1 при правом расположении ползуна относительно кривошипа.
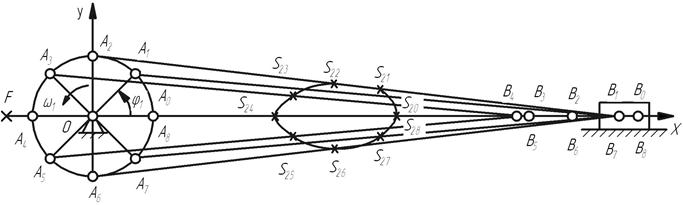
Рис. 1.1. Схема механизма в восьми положениях
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
Структурный анализ КПМ по Ассуру позволяет представить механизм в виде совокупности первичного механизма (ведущее звено 1 и стойка 4) и двухповодковой группы (звенья 2 и 3). Кинематический и силовой анализ механизма проводят в соответствии с его структурным составом.
Кинематический анализ КПМ может быть выполнен либо аналитическим , либо графоаналитическим методом.
Аналитическим методом для одного расчетного положения механизма определяются положения , скорости и ускорения звеньев 2 и 3, а также точки 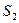 .
.
Графоаналитическим методом для того же расчетного положения механизма определяются его кинематические параметры с помощью планов положений механизма, скоростей и ускорений.
Кинематические параметры, полученные двумя способами, не должны отличаться друг от друга более чем на (5…10)%.
Расчетное положение механизма следует выбирать из рабочего диапазона его работы. Рабочий ход ползуна определяется движением его в направлении от точки О, то есть для сборки механизма, определяемой как  = -1 , рабочий ход соответствует диапазону перемещения ведущего звена от 180° до 360° , а для сборки
= -1 , рабочий ход соответствует диапазону перемещения ведущего звена от 180° до 360° , а для сборки  =+1 рабочий ход ползуна определяется диапазоном угла
=+1 рабочий ход ползуна определяется диапазоном угла 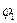 от 0 до180°. Таким образом, расчетным положениям механизма соответствуют углы
от 0 до180°. Таким образом, расчетным положениям механизма соответствуют углы 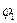 =
=  и
и 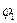 =
= 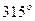 для
для 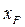 = -1 и углы
= -1 и углы 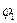 =
=  и
и 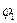 =
= 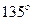 для
для 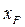 =+1.
=+1.
2.1.Аналитический метод расчета
Схема механизма в масштабе в расчетном положении ( 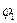 =315°) представлена на рис. 2.1, а.
=315°) представлена на рис. 2.1, а.
Из технического задания известны: длины звеньев 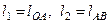 , угловая скорость начального звена ω1=const, расположение центра тяжести звена2–точки
, угловая скорость начального звена ω1=const, расположение центра тяжести звена2–точки 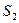 .
.
Необходимо определить кинематические параметры звеньев 2 и 3 в функции положения ведущего звена 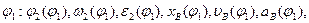 а также закон движения точки
а также закон движения точки 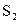 :
: 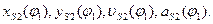
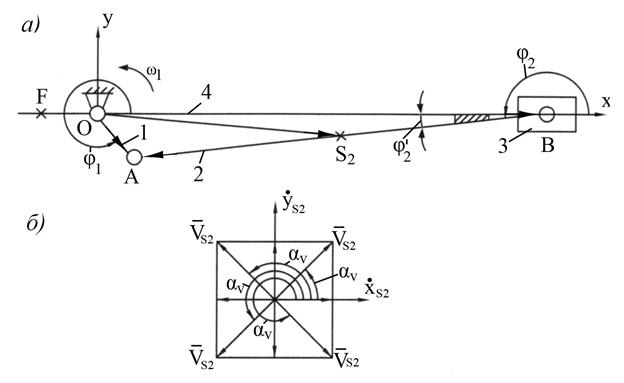
Рис. 2.1. Схема механизма в расчетном положении и определение положения
вектора скорости
Для решения задачи воспользуемся методом замкнутых векторных контуров.
Для этого вдоль каждого звена, составляющего замкнутый контур, направляется вектор. Его угловое положение определяется углом, положительное направление которого отсчитывается в направлении против часовой стрелки от положительной полуоси абсцисс.
На рис. 2.1,а показаны направления векторов треугольника ОВА.
Векторное уравнение замкнутого треугольника имеет вид
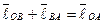 (2.1)
(2.1)
Спроектируем векторное уравнение на оси координат х и у
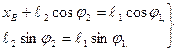 (2.2)
(2.2)
Из второго уравнения можно определить угол 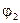 . Для принятых расчетных положений механизма он будет
. Для принятых расчетных положений механизма он будет
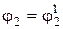 при
при 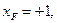
 при
при 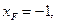 (2.3) где
(2.3) где 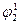 - острый угол, определяемый из треугольника ОАВ:
- острый угол, определяемый из треугольника ОАВ:
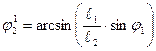 ; (2.4)
; (2.4)
Из первого уравнения системы определяется координата точки В
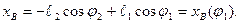 (2.5)
(2.5)
Для определения скоростей звеньев 2 и 3 продифференцируем систему двух уравнений по времени
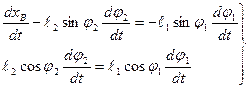 (2.6)
(2.6)
Или с учетом равенств
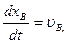
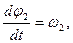
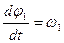 , где
, где 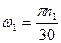 ,
,
будем иметь систему
 (2.7)
(2.7)
Из второго уравнения системы уравнений получим выражение для 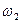 , а из первого – для
, а из первого – для 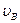 :
:
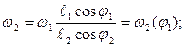 (2.8)
(2.8)
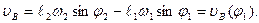 (2.9)
(2.9)
Повторное дифференцирование системы уравнений позволяет получить выражения для ускорений звеньев 2 и 3. С учетом равенств

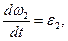
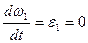
эти выражения имеют вид
 (2.10)
(2.10)
 (2.11)
(2.11)
Численные значения кинематических параметров для расчетного положения заданного механизма будут следующими:
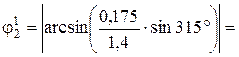
 ;
;
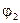 =
= 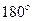 +
+  =
= 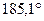 .
.
В радианной мере
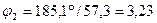 рад;
рад;
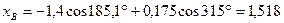 м;
м;
 1/с;
1/с;
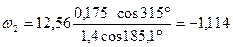 1/с;
1/с;
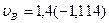
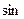
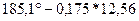
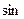
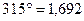 м/с;
м/с;
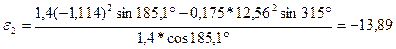
 ;
;
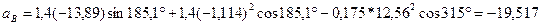
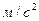 .
.
Для определения закона движения центра тяжести звена 2 – точки 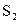 составим новый замкнутый векторный контур
составим новый замкнутый векторный контур 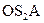 (рис. 2.1). Векторное уравнение его имеет вид:
(рис. 2.1). Векторное уравнение его имеет вид:
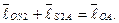 (2.12)
(2.12)
Проектируя уравнение на оси координат, получим координаты точки S2
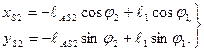 (2.13)
(2.13)
Первая и вторая производные от 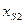 и
и 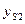 по времени дадут значения составляющих скорости и ускорения точки
по времени дадут значения составляющих скорости и ускорения точки 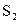
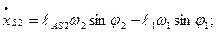 (2.14)
(2.14)
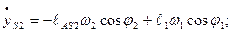 (2.15)
(2.15)
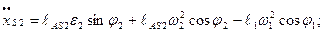 (2.16)
(2.16)
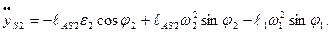 (2.17)
(2.17)
Значения полных векторов скорости и ускорения точки 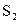 будут
будут
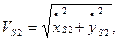 (2.18)
(2.18)
 (2.19)
(2.19)
Положение вектора скорости относительно оси 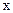 определяется углом αV (рис. 2.1,б):
определяется углом αV (рис. 2.1,б):
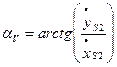 при
при  (2.20)
(2.20)
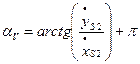 при
при 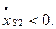
Аналогично определяется положение вектора ускорения:
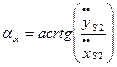 при
при  (2.21)
(2.21)
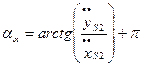 при
при 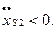
Подстановка в полученные выражения численных значений параметров заданного примера дает следующее результаты:
 м;
м;
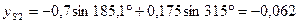 м;
м;
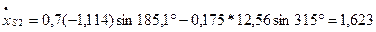 м/с;
м/с;
 м/с;
м/с;
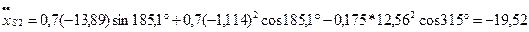
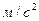 ;
;
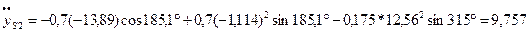
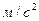 ;
;
 м/с;
м/с;
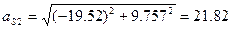
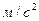 ;
;
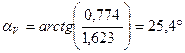 ;
;
 .
.
2.2.Графоаналитический метод определения кинематических параметров
Графические методы кинематического исследования механизмов обладают наглядностью, удобством контроля.
Графоаналитический метод определения кинематических параметров механизмов сводится к построению планов их положений, скоростей и ускорений.
2.2.1. Определение положений
План положений механизма – это графическое изображение взаимного расположения звеньев, соответствующее выбранному расчетному положению начального звена.
План положений механизма для угла 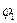 =
= 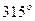 показан на рис. 2.1. Масштабный коэффициент плана положений
показан на рис. 2.1. Масштабный коэффициент плана положений  определяется как
определяется как
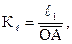 (2.22)
(2.22)
где 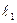 - действительная длина звена 1;
- действительная длина звена 1; 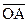 - длина отрезка, изображающего звено 1 на плане положений.
- длина отрезка, изображающего звено 1 на плане положений.
Тогда отрезок  , соответствующий длине звена 2, будет
, соответствующий длине звена 2, будет
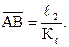 (2.23)
(2.23)
План положений позволяет определить угол 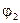 и координаты точек
и координаты точек 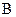 и
и 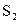 :
:
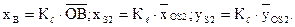 (2.24)
(2.24)
Для рассматриваемого примера численные значения приведенных параметров будут следующие:
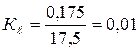 м/мм;
м/мм;
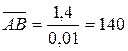 мм;
мм;
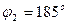 ;
; 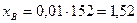 м;
м; 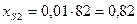 м;
м;  м.
м.
Значения 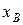 ,
, 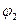 ,
, 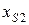 ,
, 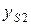 с большой степенью точности приближены к значениям, полученным аналитическим способом.
с большой степенью точности приближены к значениям, полученным аналитическим способом.
2.2.2. Определение скоростей
Метод основан на графическом решении векторных уравнений движения. Для построения плана скоростей должна быть известна кинематическая схема механизма, построенная в масштабе (рис. 2.2, а), и задан закон движения начального звена (например, 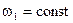 ).
).
Требуется найти линейные скорости точек  ,
, 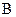 и
и 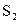 , а также угловую скорость звена 2.
, а также угловую скорость звена 2.
Построение плана скоростей начинается с определения скорости точки  кривошипа
кривошипа
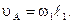 (2.25)
(2.25)
Вектор скорости точки  направлен перпендикулярно кривошипу
направлен перпендикулярно кривошипу  в направлении его вращения.
в направлении его вращения.
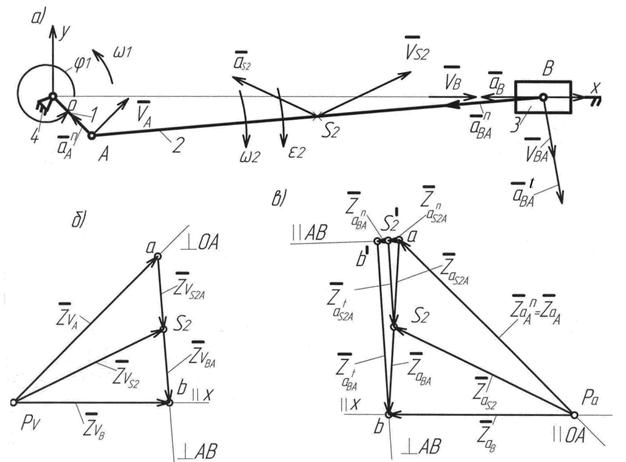
Рис.2.2. Схема механизма, планы скоростей и ускорений
Скорость точки  , принадлежащей звену 2, можно представить как векторную сумму скоростей переносного
, принадлежащей звену 2, можно представить как векторную сумму скоростей переносного  и относительного
и относительного  движений
движений
 (2.26)
(2.26)
Переносным движением звена 2 является поступательное движение его со скоростью точки 
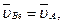
а относительным – вращательное движение звена 2 вокруг точки А. Если обозначить относительную скорость через 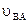 , то
, то

Окончательно векторное уравнение для скорости точки В будет иметь вид
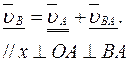 (2.27)
(2.27)
В этом уравнении векторы скоростей, известные по величине и направлению, подчеркнуты двумя чертами, а известные лишь по направлению – одной чертой.
Для определения указанных неизвестных величин строим план скоростей с выбранным масштабным коэффициентом 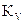
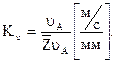 (2.28)
(2.28)
Здесь
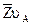 - длина отрезка, изображающего на плане скорость
- длина отрезка, изображающего на плане скорость 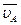 .
.
Из произвольной точки полюса плана скоростей  (рис. 2.2, б) проведем вектор
(рис. 2.2, б) проведем вектор 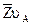 , перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости
, перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости 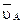 . Из конца вектора
. Из конца вектора 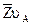 (точка а) проводим линию в направлении относительной скорости
(точка а) проводим линию в направлении относительной скорости 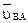 , перпендикулярную
, перпендикулярную 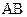 , а из полюса
, а из полюса 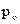 - линию в направлении скорости
- линию в направлении скорости 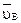 , параллельную
, параллельную 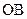 . В пересечении указанных линий находим точку b. Вектор
. В пересечении указанных линий находим точку b. Вектор 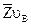 изображает скорость
изображает скорость 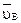 точки В, а вектор
точки В, а вектор 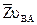 - скорость
- скорость 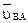 . Величины действительных скоростей определяют по формулам
. Величины действительных скоростей определяют по формулам

Направление скорости 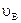 определяется при параллельном переносе вектора
определяется при параллельном переносе вектора 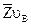 в точку В механизма (рис. 2.2, а). Т.к. вектор
в точку В механизма (рис. 2.2, а). Т.к. вектор 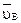 в точке В механизма направлен в сторону положительной полуоси
в точке В механизма направлен в сторону положительной полуоси 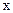 , знак скорости
, знак скорости 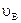 будет положительным.
будет положительным.
Модуль угловой скорости звена 2 будет
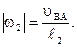 (2.29)
(2.29)
Направление 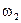 находится по вектору
находится по вектору 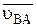 . На рис. 2.2, а
. На рис. 2.2, а 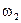 направлена по часовой стрелке.
направлена по часовой стрелке.
Скорость точки 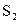 определяется с помощью векторного уравнения:
определяется с помощью векторного уравнения:
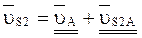 (2.30)
(2.30)
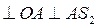
Здесь скорость относительного движения точки 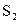
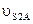 находится методом пропорционального деления отрезка ав на плане скоростей, изображающего относительную скорость
находится методом пропорционального деления отрезка ав на плане скоростей, изображающего относительную скорость 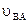
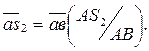 (2.31)
(2.31)
Действительная скорость 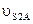 определяется как
определяется как
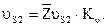 (2.32)
(2.32)
Для рассматриваемого примера численное значение скорости 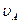 равно
равно
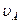 =12,56*0,175=2,198 м/с
=12,56*0,175=2,198 м/с 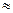 2,2 м/с.
2,2 м/с.
Если на плане скоростей (рис.2.2,б) известную скорость 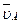 изобразить отрезком длиной 66 мм, то получим:
изобразить отрезком длиной 66 мм, то получим:
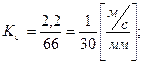
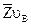 =51 мм;
=51 мм; 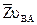 =47 мм;
=47 мм;
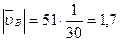 м/с.
м/с.
Так как вектор 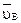 в точке В механизма направлен в сторону положительной полуоси
в точке В механизма направлен в сторону положительной полуоси 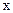 ,знак будет положительным:
,знак будет положительным:
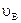 =1,7 м/с
=1,7 м/с
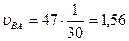 м/с;
м/с; 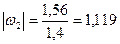
 .
.
Угловая скорость 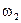 направлена по часовой стрелке, поэтому имеет знак «минус»:
направлена по часовой стрелке, поэтому имеет знак «минус»:
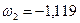 1/с;
1/с;
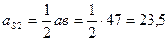 мм;
мм; 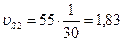 м/с.
м/с.
Сравнение с результатами аналитического метода расчета дает ошибку не более 3%.
2.2.3. Определение ускорений
Построение плана ускорений позволяет определить линейные ускорения точек  ,
,  и
и 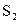 , а также угловое ускорение звена 2.
, а также угловое ускорение звена 2.
Ускорение точки  кривошипа складывается из суммы нормальной
кривошипа складывается из суммы нормальной 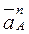 и тангенциальной
и тангенциальной 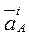 составляющих
составляющих
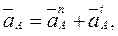 (2.33)
(2.33)
где 
Нормальные составляющие ускорений всегда направлены по радиусу к центру вращения, а тангенциальные составляющие перпендикулярны радиусу и направлены в сторону углового ускорения.
Ускорение точки В, принадлежащей звену 2, можно представить в виде векторной суммы ускорений переносного  и относительного
и относительного  движений
движений
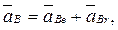 (2.34)
(2.34)
где 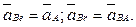
Относительное ускорение точки 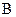 также состоит из двух составляющих
также состоит из двух составляющих
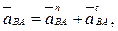 (2.35)
(2.35)
где 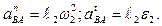
С учетом приведенных выше формул и в случае 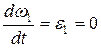 окончательно получим
окончательно получим 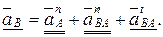 (2.36)
(2.36)
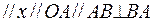
Как и раньше, одной чертой подчеркнуты векторы, известные только по направлению, а полностью известные векторы подчеркнуты двумя чертами.
Построение плана ускорений начинаем с выбора масштабного коэффициента плана ускорений 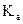 по любой известной величине – либо по
по любой известной величине – либо по  , либо по
, либо по 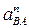 . Пусть
. Пусть
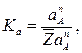 (2.37)
(2.37)
где  - длина отрезка, изображающего ускорение
- длина отрезка, изображающего ускорение 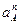 .
.
Тогда величина отрезка  , изображающего известное ускорение
, изображающего известное ускорение 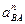 , будет
, будет
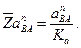 (2.38)
(2.38)
Из произвольной точки полюса плана ускорений 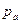 (рис. 2.2, в) откладываем отрезок
(рис. 2.2, в) откладываем отрезок  в направлении к центру вращения звена 1 – точке
в направлении к центру вращения звена 1 – точке 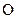 . Так как
. Так как 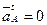 и, следовательно,
и, следовательно, 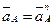 , отрезок
, отрезок 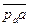 изображает полное ускорение точки
изображает полное ускорение точки  .
.
Из конца отрезка 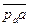 параллельно
параллельно 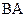 по направлению к центру относительного вращения звена 2 – точке
по направлению к центру относительного вращения звена 2 – точке  откладываем отрезок
откладываем отрезок  и из его конца перпендикулярно
и из его конца перпендикулярно 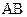 проводим линию действия тангенциальной составляющей относительного ускорения
проводим линию действия тангенциальной составляющей относительного ускорения 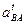 . Затем из полюса плана
. Затем из полюса плана 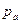 параллельно
параллельно 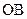 проводим линию действия абсолютного ускорения точки
проводим линию действия абсолютного ускорения точки 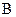 . Точка b, полученная на пересечении этих линий, определяет концы отрезков
. Точка b, полученная на пересечении этих линий, определяет концы отрезков 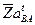 и
и 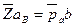 , изображающих соответствующие ускорения. Величины этих ускорений будут
, изображающих соответствующие ускорения. Величины этих ускорений будут
 и
и 
Так как вектор ускорения 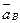 направлен в сторону отрицательной полуоси
направлен в сторону отрицательной полуоси 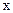 , то знак ускорения
, то знак ускорения 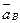 будет отрицательным.
будет отрицательным.
Соединив прямой точки  и b плана ускорений, получим отрезок
и b плана ускорений, получим отрезок 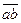 , изображающий полное относительное ускорение
, изображающий полное относительное ускорение 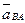 . Его величина будет
. Его величина будет
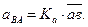
Величина углового ускорения звена 2 определяется из уравнения
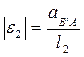 . (2.39)
. (2.39)
Перенеся вектор ускорения  в точку
в точку 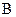 механизма и рассматривая движение точки В относительно точки
механизма и рассматривая движение точки В относительно точки  , можно определить направление ускорения
, можно определить направление ускорения 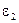
Ускорение точки 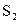 определяется из векторного уравнения
определяется из векторного уравнения
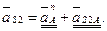 (2.40)
(2.40)

Величина относительного ускорения  находится аналогично скорости
находится аналогично скорости 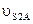 - методом пропорционального деления отрезка
- методом пропорционального деления отрезка 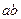 , изображающего относительное ускорение
, изображающего относительное ускорение 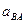
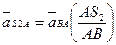 (2.41)
(2.41)
или на рис. 2.2, в
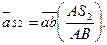
Полное ускорение точки S2 определяется как
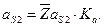 (2.42)
(2.42)
Для рассматриваемого примера расчеты дают следующие значения параметров:
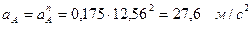 ;
;
 .
.
Возьмем отрезок 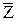 а
а 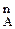 =82,8мм, тогда масштабный коэффициент будет равен
=82,8мм, тогда масштабный коэффициент будет равен 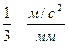
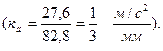
Отрезок, изображающий известное ускорение 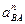 :
:
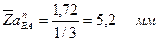 .
.
Искомые ускорения будут:
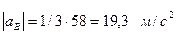 ;
;
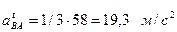 ;
;
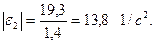
Так как вектор ускорения  направлен в сторону отрицательной полуоси
направлен в сторону отрицательной полуоси 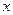 , то
, то
 .
.
Угловое ускорение  направлено по часовой стрелке, поэтому
направлено по часовой стрелке, поэтому
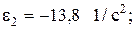

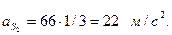
Сравнение результатов расчета со значениями, полученными аналитическим методом, дает максимальную ошибку не более 3%.
3. СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА
Задачей силового анализа рычажных механизмов является определение сил, действующих в кинематических парах механизма, уравновешивающей силы или уравновешивающего момента, которые надо приложить к ведущему звену для обеспечения требуемого закона движения ведомого звена.
Силовой расчет механизма в дальнейшем позволит решить следующие инженерные задачи: 1) расчет звеньев механизма на прочность, жесткость, износоустойчивость и т.п.; 2) расчет подвижных соединений звеньев на долговечность; 3) выбор мощности двигателя и т.д.
При проектировании механизма силовой анализ выполняется в два этапа. На первом этапе определяют силы в кинематических парах без учета сил трения, зависящих от усилий в кинематических парах, учитывая лишь постоянные составляющие, заданные в технических условиях.
Используя результаты первого этапа, определяют силы и моменты трения, зависящие от сил реакций, и на втором этапе с их учетом определяют истинные реакции в кинематических парах.
При использовании кинетостатического метода в уравнения равновесия, называемые уравнениями кинетостатики, входят не только внешние силы и моменты, силы в кинематических парах, но и силы и моменты сил инерции.
Для кинетостатической определимости плоский механизм не должен иметь избыточных связей.
Силовой расчет механизма проводят в соответствии с его структурным составом, т.е. расчет начинают со структурной группы, наиболее удаленной от начального звена, и заканчивают расчетом первичного механизма.
3.1 Силовой анализ без учета сил трения, зависящих от сил, действующих в кинематических парах.
Для первого этапа силового анализа проведем расчет несколькими методами:
1) для расчетного положения механизма графоаналитическим методом определим силы во всех кинематических парах и уравновешивающий момент, который необходимо приложить к начальному зевну ;
2) основываясь на методе возможных перемещений, определим аналитическим и графоаналитическим способами уравновешивающий момент для того же расчетного положения механизма.
3.1.1. Графоаналитический метод силового анализа механизма
Для расчетного положения механизма необходимо определить все силы и моменты сил, действующие на звенья механизма.
1. Силы тяжести
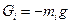 (
( 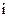 =2,3). (3.1)
=2,3). (3.1)
2. Силы от действия горизонтальной и вертикальной перегрузок:
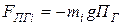 ,
, 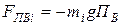 . (3.2)
. (3.2)
3. Главные векторы и главные моменты инерционных сил, к которым приводятся силы инерции, действующие на каждое звено механизма. Для звеньев 2 и 3

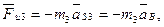 (3.3)
(3.3)
где 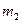 и
и 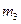 -массы звеньев 2 и 3;
-массы звеньев 2 и 3; 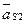 и
и  -ускорения центров масс звеньев (для звена 3 точка
-ускорения центров масс звеньев (для звена 3 точка 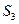 совпадают с точкой В);
совпадают с точкой В);  -угловое ускорение звена 2;
-угловое ускорение звена 2;  -момент инерции масс звена 2 относительно оси, проходящей через центр масс и перпендикулярной плоскости движения звена, который определяется по формуле
-момент инерции масс звена 2 относительно оси, проходящей через центр масс и перпендикулярной плоскости движения звена, который определяется по формуле
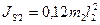 . (3.4)
. (3.4)
4. Сила трения на ползуне
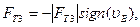 (3.5)
(3.5)
где 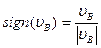 .
.
5. Сила сопротивления на ползуне:
для нерабочего хода ползуна 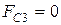 ;
;
для рабочего хода 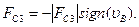 (3.6)
(3.6)
Здесь 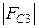 -модуль силы сопротивления, соответствующий расчетному положению механизма. Для определения значения этой силы необходимо построить приближенный график параболической зависимости силы сопротивления от координаты точки В
-модуль силы сопротивления, соответствующий расчетному положению механизма. Для определения значения этой силы необходимо построить приближенный график параболической зависимости силы сопротивления от координаты точки В 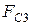 (
( 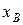 ) , используя три значения функции
) , используя три значения функции 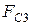 для трех значений аргумента
для трех значений аргумента 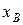 , данные в задании.
, данные в задании.
График зависимости 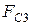 (
( 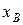 ) представлен на рис.3.1.
) представлен на рис.3.1.
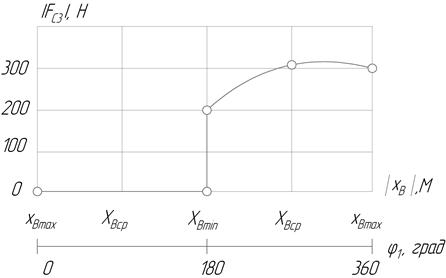
Рис. 3.1. Зависимость силы сопротивления от положения ползуна
Знак «минус» везде учитывает направление силового параметра, противоположное направлению соответствующего кинематического параметра.
Численные значения сил и моментов сил для расчетного положения рассматриваемого механизма ( 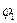 =
= 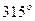 ) будут следующими:
) будут следующими:
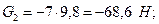
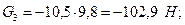
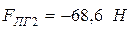 ;
; 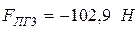 ;
; 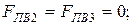
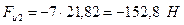 ;
; 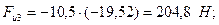
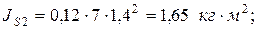
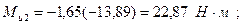
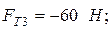
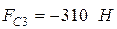 (см.рис.3.1);
(см.рис.3.1); 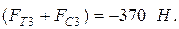
Малыми величинами, которые составляют не более (5…10)% от максимальной известной силы, можно пренебречь.
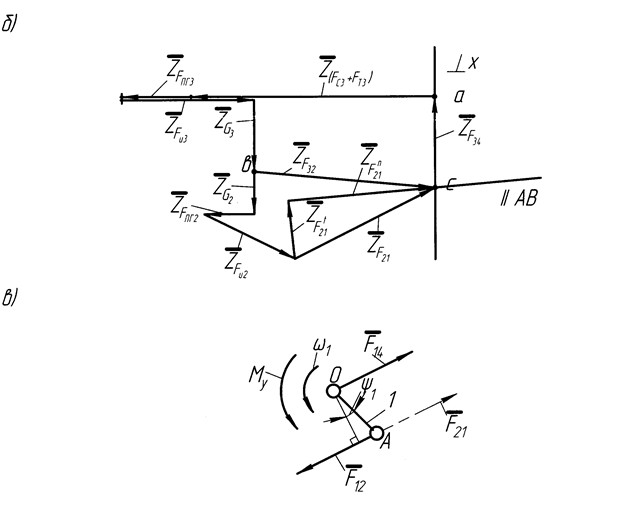
Силовой расчет механизма следует начать с двухповодковой группы, состоящей из звеньев 2 и 3. Схема структурной группы, изображенной в масштабе со всеми приложенными силами, представлена на рис. 3.2,а. Определению подлежат силы реакции  ,
, 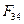 и
и  .
.
Задача нахождения сил и плеча  является статически определимой задачей, поскольку для группы из двух звеньев можно составить 6 уравнений равновесия, и определению подлежат 6 неизвестных - величины и направления сил реакций во вращательных кинематических парах А и В, величина и точка приложения силы
является статически определимой задачей, поскольку для группы из двух звеньев можно составить 6 уравнений равновесия, и определению подлежат 6 неизвестных - величины и направления сил реакций во вращательных кинематических парах А и В, величина и точка приложения силы 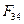 в поступательной кинематической паре ползун – неподвижные направляющие ползуна.
в поступательной кинематической паре ползун – неподвижные направляющие ползуна.
Для удобства проведения расчета главный момент сил инерции можно заменить парой сил, приложенных в точках А и В звена 2. Значения сил будут
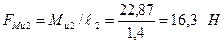 .
.
При графоаналитическом методе расчета следует неизвестную силу реакции  предоставить в виде двух составляющих: нормальной
предоставить в виде двух составляющих: нормальной 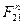 , направленной вдоль звена, и касательной
, направленной вдоль звена, и касательной 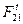 , направленной перпендикулярно звену.
, направленной перпендикулярно звену.
Все неизвестные силы реакции на рис. 3.2,а направлены произвольно. Если из расчета какая-либо сила получится со знаком «минус», это значит, что ее действительное направление противоположно принятому.
Для системы сил, действующих на звено 2, составим уравнение моментов относительно точки 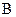
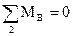 . (3.7)
. (3.7)
Если условиться, что моменты, направленные против часовой стрелки, считаются положительными, а по часовой стрелке - отрицательными, то уравнение моментов будет иметь вид
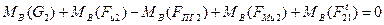 ,
,
где неизвестная составляющая силы 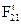 направлена произвольно – вниз от точки
направлена произвольно – вниз от точки  .
.
В развернутом виде уравнение перепишется как
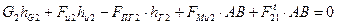 .
.
Откуда неизвестная сила 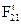 будет
будет
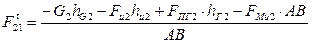 . (3.8)
. (3.8)

 точкой В);центров масс звеньев (для звена 3 точка ься сисилы во всех кинематических парах
точкой В);центров масс звеньев (для звена 3 точка ься сисилы во всех кинематических парах
Рис.3.2. Схема к кинетостатическому расчету двухповодковой группы,
ведущего звена и план сил
Здесь через  с индексами обозначены плечи соответствующих сил относительно точки
с индексами обозначены плечи соответствующих сил относительно точки 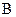 . Как видно из формулы для
. Как видно из формулы для 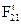 , плечи сил могут быть взяты непосредственно из рисунка группы (рис.3.2, а), невзирая на масштаб его построения.
, плечи сил могут быть взяты непосредственно из рисунка группы (рис.3.2, а), невзирая на масштаб его построения.
Следует отметить, что при определении численных значений сил реакций, как 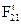 , так и других, все силы следует брать по модулю, так как знак силы указывает на ее действительное направление, а на схеме механизма знак силы был учтен при изображении ее на рисунке.
, так и других, все силы следует брать по модулю, так как знак силы указывает на ее действительное направление, а на схеме механизма знак силы был учтен при изображении ее на рисунке.
Численное значение касательной составляющей 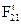 для рассматриваемого примера будет
для рассматриваемого примера будет
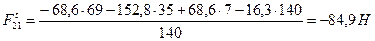 .
.
Знак «минус» означает, что сила 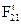 должна быть направлена в противоположную от выбранного направления сторону, т.е. от точки А вверх, что показано на рис. 3.2,а.
должна быть направлена в противоположную от выбранного направления сторону, т.е. от точки А вверх, что показано на рис. 3.2,а.
Для определения величин нормальной составляющей силы в точке 
 и силы
и силы 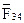 составим векторное уравнение равновесия структурной группы, сгруппировав силы по звеньям:
составим векторное уравнение равновесия структурной группы, сгруппировав силы по звеньям:
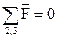 . (3.9)
. (3.9)
Или
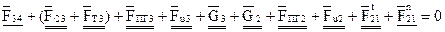 .
.

В уравнении силы, известные по величине и направлению, подчеркнуты двумя чертами, а известные лишь по направлению - одной чертой.
Решим векторное уравнение графически - путем построения многоугольника сил (рис.3.2,б). Для этого необходимо выбрать масштабный коэффициент построения плана сил 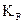 , используя любую известную силу, лучше максимальную : у нас
, используя любую известную силу, лучше максимальную : у нас 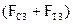 ,
,
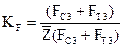 . (3.10)
. (3.10)
Если для рассматриваемого примера отрезок 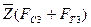 , изображающий сумму сил
, изображающий сумму сил 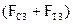 =370 Н, выбрать равным 74 мм, то масштабный коэффициент плана сил будет «удобным» числом:
=370 Н, выбрать равным 74 мм, то масштабный коэффициент плана сил будет «удобным» числом:

Тогда отрезки, изображающие остальные известные силы, будут
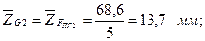
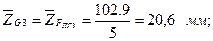
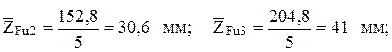
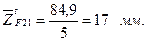
Построение силового многоугольника начнем с линии действия силы 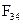 , перпендикулярной оси
, перпендикулярной оси 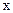 (рис. 3.2, б). Из произвольной точки а на этой линии, которая является точкой конца отрезка, изображающего вектор силы
(рис. 3.2, б). Из произвольной точки а на этой линии, которая является точкой конца отрезка, изображающего вектор силы  , проведем вектор
, проведем вектор 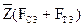 , известный по величине и направлению. Из конца этого вектора проведём следующий известный вектор
, известный по величине и направлению. Из конца этого вектора проведём следующий известный вектор 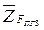 и так далее, согласно векторному уравнению сил. Из конца последнего известного вектора
и так далее, согласно векторному уравнению сил. Из конца последнего известного вектора 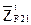 проводим линию действия силы
проводим линию действия силы 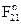 , параллельную
, параллельную 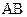 . Пересечение в точке с этой линии и первой, перпендикулярной оси
. Пересечение в точке с этой линии и первой, перпендикулярной оси 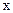 , определяет искомые отрезки
, определяет искомые отрезки  и
и  . Измерив их длины, определим значения сил:
. Измерив их длины, определим значения сил:
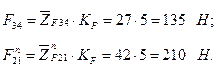
Полный вектор силы  равен геометрической сумме нормальной и касательной его
равен геометрической сумме нормальной и касательной его
Дата добавления: 2014-12-03; просмотров: 477; Мы поможем в написании вашей работы!; Нарушение авторских прав |