
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формалізація, алгоритмізація та автоматизована обробка економічної інформації
Підготовка реальних задач до автоматизованого розв’язування з використанням комп’ютера складається з наступних етапів:
І. Постановка задачі та її змістовий аналіз (створення інформаційної моделі задачі).
ІІ. Формалізація задачі (побудова математичної моделі, вибір методу розв’язування)
ІІІ. Складання алгоритму на основі вибраного методу.
IV. Запис програми.
V. Введення, налагодження, тестування програми.
VI. Виконання програми, аналіз результатів.
Формалізації будь-якого процесу, завдання чи задачі передує вивчення структури елементів, з яких складається цей процес, в результаті чого з’являється так званий змістовий опис процесу, тобто основа для створення формалізованої схеми процесу.
Змістовий опис включає в себе:
1. Аналіз умови задачі, а саме, що дано (тобто які величини є вхідними та які їх значення допустимі), що потрібно зробити (тобто, які величини будуть вихідними або результатом і в якому вигляді вони мають бути представлені).
2. Проводиться запис в аналітичній формі всіх співвідношень між вихідними величинами і вхідними, описуються логічні умови та дії щодо реалізації процесу розв’язання.
3. Описується сукупність дій, необхідних для розв’язування задачі, тобто записують алгоритм розв’язування задачі.
Під алгоритмом розуміють послідовність дій, які необхідно виконати над вхідними даними, щоб розв’язати задачу і отримати результат або досягти поставленої мети;
Алгоритм має такі властивості: дискретність, визначеність, зрозумілість, універсальність, скінченність, результативність, формальність. Якщо алгоритм відповідає переліченим властивостям, то його виконання здійснюється формально, і це можна доручити комп’ютерам.
Розробка алгоритму є складним і трудомістким процесом. Алгоритмізація – це техніка розробки (складання) алгоритму для вирішення завдань на комп’ютері.
Ефективним методом побудови алгоритму є метод покрокової деталізації, при якому завдання розбивається на кілька простих підзадач (модулів) і для кожного модуля створюється свій власний алгоритм. Здебільшого модуль реалізує певний процес обробки інформації і застосовується як окремо, так і для включення модуля в інший алгоритм.
Застосування модульності при створенні алгоритмів дозволяє розбити великі задачі на незалежні блоки (модулі), усуває повторення стандартних дій і значно прискорює процес відлагодження алгоритму в цілому. Найчастіше алгоритм складається з головного модуля, який містить декілька інших модулів, створених раніше. Використовуючи модулі як складові великої конструкції, можна створювати алгоритми будь–якого ступеня складності, і при цьому не втрачати контролю за функціюванням алгоритму всієї задачі. Такий метод називається структурованим проектуванням алгоритму „зверху донизу”, є універсальним і може використовуватися як для обчислювальних процесів (так зване системне програмування), так і для процесів реального життя.
Для запису алгоритму рішення задачі застосовуються наступні способи їх подання:
· Словесно- формульний опис
· Блок-схема (схема графічних символів)
· Алгоритмічні мови
· Операторні схеми
· Псевдокод
Для запису алгоритму існує загальна методика:
· Кожен алгоритм повинен мати ім'я, яке розкриває його сенс.
· Необхідно позначити початок і кінець алгоритму.
· Описати вхідні і вихідні дані.
· Вказати команди, які дозволяють виконувати певні дії над виділеними даними
Загальний вигляд алгоритму
· Алгоритм: Назва алгоритму
· Опис даних
· Початок
· Команди
· Кінець
Формульно-словесный спосіб запису алгоритму характеризується тим, що опис здійснюється за допомогою слів і формул. Вміст послідовності етапів виконання алгоритмів записується на природній професійній мові наочної області в довільній формі.
Графічний спосіб опису алгоритму (блок - схема) набув найбільшого поширення. Для графічного опису алгоритмів використовуються схеми алгоритмів або блокові символи (блоки), які з'єднуються між собою лініями зв'язку.
Кожен етап обчислювального процесу представляється геометричними фігурами (блоками). Вони діляться на арифметичні або обчислювальні (прямокутник), логічні (ромб) і блоки введення-виведення даних (паралелограм).
Основні елементи блок – схем.
 Початок алгоритму
Початок алгоритму
 Кінець алгоритму
Кінець алгоритму

Блоки введення даних та виведення результату

Блок виконання обчислень (для запису вказівки присвоєння)
 Блок прийняття рішень (розгалуження), для запису умови, що перевіряється
Блок прийняття рішень (розгалуження), для запису умови, що перевіряється

Блок модифікації, для повторного присвоєння нових значень параметру арифметичного циклу
 Блок виклику допоміжного алгоритму
Блок виклику допоміжного алгоритму
Порядок виконання етапів вказується стрілками, що з’єднують блоки. Геометричні фигури розміщують сгори до низу і зліва на право. Нумерація блоків здійснюється в порядку їх розміщення у схемі.
Базові структури алгоритмів. В 1966 році вчені Бром і Джакопіні довели наступну теорему: «Кожен алгоритм може бути побудований за допомогою лише трьох базових алгоритмічних структур – слідування, розгалуження, циклу».
Структура слідування, або лінійна, містить вказівки, що виконуються послідовно одна за одною.
Розгалужена структура передбачає вибір дії залежно від дотримання деякої умови, при цьому деякі вказівки можуть не виконуватися взагалі.
Умови, що використовуються в розгалуженому алгоритмі поділяються на прості і складені. Прості умови записують за допомогою двох виразів поєднаних знаками відношень >, <, >=, <=, =, <>. Результатом перевірки умови є логічний вираз ІСТИНА (TRUE), якщо умова виконується, або ХИБНІСТЬ (FALSE), якщо умова не виконується.
Складена умова містить дві і більше простих умов, поєднаних знаками логічних операцій:
· i, &, and, наприклад - <умова1> & <умова2>, and(умова1;умова2) – результат буде істинним тоді і тільки тоді, коли обидві прості умови будуть дотримані.
· або, or, наприклад - <умова1> or <умова2>, or(умова1;умова2) – результат буде істинним тоді, коли хоча б одна з умов буде дотримана.
· не, not, наприклад – not(умова1) – це є заперечення умови1, результатом буде твердження, протилежне умові1.
Таблиця 1.1.2
Таблиця істинності тверджень
| Умова1 | Умова2 | and(Умова1;Умова2) | Or(Умова1;Умова2) | Not(Умова1) |
| T | T | T | T | F |
| F | T | F | T | T |
| T | F | F | T | F |
| F | F | F | F | T |
Циклічна структура використовується при необхідності повторень виконання деяких дій з різними (новими) значеннями вхідних даних, тобто коли треба виконати перебір варіантів. Алгоритмі циклічної структури описують цикли трьох видів: безумовний або арифметичний цикл (цикл ДЛЯ); умовний цикл з передумовою (цикл ПОКИ) та умовний цикл з післяумовою (цикл ДО).
Як правило, умовні цикли використовують тоді, коли невідома кількість повторень вказівок циклу, такі цикли ще називають ітераційними.
Для побудови алгоритмів використовують структурний метод, що полягає в структурованому проектуванні алгоритму «зверху-донизу» та метод покрокової деталізації, коли завдання розбивають на кілька простих підзадач (модулів) і для кожної підзадачі (кожного модуля) створюють власний алгоритм, який можна використовувати як окремо, так і включаючи в інший алгоритм, один з яких є головним а інші допоміжні, або підалгоритми. Якщо у процесі обчислення допоміжний алгоритм використовують багаторазово, то його оформляють у вигляді алгоритму-процедури, або алгоритму-функції. Особливість їх використання полягає в тому, що результатом алгоритму-функції є тільки одне значення - значення описаної функції.
Комбінуючи базові структури алгоритмів, можна створювати алгоритми будь-якого ступеня складності.
Приклади алгоритмів. Алгоритм лінійної структури.
Знайти значення виразу:

для заданих вхідних значень а, с і х = cos(a2c2).
При формалізації поставленого завдання використовується метод покрокової деталізації і з'ясовується, що процес визначення Y розбивається на такі етапи:
1. Визначення вхідних значень змінних а, с.
2. Обчислення виразу х =cos(a2c2).
3. Обчислення виразу 
4. Виведення отриманих вихідних значень х та Y.
Блок-схема алгоритму розв’язування задачі:

Алгоритм розгалуженої структури. Приклад 1: Обчислити значення коренів квадратного рівняння:

При формалізації процес визначення коренів квадратного рівняння розбивається на такі етапи:
1. Уведення вхідних значень коефіцієнтів a, b і вільного члена с.
2. Визначення значення дискримінанта.
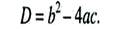
3. Перевірка отриманого значення дискримінанта: якщо дискримінант > 0, то можна продовжувати обчислення і визначати корені рівняння, в противному разі дійсних значень коренів немає.
4. Продовження обчислень — визначення коренів:

5. Виведення отриманих результатів: x1 та x2.
6. Виведення повідомлення
Дійсних коренів немає
у разі коли дискримінант < 0.
Алгоритм може виконуватися у порядку 1, 2, 3, 4, 5 пункти, якщо перевірка умови дає результат ИСТИНА, або у порядку 1, 2, 3, 6 пункти, якщо перевірка умови дає результат ЛОЖЬ
. 
У блок-схемі алгоритму блок № 4 використовується для перевірки умови і реалізує розгалуження: якщо умова набуває результату істина, далі алгоритм продовжується по блоках 5, 6, 7, 9, а блок 8 зовсім не використовується. Навпаки, коли умова набуває значення хиба, алгоритм продовжується по блоках 8, 9, при цьому блоки 5, 6, 7 не виконуються взагалі.
Приклад 2: Обчислити значення виразу:

При х > 12 та х = 4 функція не визначена.
Етапи розв'язання задачі:
1. Уведення коефіцієнтів а, Ь.
2. Уведення вхідного значення аргументу х.
3. Перевірка значення аргументу х:
· Якщо х = 2, то значення Y обчислюється за формулою

· Якщо х = 4, х < 2 або х > 12, то виводиться повідомлення, що функція не визначена.
· Якщо х > 8, то значення Y обчислюється за формулою:

· Якщо жодна з перерахованих вище умов не виконується, то значення Y обчислюється за формулою:

4. Виведення значення Y.
На третьому етапі алгоритм має містити розгалуження, яке реалізовує перевірку складної умови.
Блок-схема створеного алгоритму:

Алгоритм циклічної структури. Циклом називають повторення послідовної кількості кроків алгоритму.
Розрізняють такі основні види циклів:
• цикл по лічильнику;
• цикл по вхідному значенню;
• цикл по вихідному значенню (ітераційний цикл);
• цикл з накопиченням.
При кожному черговому виконанні циклу перевіряється умова на продовження роботи, і, якщо умова набуває результату ИСТИНА, цикл виконується, а якщо ж умова набуває результату ЛОЖЬ — цикл не виконується. Перевірка умови може бути організована на початку циклу, і такий цикл називається циклом з передумовою, або у кінці циклу — тоді такий цикл називається циклом з післяумовою.
Різниця між такими циклами полягає в тому, що цикл з післяумовою виконується хоча б один раз, а цикл з передумовою може не виконуватися жодного разу.
Цикл по лічильнику характерний тим, що заздалегідь відома кількість повторень циклу, і цикл буде виконуватися, доки значення лічильника циклу на перевищить зазначену кількість повторень.
Цикл по вхідному значенню характерний тим, що відомі початкове та кінцеве значення вхідної змінної, а також закон (формула), за яким значення вхідної змінної міняється від циклу до циклу. Цикл продовжує виконуватися, доки значення вхідної змінної лежатиме у межах від початкового до кінцевого значення, і кількість повторень циклу в явному вигляді невідома.
Цикл по вихідному значенню характерний тим, що він виконується, доки вихідне значення не досягне зазначеної величини, тобто так само, як і в попередньому випадку, кількість повторень циклу заздалегідь невідома.
Цикл з накопиченням характерний тим, що при черговому виконанні циклу нове значення вихідної змінної залежить від значення цієї ж змінної, визначеної на попередньому витку циклу. Накопичуватися може або сума значень, або добуток.
Цикл за лічильником. Знайти значення виразу:

де задані значення аргументів х ={2; 7; -1; 3; 17; 22; 5; 8} та коефіцієнтів а=3 і с=2.
Етапи розв'язання задачі:
У даному випадку задані вісім значень аргументу, і процес визначення Y аналогічний для кожного з них, тобто треба вісім разів повторити введення чергового (першого, другого, третього, ..., восьмого) аргументу х, обчислення і виведення функції Y.
Таким чином, початкове значення лічильника циклу має бути одиницею, кінцеве значення лічильника має дорівнювати восьми, після виконання циклу лічильник збільшує своє значення на одиницю, і цикл має виконуватися, доки значення лічильника не перевищить вісім.
Блок-схема алгоритму:

Блок № 3 — задає початкове значення лічильника циклу,
Блок № 4 — уводить чергове значення аргументу,
Блок № 5 — обчислює чергове значення функції для уведеного аргументу,
Блок № 6 — виводить обчислене значення функції,
Блок № 7 — збільшує значення лічильника циклу. Знак := використовується для того, щоб показати: обчислене значення виразу п +1 присвоюється як нове значення для п (лічильника циклу),
Блок № 8 — перевіряє нове значення лічильника (умову на продовження циклу). У зв'язку з тим, що умова перевіряється у кінці циклу — це цикл з післяумовою.
Блоки № 4—8 називаються тілом циклу. Якщо умова перевірки набуває результату ИСТИНА, тіло циклу виконується ще раз, а якщо умова набуває результату ЛОЖЬ, цикл припиняється.
Таким чином, у даному прикладі тіло циклу буде повторене 8 разів, доки значення лічильника не стане більшим за вісім.
Цикл за вхідним значенням. Обчислити значення виразу:

для заданих значень коефіцієнтів а і Ь та аргумента х, що змінюється від -4 до 6 з кроком 2.
Етапи розв'язання задачі:
1. Уводяться коефіцієнти а і Ь.
2. Уводиться початкове значення аргумента х (-4).
3. Обчислюється значення функції Y для поточного аргументу.
4. Виводиться отримане значення функції.
5. Значення аргументу х збільшується на 2.
6. Перевіряється умова продовження циклу: якщо нове значення аргументу не перевищує заданого кінцевого значення (6), цикл (блоки 3—6) виконується ще раз, у противному випадку робота завершується.
Цей цикл також є циклом з післяумовою, тому що перевірка умови проводиться у кінці циклу.
Блок-схема алгоритму.

Цикл за вихідним значенням (ітераційний цикл). Обчислити значення виразу:

Де n= 1, 2, 3, ...
Визначити таке n, при якому Y< ε, що задає точність обчислення.
Етапи розв'язання задачі:
1. Задається початкове значення п (1).
2. Обчислюється функція Y.
3. Проводиться перевірка, чи отримане значення функції дорівнює або менше за ε.
4. Якщо результат перевірки умови ИСТИНА, виводиться поточне значення п, отримане значення функції і цикл припиняється.
5. Якщо результат перевірки умови ЛОЖЬ, значення п збільшується на одиницю (п + 1), і цикл повторюється з блоку № 3.
Нижче подана блок-схема алгоритму розв'язання задачі.

Цикл, що використовується у прикладі, є циклом з передумовою, тому що блок перевірки розташований на початку циклу.
Цикл з накопиченням. Серед заданих десяти значень х = {2, 8, 0, -6, -4, 22, 5, -9, 13, —12} обчислити суму додатних чисел.
Даний цикл організовується як цикл по лічильнику. Якості змінна — накопичувач суми вибирається змінна S. Перед першим виконанням циклу початкове значення S вибирається рівним нулю (це проводиться з тієї причини, що при додаванні нуля до будь-якого значення результат не зміниться).
Етапи розв'язання задачі:
1. Задається початкове значення накопичувача суми S (0).
2. Задається початкове значення лічильника п (1).
3. Уводиться поточне значення х.
4. Проводиться перевірка, чи введене значення х є додатнім.
5. Якщо результатом перевірки умови є ИСТИНА, то провадиться накопичення суми (S + х), і значення лічильника збільшується на одиницю (п + 1).
6. Якщо результат перевірки умови — ЛОЖЬ, то накопичення суми не приводиться (пропускається), і значення лічильника збільшується на одиницю (п + 1).
7. Проводиться перевірка стану лічильника циклу. Якщо значення лічильника перевищує кількість заданих значень х (10), цикл припиняється, і виводиться отримане значення суми.
8. Якщо значення лічильника дорівнює або менше за кількість заданих х (10), цикл повторюється з блоку № 4.
Нижче подана блок-схема алгоритму розв'язання задачі.

У наведеному прикладі використовується цикл з післяумовою (перевірка умови виконання циклу — в кінці).
Аналогічно можна побудувати алгоритм для накопичення добутку, лише як початкове значення добутку треба використати одиницю, виходячи з того, що при множенні будь-якого числа на одиницю результат не зміниться.
Складні алгоритми. Складні алгоритми можуть містити сукупності перелічених вище циклів. Наприклад, визначити суму чисел натурального ряду доти, доки остаточне значення суми не перевищить 1000.
Вивести значення отриманої суми і кількість ітерацій (повторень циклу).
Основний цикл буде складатися з трьох типів: цикл з накопиченням (накопичується значення суми), цикл по вхідному значенню (перше значення натурального ряду є одиницею, а кожне наступне значення більше від попереднього на один) і цикл по вихідному значенню (ітераційний цикл продовжується, доки отримане значення суми не перевищить 1000). Переважаючим є тип циклу по вихідному значенню тому, що саме за вихідним значенням цикл або продовжується, або ні.
Етапи розв'язання задачі:
1. Задається початкове значення накопичувача суми S (0).
2. Задається початкове значення числа натурального ряду n (1).
3. Проводиться накопичення суми (S + п).
4. Проводиться перевірка значення накопиченої суми.
5. Якщо отримане значення суми менше або дорівнює 1000, збільшується значення числа натурального ряду (п + 1) і цикл повторюється з блоку № 3.
6. Якщо отримане значення суми більше за 1000, цикл припиняється.
7. Виводиться значення суми S.
8. Виводиться кількість повторень (n).
Нижче показана блок-схема алгоритму розв'язання задачі.

Таким чином, перш ніж починати розв'язання будь-яку задачу, треба:
• задачу формалізувати,
• розбити на кроки,
• кожному кроку дати відповідно розроблений модуль (або розробити його),
• скласти повний алгоритм,
• перевірити його функціональність,
• приступати до виконання.
Для цього зовсім не обов'язково подавати алгоритм схематично або описувати словесно, якщо він досить простий, але у разі розв'язання складних задач це є обов’язковою умовою успішного результату.
1.2. Системне забезпечення інформаційних процесів
Дата добавления: 2014-12-03; просмотров: 560; Мы поможем в написании вашей работы!; Нарушение авторских прав |