Матица достижимости неориентированного графа.

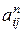Утверждение. Если А – матрица смежности графа , то элемент матрицы А^п равен числу маршрутов длины п, соединяющих вершины v_i и v_j графа G.

Доказательство. Методом математической индукции по числу п.

База индукции. При п = 1 утверждение верно, так как всякое ребро графа G – это маршрут длины 1.

Индуктивное предположение. Пусть утверждение справедливо для всех n £ k.

Индуктивный переход. Рассмотрим матрицу А^k+1. В ней .

В силу индуктивного предположения произведение есть число маршрутов длины k + 1, соединяющих вершину v_i с вершиной v_j с предпоследней вершиной всех таких маршрутов - v_m. Значит, сумма действительно равна числу маршрутов длин k + 1, соединяющих вершину v_i с вершиной v_j.

Следствие. Пусть – связный граф с р вершинами. Тогда любые две вершины графа можно соединить простой цепью. Но в простой цепи не может быть более (р - 1) ребер. Следовательно, все элементы матрицы отличны от нуля. Ясно, что верно и обратное утверждение.

В некоторых случаях при вычислениях степеней матрицы А и матрицы С важно знать не число соответствующих маршрутов, а только есть ли в графе эти маршруты или нет. Тогда при вычислении элементов матриц А², А³, … , А^р-1 вместо обычного сложения используют операцию Å, введенную нами при рассмотрении матриц конечных бинарных отношений. В результате матрицы А, А², А³, …,A^p-1, C состоят только из нулей и единиц.

Полученная таким образом матрица С называется матрицей достижимости графа G. Граф G связен тогда и только тогда, когда каждый элемент матрицы достижимости равен 1 (р ³ 3).