Напряженность электростатического поля. Принцип суперпозиции электрических полей. Теорема Гаусса.

Всякий заряд изменяет свойства окружающего пространства - создает в нем электрическое поле.

Электрическое поле - одна из форм существования материи, окружающей электрические заряды. Это поле проявляет себя в том, что помещенный в какую-либо его точку электрический заряд оказывается под действием силы.

Представление об электрическом поле было введено в науку в 30-х годах XIX столетия английским учеными Майклом Фарадеем.

Согласно Фарадею, каждый электрический заряд окружен созданным им электрическим полем, поэтому такой заряд иногда называют зарядом-источником. Заряд, с помощью которого исследуют поле заряда источника, называют пробным зарядом.

Для того чтобы сила, действующая на пробный заряд, характеризовала поле в данной точке, пробный заряд должен быть точечным.

Точечным зарядом называют заряженное тело, размерами которого можно пренебречь в условиях данной задачи, т.е. размеры которого малы по сравнению с расстояниями до других тел, с которыми он взаимодействует. При этом собственное электрическое поле пробного заряда должно быть столь мало, чтобы оно не изменяло поле заряда - источника. Чем меньше размер заряженного тела и чем слабее его собственное поле по сравнению с полем заряда-источника, тем точнее данное заряженное тело удовлетворяет условию пробного заряда.

Электрическое поле распространяется в вакууме со скоростью с= 3·1⁸ .

Поле неподвижных электрических зарядов - электростатическое.

Исследуем с помощью пробного заряда поле, создаваемое неподвижным зарядом - источником .

Сила, действующая на пробный заряд в данной точке поля, зависит от величины пробного заряда. Если брать различные пробные заряды, то и сила, действующая на них в данной точке поля, будет различной.

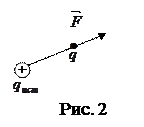Однако отношение силы к величине пробного заряда остается постоянным и характеризует уже само поле. Это отношение называется напряженностью электрического поля в данной точке.

, .

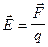Напряженность электрического поля - это векторная величина, численно равная силе, с которой поле действует на единичный положительный пробный заряд в данной точке поля и сонаправленная с этой силой (рис. 2).

Напряженность является основной характеристикой поля и полностью характеризует поле в каждой его точке по величине и направлению.

Напряженность поля точечного заряда.

Согласно закону Кулона

,

поэтому = .

Следовательно, напряженность электрического поля точечного заряда на расстоянии от этого заряда выражается формулой:

.

Электрическое поле удобно графически изображать с помощью картины так называемых силовых линий или линий напряженности.

Линией напряженности называется линия, касательная к которой в каждой точке совпадает по направлению с вектором напряженности в этой точке.

Линии напряженности поля, создаваемого неподвижными зарядами (рис. 3 а,б), всегда начинаются и кончаются на зарядах (или в бесконечности) и никогда не бывают замкнутыми. Более сильное поле изображается более плотно расположенными линиями напряженности. Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности площадки, перпендикулярной к линиям, было равно численному значению вектора . Линии напряженности никогда не пересекаются, т.к. их пересечение означало бы два различных направления вектора напряженности поля в одной и той же точке, что не имеет смысла.

Однородным называется поле, в котором напряженность во всех точках имеет одну и ту же величину и одинаковое направление, . В таком поле силовые линии параллельны и плотность их всюду одинакова, т.е. они расположены на одинаковом расстоянии друг от друга (рис. 3в).

Принцип суперпозиции.

Если электрическое поле в данной точке создано несколькими зарядами, то напряженность результирующего поля равна векторной сумме напряженностей полей, созданных каждым зарядом в отдельности (рис. 4).

,

.

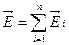Принцип суперпозиции является опытным фактом, справедливым вплоть до очень сильных полей. Поэтому же закону складываются не только статические, но и быстро меняющиеся электромагнитные поля

Потоком вектора напряженности через элементарную поверхность dS называется скалярное произведение

,

где - вектор, модуль которого равен , а направление совпадает с направлением нормали к площадке;

a- угол между векторами и ;

Е_п - проекция на направление нормали .

Просуммировав потоки через все элементарные площадки, на которые разбили поверхность S, получим поток вектора через поверхность S.

Потоком вектора через поверхность S называется интеграл

.

Для замкнутой поверхности .

Теорема Гаусса для электростатического поля в вакууме:

Поток вектора напряженности электростатического поля в вакууме через любую замкнутую поверхность прямо пропорционален алгебраической сумме зарядов, охватываемых этой поверхностью.

С помощью теоремы Гаусса были получены формулы, определяющие напряженность в ряде частных случаев.

Поле бесконечной равномерно заряженной плоскости (рис. 5):

.

Поверхностная плотность заряда - физическая величина, равная заряду, приходящемуся на единицу площади равномерно заряженной поверхности.

Если поверхность заряжена неравномерно,

.

Поле 2-х бесконечных разноименно заряженных плоскостей (рис. 6):

Полученный результат справедлив для плоскостей конечных размеров, расстояние между которыми мало по сравнению с их размерами (конденсатор).

Помимо основного вектора в теории электричества оказывается необходимо ввести еще вектор электрической индукции (или вектор смещения).

, =1 .