
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сложение сходящихся сил. Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.
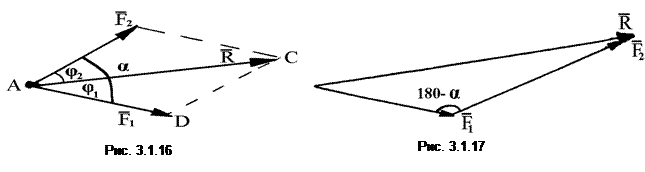
Сложить две или несколько сил – значит заменить эти силы одной силой, им эквивалентной, т.е. найти их равнодействующую (рис. 3.1.16).
Из ∆ADC:  т.к. cos(180 – a) = –cosa, то получим
т.к. cos(180 – a) = –cosa, то получим
 , (3.1.2)
, (3.1.2)
 . (3.1.3)
. (3.1.3)
Найти равнодействующую можно также, построив половину параллелограмма – треугольник сил, в котором равнодействующая является замыкающей стороной (рис. 3.1.17).
Равнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, равна по модулю и направлению диагонали параллелепипеда, построенного на этих трех силах (рис. 3.1.18).
Так как 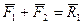 , а
, а  , то
, то  .
.
Равнодействующая нескольких сходящихся сил выражается по модулю и направлению вектором, соединяющим начальную и конечную точки ломаной линии (правило силового многоугольника) (рис. 3.1.19).
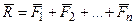 или
или  . (3.1.4)
. (3.1.4)
Сходящиеся силы уравновешиваются в случае, если их равнодействующая равна нулю, т.е. многоугольник сил замкнут. Конец вектора последней силы совпадает с началом вектора первой силы, все силы направлены по контуру многоугольника в одну сторону, т.е.  .
.
Согласно, аналитическому условию равновесия при R = 0 получим
 ,
,
где ∑ Fix, ∑ Fiy, ∑ Fiz – проекции сил на координатные оси. Следовательно,
∑ Fix = 0; ∑ Fiy = 0; ∑ Fiz = 0. (3.1.5)
Для равновесия тела при действии на него пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций этих сил на каждую из координатных осей была равна нулю.
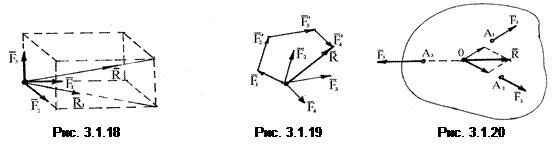
Теорема о равновесии трех непараллельных сил.Линии действия трех непараллельных взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке. К твердому телу в точках А1, А2, А3 приложены три непараллельные взаимно уравновешивающиеся силы  лежащие в одной плоскости. Перенесем силы
лежащие в одной плоскости. Перенесем силы 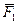 и
и  в точку О и найдем их равнодействующую. Сила
в точку О и найдем их равнодействующую. Сила 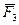 будучи уравновешивающей системы сил
будучи уравновешивающей системы сил 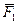 и
и  , равна по модулю их равнодействующей
, равна по модулю их равнодействующей  и направлена по линии ее действия в противоположную сторону (рис. 3.1.20).
и направлена по линии ее действия в противоположную сторону (рис. 3.1.20).
 |
Сходящиеся силы, приложенные к ВС. Часто для качественной оценки сил, действующих на ВС, их представляют в виде сходящихся сил. Равнодействующую
 сил давления воздушного потока на крыло и сил трения протекающего воздуха о его поверхность можно считать суммой двух сходящихся сил (рис. 3.1.21):
сил давления воздушного потока на крыло и сил трения протекающего воздуха о его поверхность можно считать суммой двух сходящихся сил (рис. 3.1.21):
 ,
,
где  – аэродинамическая сила крыла;
– аэродинамическая сила крыла;
 – сила лобового сопротивления;
– сила лобового сопротивления;
 – аэродинамическая подъемная сила крыла.
– аэродинамическая подъемная сила крыла.
В виде сходящихся сил представляют часто и силы, действующие на ВС в полете. При наборе высоты, например, в упрощенную систему действующих на ВС сходящихся сил входят (рис. 3.1.22):
 – сила тяжести (вес самолета);
– сила тяжести (вес самолета);
 – тяга винта (или газотурбинного двигателя);
– тяга винта (или газотурбинного двигателя);
 – сила лобового сопротивления самолета;
– сила лобового сопротивления самолета;
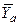 – аэродинамическая подъемная сила.
– аэродинамическая подъемная сила.
Аналогичным образом упрощают систему сил, действующих на ВС и в других режимах полета.

 |
Пример. Ось колеса шасси легкого самолета крепится к фюзеляжу с помощью трех шарнирно закрепленных подкосов (рис. 3.1.23), оси которых пересекаются в точке О. Ось подкоса 1 совпадает с осью колеса, подкос 2 расположен в горизонтальной плоскости под углом a = 30° к оси первого подкоса, а подкос 3 – в вертикальной плоскости под углом b = 60°. На колесо действуют силы Р = 10 кН и F = 3 кН. Определите усилия в подкосах.
Решение. Рассмотрим равновесие колеса. На колесо действуют две активные силы (  и
и 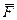 ) и наложены связи – невесомые стержни 1, 2, 3. Используя аксиому освобождаемости от связей, мысленно отбрасываем связи, заменяя их действие реакциями
) и наложены связи – невесомые стержни 1, 2, 3. Используя аксиому освобождаемости от связей, мысленно отбрасываем связи, заменяя их действие реакциями  . Выбираем оси координат так, чтобы решение задачи было наиболее простым. Составляем условия равновесия колеса, находящегося под действием пространственной системы сходящихся сил
. Выбираем оси координат так, чтобы решение задачи было наиболее простым. Составляем условия равновесия колеса, находящегося под действием пространственной системы сходящихся сил  :
:
∑ Fix =0; – F – S2 sin a = 0; S2 = – 6 кН.
∑ Fiy =0; P + S3 sin b = 0; S3 = – 11,5 кН.
∑ Fiz =0; S1 + S2 cos a + S3 cos b = 0; S1 = 11 кН.
Освобождая тело от связей, мы полагали все стержни растянутыми. Знак «минус» в полученных значениях реакций S2 и S3 означает, что в действительности они сжаты.
Тема 3. Теория пар сил
Момент силы относительно центра. Опыт показывает, что эффект действия силы, приложенной к телу (например, к рычагу, штурвалу), на разных расстояниях от точки закрепления тела, зависит от так называемого момента силы относительно точки закрепления.
Моментом силы 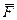 относительно центра О называется произведение модуля силы на кратчайшее расстояние от центра О до линии действия силы:
относительно центра О называется произведение модуля силы на кратчайшее расстояние от центра О до линии действия силы:
M0( 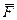 ) = ± Fh, (3.1.6)
) = ± Fh, (3.1.6)
где h – кратчайшее расстояние от центра О до линии действия силы 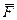 .
.
Момент силы считается положительным, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки и отрицательным, если по ходу часовой стрелки (рис. 3.1.24, 3.1.25). Момент силы измеряется в Н·м.

Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия. Момент силы относительно центра О равен нулю, если сила равна нулю или, если линия действия силы проходит через центр О (плечо равно нулю).
Графически абсолютная величина момента силы относительно центра О выражается удвоенной площадью ΔОАВ:
M0 ( 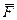 ) = 2S ∆ОАВ. (3.1.7)
) = 2S ∆ОАВ. (3.1.7)
 Момент силы относительно центра как векторное произведение. Введенного понятия «момент силы относительно центра как алгебраическая величина» оказывается недостаточно в случае сил, произвольно расположенных в пространстве. Плоскости поворота у разных сил будут различными и должны задаваться дополнительно. Удобно ввести понятие «момент силы относительно центра как вектор», модуль которого равен произведению модуля силы на ее плечо, а направление перпендикулярно плоскости, проходящей через линию действия силы и центр момента.
Момент силы относительно центра как векторное произведение. Введенного понятия «момент силы относительно центра как алгебраическая величина» оказывается недостаточно в случае сил, произвольно расположенных в пространстве. Плоскости поворота у разных сил будут различными и должны задаваться дополнительно. Удобно ввести понятие «момент силы относительно центра как вектор», модуль которого равен произведению модуля силы на ее плечо, а направление перпендикулярно плоскости, проходящей через линию действия силы и центр момента.
Вектор момента силы  прикладывают в центре момента и направляют в сторону, откуда сила видна вращающей тело в направлении, противоположном ходу часовой стрелки (рис. 3.1.26). Соединим центр момента О с точкой приложения силы радиусом-вектором
прикладывают в центре момента и направляют в сторону, откуда сила видна вращающей тело в направлении, противоположном ходу часовой стрелки (рис. 3.1.26). Соединим центр момента О с точкой приложения силы радиусом-вектором 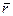 и найдем векторное произведение
и найдем векторное произведение  .
.
По определению векторного произведения
|  |= 2S×∆ОАВ.
|= 2S×∆ОАВ.
Модуль вектора момента силы  также равен удвоенной площади ∆ОАВ.
также равен удвоенной площади ∆ОАВ.
Тогда
 =
=  .
.
Направление векторного произведения также совпадает с направлением вектора момента. Следовательно, вектор-момент  силы
силы 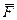 относительно центра О можно рассматривать как векторное произведение радиус-вектора
относительно центра О можно рассматривать как векторное произведение радиус-вектора 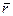 , проведенного из этой точки в точку приложения силы, на вектор силы
, проведенного из этой точки в точку приложения силы, на вектор силы 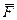 :
:
 (3.1.8)
(3.1.8)
Момент силы относительно оси. Чтобы охарактеризовать вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг некоторой оси, вводится понятие «момента силы относительно оси».
 Рассмотрим твердое тело, которое может вращаться вокруг оси OZ (рис.3.1.27). Пусть на тело действует сила
Рассмотрим твердое тело, которое может вращаться вокруг оси OZ (рис.3.1.27). Пусть на тело действует сила 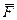 , приложенная в точке А. Проведем через точку А плоскость OXY, перпендикулярную оси OZ, и разложим силу
, приложенная в точке А. Проведем через точку А плоскость OXY, перпендикулярную оси OZ, и разложим силу 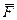 на две составляющие:
на две составляющие:  , параллельную оси OZ, и
, параллельную оси OZ, и  , лежащую в плоскости XY. Составляющая, параллельная оси OZ, крутящего момента не создает, а, следовательно, весь вращательный эффект, создаваемый силой
, лежащую в плоскости XY. Составляющая, параллельная оси OZ, крутящего момента не создает, а, следовательно, весь вращательный эффект, создаваемый силой 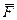 ,будет вызван ее составляющей
,будет вызван ее составляющей  .
.
Mz ( 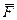 ) = M0 (
) = M0 (  ) = ± Fxy h = ± 2S ∆OAB1. (3.1.9)
) = ± Fxy h = ± 2S ∆OAB1. (3.1.9)
Моментом силы относительно оси называют момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Момент силы относительно оси считается положительным, если смотря навстречу оси Z, можно видеть проекцию Fxy, стремящейся вращать плоскость XY вокруг оси Z в сторону, противоположную вращению часовой стрелки.
Момент силы относительно оси равен нулю:
1) если Fxy = 0, т.е. линия действия силы параллельна оси OZ;
2) если h = 0, т.е. линия действия силы пересекает ось OZ.
Следовательно, если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю.
 Пара сил. Момент пары. Система двух равных по модулю, параллельных и противоположно направленных сил
Пара сил. Момент пары. Система двух равных по модулю, параллельных и противоположно направленных сил  называется парой сил (рис. 3.1.28).
называется парой сил (рис. 3.1.28).
Пара сил не имеет равнодействующей, и силы пары не уравновешиваются. Действие пары на тело характеризуется ее моментом:
1) вектор-момент перпендикулярен плоскости действия пары;
2) направлен в ту сторону, чтобы, смотря с его конца, вращение было происходящим против хода часовой стрелки;
3) величина вектора 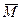 равна в выбранном масштабе численному значению момента пары.
равна в выбранном масштабе численному значению момента пары.
Вектор-момент пары равен векторному произведению радиуса-вектора 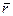 на ту из сил пары, к началу которой направлен вектор
на ту из сил пары, к началу которой направлен вектор  :
:
 , (3.1.10)
, (3.1.10)
или
 , (3.1.11)
, (3.1.11)
по модулю
M = r Fsin α = Fh; M = ± Fh. (3.1.12)
Пары сил в пространстве эквивалентны, если их моменты геометрически равны. Геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары:

 . (3.1.13)
. (3.1.13)
Пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю. Если пары сил расположены в одной плоскости, то моменты этих пар сил, направленные по одной прямой, складываются алгебраически.
 Момент пары сил, эквивалентный системе пар сил на плоскости, равен алгебраической сумме моментов составляющих пар (рис. 3.1.29):
Момент пары сил, эквивалентный системе пар сил на плоскости, равен алгебраической сумме моментов составляющих пар (рис. 3.1.29):
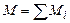 , (3.1.14)
, (3.1.14)
где Mi = ± Fi di .
Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю:
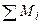 = 0.
= 0.
 Силовое воздействие на ВС часто приводится к паре сил. Например, аэродинамические силы (силы сопротивления воздуха вращению) воздушного винта складываются в пару, называемую аэродинамическим (реактивным) моментом винта Мв (рис. 3.1.30). Чем большую мощность развивает двигатель, тем больше реактивный момент, вызывающий крен ВС. Этот момент уравновешивают некоторым отклонением элеронов; аэродинамические силы
Силовое воздействие на ВС часто приводится к паре сил. Например, аэродинамические силы (силы сопротивления воздуха вращению) воздушного винта складываются в пару, называемую аэродинамическим (реактивным) моментом винта Мв (рис. 3.1.30). Чем большую мощность развивает двигатель, тем больше реактивный момент, вызывающий крен ВС. Этот момент уравновешивают некоторым отклонением элеронов; аэродинамические силы 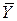 Э.пр и
Э.пр и 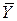 Э..лев составляют пару с моментом, равным значению реактивного момента воздушного винта и обратным его направлению.
Э..лев составляют пару с моментом, равным значению реактивного момента воздушного винта и обратным его направлению.
Тема 4. Система произвольно расположенных сил
Теорема о параллельном переносе силы (теорема Пуансо). Действие силы на АТТ не изменится, если перенести ее параллельно самой себе в некоторую точку (центр приведения) присоединив при этом пару сил. Момент присоединенной пары равен моменту приведенной силы, относительно центра приведения. В точке А (рис. 3.1.31) приложена сила 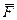 , которую необходимо перенести в точку В. Как это сделать? В точке В прикладываем силы, равные по модулю сил
, которую необходимо перенести в точку В. Как это сделать? В точке В прикладываем силы, равные по модулю сил  ; (
; (  ) ≡ (
) ≡ ( 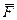 ); (
); ( 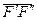 ) ≡ 0. Получили эквивалентную
) ≡ 0. Получили эквивалентную 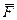 систему трех сил, которую можно рассматривать как совокупность силы
систему трех сил, которую можно рассматривать как совокупность силы  и пары сил
и пары сил  с моментом
с моментом  (рис. 3.1.32).
(рис. 3.1.32).

Пару  называют присоединенной; ее момент равен моменту переносимой силы относительно центра приведения и, следовательно, зависит от положения этого центра.
называют присоединенной; ее момент равен моменту переносимой силы относительно центра приведения и, следовательно, зависит от положения этого центра.
 Приведение произвольной пространственной системы сил к данному центру. Главный вектор и главный момент.Систему сил, приложенных к телу, можно упростить, используя теорему о параллельном переносе силы. В результате приведения произвольной пространственной системы сил к данному центру в общем случае получаем главный вектор, равный геометрической сумме всех сил системы, и главный момент, равный геометрической сумме моментов всех приводимых сил относительно центра приведения (рис. 3.1.33).
Приведение произвольной пространственной системы сил к данному центру. Главный вектор и главный момент.Систему сил, приложенных к телу, можно упростить, используя теорему о параллельном переносе силы. В результате приведения произвольной пространственной системы сил к данному центру в общем случае получаем главный вектор, равный геометрической сумме всех сил системы, и главный момент, равный геометрической сумме моментов всех приводимых сил относительно центра приведения (рис. 3.1.33).
Сложим  и т.д., получим силовой многоугольник, где
и т.д., получим силовой многоугольник, где
 . (3.1.15)
. (3.1.15)
Затем векторно сложим векторы моментов:
 (3.1.16)
(3.1.16)
 , (3.1.17)
, (3.1.17)
где  (x1, y1, z1),
(x1, y1, z1),  (x2, y2, z2) проекции на координатные оси каждой из сил.
(x2, y2, z2) проекции на координатные оси каждой из сил.
Главный вектор инвариантен по отношению к центру приведения. Главный момент зависит от выбора центра приведения.
По модулю главный вектор вычисляется следующим образом:
R* =  , (3.1.18)
, (3.1.18)
где
Rx = X1 + X2 +...+ Xn = ∑ Xi; (3.1.19).
Ry = Y1 + Y2 +...+ Yn = ∑ Yi;
Rz = Z1 + Z2 +...+ Z n = = ∑ Z –
проекции главного вектора на координатные оси  * (Rx, Ry, Rz).
* (Rx, Ry, Rz).
Направление находим по направляющим косинусам:
cos(  *,
*,  ) =
) =  ; cos(
; cos(  *,
*,  ) =
) =  ; cos(
; cos(  *,
*, 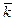 ) =
) =  . (3.1.20)
. (3.1.20)
Главный момент
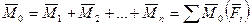 ;
;
M0x = ∑Mx ( 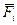 ); M0y =∑My(
); M0y =∑My( 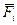 ); M0z = ∑ Mz(
); M0z = ∑ Mz( 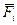 ); (3.1.21)
); (3.1.21)
M0 =  . (3.1.22)
. (3.1.22)
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех этих сил на каждую из координатных осей равнялась нулю и чтобы алгебраическая сумма моментов всех сил системы относительно каждой из трех координатных осей равнялась нулю:
∑ Xi = 0; ∑Yi = 0; ∑Zi = 0;
∑ Mx ( 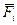 ) = 0; ∑My (
) = 0; ∑My ( 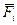 ) = 0; ∑Mz (
) = 0; ∑Mz ( 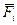 ) = 0. (3.1.23)
) = 0. (3.1.23)
Система параллельных сил. Если ось OZ параллельна силам, то три уравнения (3.1.23) обращаются в тождества, так как проекции сил на оси OX и OY и их моменты относительно оси OZ равны нулю. Оставшиеся три уравнения являются уравнениями равновесия параллельных сил в пространстве (рис. 3.1.34):
Zi = 0; ∑ Mx ( 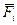 ) = 0; ∑My (
) = 0; ∑My ( 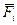 ) = 0. (3.1.24)
) = 0. (3.1.24)
Для параллельных сил, расположенных в плоскости XOY (рис. 3.1.35), имеем два уравнения равновесия:
∑Yi = 0; ∑M0 ( 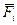 ) = 0. (3.1.25)
) = 0. (3.1.25)
Плоская система произвольно расположенных сил. Если силы действуют в плоскости XOY (рис.3.1.36), то суммы проекций их на ось OZ и моментов относительно осей OX и OY равны нулю.

При равновесии тела под действием плоской системы сил суммы их проекций на оси координат и сумма моментов относительно произвольного центра, лежащего в плоскости сил, равны нулю:
∑ Xi = 0; ∑Yi = 0; ∑M0 ( 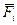 ) = 0. (3.1.26)
) = 0. (3.1.26)
Примеры упрощения системы сил, действующих на ВС. Силы взаимодействия ВС с поверхностью взлетно-посадочной полосы (ВПП) и воздухом при движении по земле и в полете подчиняются сложным закономерностям. Во всех случаях систему сил, действующих на ВС, упрощают. Например, воздушное давление, неравномерно распределенное по нижней и верхней поверхностям крыла (или стабилизатора, киля), часто суммируют и относят к одной поверхности.
Силы, действующие на ВС в горизонтальном полете с постоянной скоростью без бокового ветра, могут быть приведены к плоской системе сил (рис. 3.1.37).
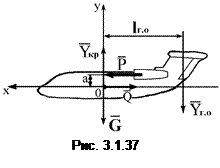 Вес ВС (
Вес ВС (  ), подъемная сила крыла (
), подъемная сила крыла (  ) и горизонтального оперения (
) и горизонтального оперения (  ), тяга двигателей (
), тяга двигателей (  ) и сила лобового сопротивления (
) и сила лобового сопротивления ( 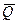 )удовлетворяют трем уравнениям равновесия:
)удовлетворяют трем уравнениям равновесия:
1. Условие сохранения постоянной скорости:
∑ Xi = 0, P – Q = 0; (3.1.27)
2. Условие сохранения постоянной высоты:
Yi = 0, Yкр – G – Yг.о = 0. (3.1.28)
3. Условие сохранения горизонтального положения ВС:
∑M0 ( 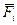 ) = 0, Pa – Yг.о·lг.о = 0. (3.1.29)
) = 0, Pa – Yг.о·lг.о = 0. (3.1.29)
Теорема о моменте равнодействующей (теорема Вариньона). Момент равнодействующей произвольной системы сил относительно любой точки (оси) равен сумме моментов составляющих сил относительно той же точки (оси) (рис. 3.1.38).
 Пусть действующая на тело произвольная система сил приводится к равнодействующей
Пусть действующая на тело произвольная система сил приводится к равнодействующей 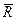 . Уравновесим тело, приложив к нему силу
. Уравновесим тело, приложив к нему силу  = –
= – 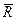 . Новая система сил находится в равновесии, и для нее справедливо уравнение равновесия:
. Новая система сил находится в равновесии, и для нее справедливо уравнение равновесия:
∑Mc( 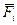 ) + Mc(
) + Mc(  ) = 0,
) = 0,
но
Mc (  ) = – Mc(
) = – Mc(  ),∑Mc (
),∑Mc ( 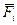 ) – Mc (
) – Mc (  ) = 0,
) = 0,
или
Mc(  ) = ∑Mc (
) = ∑Mc ( 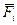 ). (3.1.30)
). (3.1.30)
 Понятие о моменте устойчивости и моменте опрокидывания. При опробовании двигателя главные колеса шасси уперты в подкладки D, а хвостовое колесо не отрывается от земли. Будем считать, что на ВС действует только две силы:
Понятие о моменте устойчивости и моменте опрокидывания. При опробовании двигателя главные колеса шасси уперты в подкладки D, а хвостовое колесо не отрывается от земли. Будем считать, что на ВС действует только две силы:  – тяга винта и
– тяга винта и  – вес ВС, лежащие в вертикальной плоскости (рис. 3.1.39).
– вес ВС, лежащие в вертикальной плоскости (рис. 3.1.39).
Выясним условия, при которых хвост прижат к земле. Для этого найдем равнодействующую  сил
сил  и
и  . Возможны два случая:
. Возможны два случая:
1. Равнодействующая  проходит слева от точки D.
проходит слева от точки D.
2. Равнодействующая  проходит справа от точки D.
проходит справа от точки D.
В первом случае ВС находится в равновесии, опрокидывание невозможно. Равнодействующая  стремится повернуть ВС вокруг точки D против часовой стрелки:
стремится повернуть ВС вокруг точки D против часовой стрелки:
MD(  ) > 0: MD(
) > 0: MD(  ) = MD (
) = MD (  ) + MD (
) + MD (  ),
),
то
MD(  ) + MD(
) + MD(  ) > 0,
) > 0,
тогда
MD(  ) > MD(
) > MD(  ) (3.1.31)
) (3.1.31)
или Ga > Pb– момент устойчивости больше момента опрокидывания.
Второй случай, если  лежит справа от точки D, то MD(
лежит справа от точки D, то MD(  ) < 0, а т.к.
) < 0, а т.к.
MD(  ) = Ga – Pb, (3.1.32)
) = Ga – Pb, (3.1.32)
то Ga – Pb < 0 или Ga < Pb, равновесие ВС нарушится, его хвост поднимется, возможно капотирование ВС. Отношение момента устойчивости к опрокидывающему моменту называется коэффициентом устойчивости.
Тема 5. Центр параллельных сил и центр тяжести
Центр параллельных сил. Центром параллельных сил называется точка, через которую проходит линия действия равнодействующей, не изменяющая своего положения при повороте всех сил в одну сторону и на один и тот же угол вокруг их точек приложения. Координаты точки С будут равны:
XС =  ; YС =
; YС =  ; ZС =
; ZС =  . (3.1.33)
. (3.1.33)
Центр тяжести.Согласно закону всемирного тяготения на все частицы тела вблизи земной поверхности действуют силы тяжести, сходящиеся в центре Земли. Размеры рассматриваемых тел невелики по сравнению с радиусом земного шара, а поэтому силы тяжести частиц тела можно считать параллельными.
Координаты центра тяжести тела (точки приложения силы тяжести  ):
):
XС =  ; YС =
; YС = 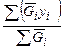 ; ZС =
; ZС =  . (3.1.34)
. (3.1.34)
Понятие центра тяжести тела теряет смысл для тел, находящихся за пределами земного тяготения. Наиболее общей характеристикой распределения вещества тела является центр масс. Зная, что G = mg, где g – ускорение свободного падения, найдем координаты центра масс тела:
XС =  ; YС =
; YС =  ; ZС =
; ZС =  . (3.1.35)
. (3.1.35)
Центр масс объема.Масса частицы тела mi = Viρ, тогда, подставляя в формулы (3.1.35), получим
XС =  ; YС =
; YС =  ; ZС =
; ZС =  . (3.1.36)
. (3.1.36)
Центр масс площади. Статические моменты. Положение ЦМ однородной пластины зависит только от формы пластины:
XС =  ; YС =
; YС =  ; ZC =
; ZC =  . (3.1.37)
. (3.1.37)
где Si – площадь частей фигуры;
xi, yi – их координаты;
∑Si – площадь всей фигуры.
Суммы произведений площадей отдельных частей фигуры на их расстояния до осей называются статическими моментами плоской фигуры:
 . (3.1.38)
. (3.1.38)
Статические моменты, измеряемые в сантиметрах или миллиметрах, могут быть положительными, отрицательными или равными нулю (если ось проходит через ЦМ плоской фигуры).
Положение центра масс простейших фигур.ЦМ параллелограмма находится в точке пересечения его диагоналей (рис. 3.1.40, а). ЦМ площади треугольника лежит в точке пересечения его медиан. Так как точка пересечения медиан треугольника отстоит от его основания на расстоянии одной трети длины медианы, то, следовательно, ЦМ площади треугольника отстоит от основания на расстоянии одной трети высоты (рис. 3.1.40, б, в). У треугольника (рис. 3.1.40, г), координаты вершин которого известны, ЦМ определяется по формулам:

 . (3.1.39)
. (3.1.39)

Рис. 3.1.40
Центр масс дуги радиуса R отстоит от центра дуги (рис. 3.1.41, а) на расстоянии
ОС =  ,
,
где R – радиус дуги, α – половина центрального угла, рад.
Для сектора ОС = 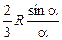 (рис. 3.1.41, б). В частном случае для полукруга (рис. 3.1.41, в)
(рис. 3.1.41, б). В частном случае для полукруга (рис. 3.1.41, в) 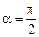 , тогда ОС =
, тогда ОС =  .
.

Рис. 3.1.41
Центровка самолета. Положение ЦМ ВС имеет исключительно важное значение для его устойчивости в полете. Нередко неправильная центровка является причиной серьезных летных происшествий.
Очень жесткие ограничения накладываются на положение ЦМ вдоль оси ОХ. Во-первых, ЦМ должен быть расположен впереди основных опор (рис. 3.1.42, а) для того, чтобы на земле предотвратить опрокидывание самолета на хвост. Во-вторых, ЦМ должен располагаться в определенном диапазоне расстояний впереди так называемого фокуса крыла – точки приложения приращения подъемной силы, вызванного изменением угла атаки (рис. 3.1.42, б). В этом случае самолет будет обладать продольной устойчивостью, т.е. свойством возвращаться без вмешательства экипажа к первоначальному режиму полета после прекращения действия случайных сил.
Действительно, если случайные силы (при полете в турбулентной атмосфере) создают возмущающий момент Мвозм (рис.3.1.42, в) в сторону увеличения угла атаки, то подъемная сила получит положительное приращение  . Момент силы Δ
. Момент силы Δ  относительно ЦМ, направленный в противоположную сторону (восстанавливающий момент) вернет крыло к первоначальному углу атаки.
относительно ЦМ, направленный в противоположную сторону (восстанавливающий момент) вернет крыло к первоначальному углу атаки.

Рис. 3.1.42
Смещение ЦМ за предельно заднее его положение (см. рис. 3.1.42, б) опасно уменьшает запас продольной устойчивости самолета, смещение ЦМ вперед за предельно переднее положение (см. рис. 3.1.42, а) затрудняет пилотирование самолета на малых скоростях при снижении перед посадкой.
Положение ЦМ самолетов характеризуется так называемой центровкой  , равной выраженному в процентах расстоянию ЦМ от носка средней аэродинамической хорды крыла (САХ) – bа:
, равной выраженному в процентах расстоянию ЦМ от носка средней аэродинамической хорды крыла (САХ) – bа:
 % ,
% ,
где хт – расстояние ЦМ от носка САХ;
ba – длина САХ.
Для каждого самолета задан интервал эксплуатационных центровок (для Як-40 17–31 %, Ту-134А 21–38% CАХ). Координаты ХС, YС ЦМ самолета в процессе проектирования определяют расчетным путем, а, зная эти величины и расстояние Xa до носка САХ, а также загрузку и количество топлива в баках, можно найти центровку самолета:
 100% .
100% .
Она меняется в течение одного полета в связи с расходованием топлива. Центровку определяют перед каждым рейсом самолета.
Тема 6. Понятие о трении. Виды трения
Трение – сопротивление, возникающее при движении одного шероховатого тела по поверхности другого. При скольжении тел возникает трение скольжения, при качении – трение качения. Природа сопротивлений движению в разных случаях различна. Трение является сложным физико-механическим явлением. Оно возникает вследствие шероховатости поверхности и действия молекулярного сцепления между частицами прижатых друг к другу тел. Трение зависит от материала трущихся тел, температуры, наличия между телами смазки, скорости скольжения других факторов, учет которых затруднен.
Трение скольжения. Рассмотрим простейший случай – трение между негладкой горизонтальной поверхностью и лежащим на ней тяжелым негладким телом. Причина трения – механическое зацепление микронеровностей соприкасающихся поверхностей. Сила сопротивления движению при скольжении называется силой трения скольжения (рис. 3.1.43, а).
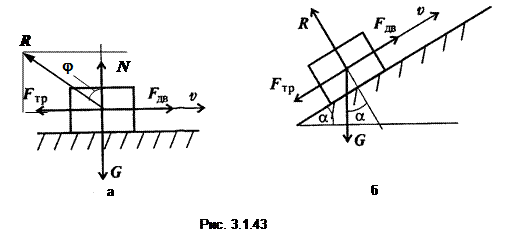
Законы трения скольжения:
1. Сила трения скольжения прямо пропорциональна силе нормального давления:
Fтр = Ff = fN,
где N – сила нормального давления, направлена перпендикулярно опорной поверхности;
f – коэффициент трения скольжения.
В случае движения тела по наклонной плоскости (рис. 3.1.43, б)
R = Gcos a,
где a – угол наклона плоскости к горизонту.
Сила трения всегда направлена в сторону, обратную направлению движения.
2. Сила трения меняется от нуля до некоторого максимального значения, называемого силой трения покоя (статическое трение):
0 < Ff < Ff 0,
где Ff 0 – статическая сила трения (сила трения покоя).
3. Сила трения при движении меньше силы трения покоя. Сила трения при движении называется динамической силой трения (Ff ):
Ff  Ff 0.
Ff 0.
Поскольку сила нормального давления, зависящая от веса и направления опорной поверхности, не меняется, то различают статический и динамический коэффициенты трения:
Ff = f R; Ff0 = f0 N.
Коэффициент трения скольжения зависит от следующих факторов:
 1. Материал. Материалы делятся на фрикционные (с большим коэффициентом трения) и антифрикционные (с малым коэффициентом трения), например, f = 0,1–0,15 (при скольжении стали по стали всухую), f = 0,2–0,3 (при скольжении стали по текстолиту).
1. Материал. Материалы делятся на фрикционные (с большим коэффициентом трения) и антифрикционные (с малым коэффициентом трения), например, f = 0,1–0,15 (при скольжении стали по стали всухую), f = 0,2–0,3 (при скольжении стали по текстолиту).
2. Наличие смазки. Например, f = 0,04–0,05 (при скольжении стали по стали со смазкой).
Угол j0 между направлениями нормальной реакции (N) и полной реакции (Rmax), соответствующей максимальному значению силы трения скольжения в покое (Fтр. max), называется углом трения.
Из рис. 3.1.44 видно, что
 .
.
Так как Fmax = f0 N, то отсюда находим следующую связь между углом трения (j0) и коэффициентом трения скольжения в покое (f0):
f0 = tgj0,
т.е. коэффициент трения скольжения в покое равен тангенсу угла трения.
Конус с вершиной в точке касания тел, образующая которого составляет угол трения с нормалью к поверхности трущихся тел, называется конусом трения (рис. 3.1.45).
Если коэффициент трения скольжения в покое при скольжении тела по поверхности, которая служит связью, в различных направлениях один и тот же, то полная реакция этой связи (Rmах) отклоняется от нормальной реакции (N) во всех направлениях на одинаковый угол трения j0, и конус трения будет круглым с углом при вершине, равным 2j0. Однако это условие не соблюдается, например, при скольжении по дереву в направлении волокон и в направлении, перпендикулярном к ним. Конус трения в этом случае будет сплющен в направлении волокон.

Рис. 3.1.45
До тех пор пока линия действия равнодействующей всех сил, приложенных к телу, каков бы ни был ее модуль, проходит внутри конуса трения, скольжение тела по связи не возникает (a £ j0). Этим объясняются известные явления заклинивания, или самоторможения частей машины, когда никакой приложенной внутри конуса трения силой не удастся сдвинуть с места соответствующую часть машины.
Трение качения.Сопротивление при качении связано с взаимной деформацией грунта и колеса и значительно меньше трения скольжения.
Обычно грунт считают мягче колеса, тогда в основном деформируется грунт, и в каждый момент колесо должно перекатываться через выступ грунта. Для равномерного качения колеса необходимо прикладывать силу Fдв (рис. 3.1.46).
 Условие качения колеса состоит в том, что движущий момент должен быть не меньше момента сопротивления:
Условие качения колеса состоит в том, что движущий момент должен быть не меньше момента сопротивления:
Fдв r ³ Nk: N = G;  ,
,
где k – максимальное значение плеча (половина колеи), принимается за коэффициент трения качения, см.
Ориентировочные значения k (определяются экспериментально): сталь по стали – k = 0,005 см, резиновая шина по шоссе – k = 0,24 см.
Контрольные вопросы
1. Какие основные понятия используются в статике?
2. Охарактеризуйте понятие сосредоточенной и распределенной сил.
3. Какие системы сил называются эквивалентными, какие – уравновешенными?
4. Какую силу называют равнодействующей?
5. Сформулируйте аксиомы статики.
6. Основные типы связей. Направление их реакций.
7. Какая система сил называется сходящейся? Как найти равнодействующую системы сходящихся сил.
8. Назовите аналитические условия равновесия системы сходящихся сил, расположенных на плоскости и в пространстве.
9. Теорема о равновесии трех непараллельных сил.
10. Чему равен момент силы относительно точки? Когда он равен нулю?
11. В каких случаях момент силы относительно оси равен нулю?
12. Что такое пара сил? Чему равен момент пары?
13. Как суммируются пары сил? Чем может быть заменена система пар сил, действующих на твердое тело?
14. Что такое пара сил трения качения? Почему она возникает? От чего зависит ее момент?
15. Теорема о параллельном переносе силы.
16. Приведение произвольной плоской системы сил к данному центру. Главный вектор и главный момент.
17. Аналитические условия равновесия различных систем сил.
18. Теорема о моменте равнодействующей произвольной пространственной системы сил относительно точки и оси (теорема Вариньона).
19. Дайте определение центра параллельных сил и центра тяжести твердого тела.
20. Запишите формулы, по которым вычисляются координаты центров тяжести простейших фигур.
21. Перечислите основные способы, используемые при определении положения центров тяжести твердых тел.
22. Как определяется положение центров тяжести симметричных тел?
Кинематика
Тема 7. Основные понятия кинематики.
Способы задания движения
Кинематика – раздел теоретической механики, в котором изучается механическое движение без учета масс и приложения сил. Всякое движение тел происходит в пространстве и во времени, по отношению к другим телам, с которыми жестко связывают систему координат, называемую системой отсчета. Абсолютно неподвижных тел в окружающем нас мире нет, поэтому движение и покой любого тела являются относительными. При изучении движения ВС по аэродрому или при полетах на небольшие расстояния Землю считают неподвижной и связывают с ней систему отсчета. При скоростных полетах на большие расстояния систему отсчета по-прежнему связывают с Землей, но не считают ее неподвижной, а учитывают суточное, а в некоторых случаях и годовое движение. При расчетах движения космических кораблей систему отсчета связывают с Солнцем и так называемыми «неподвижными» звездами.
Для измерения расстояний в пространстве используют единицу длины метр.
Время в механике считают скалярной, непрерывно изменяющейся величиной, одинаковой для всех систем отсчета. За единицу времени принята секунда.
Для характеристики рассматриваемого движения в механике пользуются понятиями «траектория точки», «скорость точки» и «ускорение точки».
Траекторией называют множество последовательных положений движущейся точки в рассматриваемой системе отсчета.
Скоростью точкиназывают пространственно-временную меру, характеризующую быстроту и направление движения точки.
Ускорением точки называют пространственно-временную меру, характеризующую изменение абсолютной величины и направления скорости.
Способы задания движения точки. Определение скорости и ускорения точки. Для задания движения точки в пространстве пользуются каким-либо одним из трех основных способов: векторным, координатным, естественным.
Векторный способ. Положение точки в пространстве однозначно определяется заданием радиуса-вектора  , проведенного из некоторого неподвижного центра О в данную точку М. Для определения движения точки должна быть задана вектор-функция
, проведенного из некоторого неподвижного центра О в данную точку М. Для определения движения точки должна быть задана вектор-функция 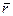 аргумента t (рис. 3.1.47):
аргумента t (рис. 3.1.47):
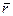 = f(t). (3.1.40)
= f(t). (3.1.40)
Траекторией точки является годограф радиус-вектора.
Вектор скорости точки в данный момент времени t равен первой производной от радиус-вектора точки по времени и направлен по касательной к траектории точки в сторону движения (рис. 3.1.48).
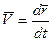 . (3.1.41)
. (3.1.41)
Скорость – это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета. Скорость измеряется в м/с.
Ускорением точки называется вектор, характеризующий быстроту изменения вектора скорости (рис. 3.1.49)
 . (3.1.42)
. (3.1.42)

Ускорение точки равно первой производной от вектора скорости или второй производной от радиуса вектора точки по времени. Вектор ускорения точки всегда направлен в сторону вогнутости траектории и лежит в так называемой соприкасающейся плоскости.
Координатный способ.Рассмотрим движение точки в прямоугольной системе декартовых координат (рис. 3.1.50). Положение точки М в системе отсчета OXYZ определяется тремя декартовыми координатами точки x, y, z:
x = f1(t); y = f2(t); z = f3(t). (3.1.43)
Уравнение (3.1.43) задает движение точки в декартовых координатах. Обозначим орты осей координат за  . Проведем из начала координат в движущуюся точку М радиус-вектор
. Проведем из начала координат в движущуюся точку М радиус-вектор 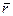 , где
, где  , тогда
, тогда
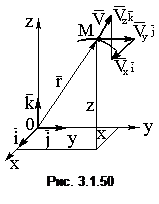
 , (3.1.44)
, (3.1.44)
где Vx =  , Vy =
, Vy =  , Vz =
, Vz =  – проекции вектора скорости точки на неподвижные оси декартовых координат. Модуль и направление вектора скорости
– проекции вектора скорости точки на неподвижные оси декартовых координат. Модуль и направление вектора скорости
V =  =
= 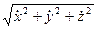 , (3.1.45)
, (3.1.45)


 (3.1.46)
(3.1.46)
Ускорение точки определяем, зная, что
 =
=  =
= 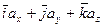 , (3.1.47)
, (3.1.47)
где  =
= 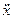 ,
,  =
=  ,
,  =
=  – проекции ускорения на координатные оси.
– проекции ускорения на координатные оси.
Модуль и направляющие косинусы вектора ускорения:
 , (3.1.48)
, (3.1.48)
cos 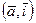 =
=  ; cos
; cos  =
=  ; cos
; cos  =
=  . (3.1.49)
. (3.1.49)
Естественный способ. Движение точки определено, если заданы (рис. 3.1.51):
- траектория, положение которой относительно выбранной системы отсчета известно;
- начало и направление отсчета дуговой координаты;
- уравнение движения
S = f (t), (3.1.50)
связывающее расстояние движущейся точки от начала отсчета со временем. В общем случае расстояние (S) не равно пройденному точкой М пути, так как точка может начать движение не из начала отсчета, а из другого положения (М1). Численное значение скорости определяется по формуле
 , (3.1.51)
, (3.1.51)
т.е. равно первой производной по времени от расстояния.
Знак скорости показывает направление движения точки в данный момент. При знаке «плюс» точка движется в сторону положительного отсчета расстояний и наоборот.
При естественном способе задания движения ускорение точки определяют его составляющими, направленными по так называемым естественным осям. Траектория точки, как и любая кривая, имеет три естественные оси (рис. 3.1.52):
- касательную (орт оси – 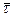 ) – ось, направленная в сторону положительного отсчета;
) – ось, направленная в сторону положительного отсчета;
- главную нормаль (орт оси –  ) – линию пересечения соприкасающейся и нормальной плоскостей, направленную в сторону вогнутости кривой;
) – линию пересечения соприкасающейся и нормальной плоскостей, направленную в сторону вогнутости кривой;
- бинормаль (орт оси – 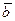 ) – ось, перпендикулярную касательной и главной нормали.
) – ось, перпендикулярную касательной и главной нормали.
Кривизной кривой (K) в данной точке называют предел отношения угла смежности (рис. 3.1.53) к длине дуги ΔS, ему соответствующей, при ΔS→0: K = lim Δφ/ ΔS.
 |
Величина, обратная кривизне K, называется радиусом кривизны:
 .
.
Ускорение точки лежит в соприкасающейся плоскости и равно производной от вектора скорости по времени (рис. 3.1.54).
 Представим вектор скорости
Представим вектор скорости 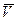 как произведение ее численного значения V на орт касательный
как произведение ее численного значения V на орт касательный  :
:
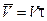 , (3.1.52)
, (3.1.52)
 . (3.1.53)
. (3.1.53)
Первое слагаемое есть касательное ускорение точки, характеризующее изменение вектора скорости этой точки только по модулю:
 . (3.1.54)
. (3.1.54)
Рассмотрим второе слагаемое. Величину |  | найдем, взяв предел отношения │Δτ│ к ∆t при ∆t → 0. Получим
| найдем, взяв предел отношения │Δτ│ к ∆t при ∆t → 0. Получим  , где
, где  – единичный вектор, направленный по главной нормали, ρ – радиус кривизны траектории.
– единичный вектор, направленный по главной нормали, ρ – радиус кривизны траектории.
Тогда  – составляющая ускорения точки вдоль главной нормали к траектории называется нормальным ускорением точки и характеризует изменение направления вектора скорости:
– составляющая ускорения точки вдоль главной нормали к траектории называется нормальным ускорением точки и характеризует изменение направления вектора скорости:
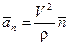 . (3.1.55)
. (3.1.55)
Нормальное ускорение всегда направлено к центру кривизны траектории
Полное ускорение определяется по формуле
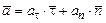 . (3.1.56)
. (3.1.56)
Модуль ускорения и его направление определяют по формулам:
 ; (3.1.57)
; (3.1.57)
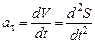 или
или  ,
,  , (3.1.58)
, (3.1.58)
tg α = 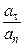 . (3.1.59)
. (3.1.59)
Движение точки будет ускоренным (рис. 3.1.55, а), если направление векторов скорости 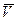 и касательного ускорения совпадает, и замедленным (рис. 3.1.55, б), если наоборот.
и касательного ускорения совпадает, и замедленным (рис. 3.1.55, б), если наоборот.
Прямолинейное равномерное движение точки– единственный вид движения, при котором ускорение точки равно нулю:
V = const;  ρ = ∞;
ρ = ∞;  .
.

Рис. 3.1.55
Прямолинейное неравномерное движение точкихарактеризуется изменением скорости по модулю:
V≠ const;  ; ρ = ∞ ,
; ρ = ∞ ,  = 0;
= 0;  .
.
Криволинейное и равномерное движение точкихарактеризуется изменением направления скорости:
ρ ≠ ∞;  ≠ 0, V = const;
≠ 0, V = const;  ,
,  .
.
Криволинейное неравномерное движение точки:
ρ ≠ ∞; V ≠ const;  ;
;  ;
;  ,
,
dV/dt = at = const; 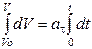 , V = V0 ± att. (3.1.60)
, V = V0 ± att. (3.1.60)
Скорость и уравнение равнопеременного движения точки:
V =  = V0 + att ;
= V0 + att ;  ;
;
S = S0 + V0t ±  . (3.1.61)
. (3.1.61)
Уравнение равнопеременного движения точки при S0 = 0, V0 = 0:
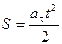 .
.
Пример 1. Посадочная скорость самолета (Vпос) равна 140 км/ч, длина пробега после посадки (L) оставляет 450 м. Найдите время (t) пробега и ускорение (aпос).
Решение. Для определения ускорения самолета используем уравн
Дата добавления: 2014-11-13; просмотров: 459; Мы поможем в написании вашей работы!; Нарушение авторских прав |