
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Законы Ньютона. Принцип относительности Галилея
Чтобы сформулировать законы динамики введем динамические параметры движения:
Силойназывают векторную физическую величину, характеризующую механическое действие одного тела на другое и являющуюся мерой этого воздействия. В результате действия силы тела приобретают ускорение или деформируются, или имеет место и то и другое одновременно. Т.о Следовательно о наличии сил можно судить:
1) по их динамическому проявлению (по ускорению);
2) по статическому проявлению (по деформациям);
Масса – мера количества материи.
Масса тел проявляется в двух свойствах:
1) в свойстве притягивать к себе другие тела (и притягиваться ими) – гравитация.
2) в инерции тел.
Инертность - свойство присущее всем телам обладающим массой. Состоит оно в том, что для изменения скорости тела требуется некоторое время, чем больше это время (при одной и той же силе) тем инертнее тело. Инертность - Свойство материального тела сохранять в отсутствии сил состояние покоя или равномерного и прямолинейного движения.
Масса - мера инертности тел (чем больше масса, тем больше инертность).
Первый закон Ньютона (Закон инерции).
1) Всякое тело, на которое не действуют другие тела или действие других тел скомпенсировано, движется с постоянной скоростью или покоится.
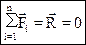
Согласно этому закону силы не являются первопричиной движения. И в отсутствии сил тела движутся. Это инерциальное движение тела.
2) Существуют системы отсчета, называемые инерциальными, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной, если на него не действуют другие тела или равнодействующая сил, действующих на тело, равна нулю.
Если известная хотя бы одна инерциальная система отсчета, существует бесконечное множество других инерциальных систем, движущихся относительно ее равномерно прямолинейно.
Причина изменения скорости движения тела всегда является его взаимодействие с другими телами.
Второй закон Ньютона.
1) ускорение, приобретаемое телом в результате взаимодействия с другими телами, прямо пропорционально равнодействующей сил, действующих на тело, и обратно пропорционально массе тела.
2) Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение.
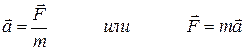
Импульс тела (количество движения) - векторная физическая величина, являющаяся мерой механического движения.
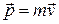
Импульс силы - векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени.
 (более общий вид)
(более общий вид)
 Третий закон Ньютона. Тела действуют друг на друга с силами, направленными вдоль одной прямой, равными по модулю и противоположными по направлению.
Третий закон Ньютона. Тела действуют друг на друга с силами, направленными вдоль одной прямой, равными по модулю и противоположными по направлению.

Пример:а) тело, притягиваясь к Земле, действует на опору – вес тела 
б) на тело со стороны опоры, действует сила реакции  .
.
При взаимодействии тел наблюдается как прямое действие, так и действие на расстоянии.
Принцип относительности Галилея: все инерциальные системы равноправны. Все физические процессы в во всех инерциальных системах протекают одинаково, поэтому невозможно никакими физическими средствами определить движется инерциальная система или покоится.
Принцип независимости действия сил. Ускорение, сообщаемое телом при одновременном действии нескольких сил, равно векторной сумме ускорений, корорые сообщила бы этому телу каждая сила, действующая в отдельности. (решить задачу на наклонную плоскость)
Все силы сводят к 4 фундаментальным взаимодействиям: гравитационное, электромагнитное, слабое взаимодействие, сильное взаимодействие.
Относительное движение.
Инерциальные системы. Механический принцип относительности.
Системы отсчета можно связать как с неподвижными телами отсчета, так и с движущимися.
| Вопрос: | Будут ли законы динамики справедливы в обеих системах отсчета? Какие поправки (к скорости и ускорению) нужны, чтобы законы были справедливы? |
| Пример: | по палубе равномерно и прямолинейно движущегося относительно берега корабля перемещается известным образом тело. Различно ли и как его движение относительно палубы и берега? |
Система отсчета, связанная с палубой – подвижная.
Система отсчета, связанная с берегом – неподвижная.
Движение тела в подвижной системе – относительное движение.
Движение тела в неподвижной системе – абсолютное движение.
Движение тела относительно неподвижной системы отсчета, которым оно обладало бы, будучи жестко связанное одной из точек подвижной, называется переносным движением.

| Имеем две системы: |
a) неподвижную XYZ  подвижнуюX’Y’Z’
подвижнуюX’Y’Z’
| |
| б) X’Y’Z’ перемещается относительно XYZ прямолинейно со v0 вдоль оси х. | |
| в) в начальный момент t = 0 оси обеих систем совпадали. | |
| г) точка М имеет координаты как в подвижной так и в неподвижной системах |
Преобразования ГАЛИЛЕЯ 
Зная, что 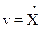 и
и  имеем
имеем
 (4)
(4)
 (5)
(5)
Уравнения (4 и 5) в векторной записи в общем случае:
 (6)
(6)
 (7)
(7)
Из уравнения (7) следует, что ускорение одного и того же тела в каждый момент времени одинаково во всех системах отсчета, движущихся относительно друг друга равномерно и прямолинейно.
Системы отсчета движущиеся относительно неподвижной равномерно и прямолинейно называются инерциальными.
Следовательно, инерциальные системы отсчета образуют замкнутую систему. Инерциальные системы – это абстракция, но практически с большой степенью точности можно считать инерциальной системой отсчета, связанную с центром масс Солнечной системы (гелиоцентрическая). В некоторых задачах за инерциальные могут быть приняты системы, связанные с Землей или телами, движущимися, движущимися относительно Земли равномерно и прямолинейно.
Равенство (7) выражает механический принцип относительности.
| Принцип относительности Галилея | Никаким механическими опытами, произведенными внутри инерциальной системы отсчета, нельзя установить, находится ли она в покое или движется равномерно и прямолинейно. |
Уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой.
| Пример: | чтобы прыгнуть на расстояние 1 метр в направлении кормы корабля или носа при равномерном и прямолинейном его движении, нужно усилие, равное усилию при прыжке на покоящемся корабле. |
Следовательно, при описании движения в неинерциальных системах отсчета можно пользоваться уравнениями динамики, справедливыми только для инерциальных систем, если наряду с силами, обусловленными воздействием тел друг на друга, учитывать силы инерции:

Пример:

| Когда тележка стоит или движется равномерно и прямолинейно P = N и шарик неподвижен относительно тележки. |

| Когда тележка движется с ускорением  , то шарик отклоняется. , то шарик отклоняется.
 – результирующая сил – результирующая сил  обеспечивает ускорение обеспечивает ускорение  шарику.
Так как шарик снова неподвижен, то шарику.
Так как шарик снова неподвижен, то  , т.е. , т.е.

|
Введение сил инерции дает возможность описывать движение тел в любых системах отсчета.
Силы инерции не являются силами воздействия (упругие, гравитационные, трения), они обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления. Силы инерции – фиктивные силы.
Дата добавления: 2014-10-31; просмотров: 674; Мы поможем в написании вашей работы!; Нарушение авторских прав |