Оценка адекватности тренда и прогнозирование

Для найденного уравнения тренда необходимо провести оценку его надежности (адекватности), что осуществляется обычно с помощью критерия Фишера, сравнивая его расчетное значение F_р с теоретическим (табличным) значением F_Т (Приложение 3). При этом расчетный критерий Фишера определяется по формуле (76):

, (76)

где k – число параметров (членов) выбранного уравнения тренда.

Для проверки правильности расчета сумм в формуле (76) можно использовать следующее равенство (77):

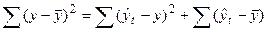. (77)

В нашем примере про ВО равенство (77) соблюдается (необходимые суммы рассчитаны в трех последних столбцах табл. 16): 89410,434 = 9652,171 + 79758,263.

Сравнение расчетного и теоретического значений критерия Фишера ведется при заданном уровне значимости (вероятности сделать неверный прогноз) с учетом степеней свободы: и . При условии F_р > F_Т считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.

Проверим тренд на адекватность в нашем примере про ВО по формуле (76):

F_Р = 79758,263*5/(9652,171*1) = 41,32 > F_Т, значит, модель адекватна и ее можно использовать для прогнозирования (F_Т = 6,61 находим по Приложению 3 в 1-ом столбце [ 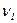= k – 1 = 2 – 1 = 1] и 5-й строке [ = n – k = 5]).

Как уже было отмечено ранее, в нашем примере про ВО России можно произвести выравнивание не только по прямой линии, но и по параболе, чего делать не будем, так как уже найденный линейный тренд адекватно описывает тенденцию.

При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле (78):

, (78)

где 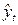– точечный прогноз, рассчитанный по модели тренда; 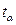– коэффициент доверия по распределению Стьюдента при уровне значимости и числе степеней свободы =n–1 (Приложение 2)[19]; – ошибка аппроксимации, определяемая по формуле (79):

. (79)

Спрогнозируем ВО России на 2007 и 2008 годы с вероятностью 0,95 (значимостью 0,05), для чего найдем ошибку аппроксимации по формуле (79): = = 43,937 и найдем коэффициент доверия по распределению Стьюдента по Приложению 2: 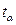= 2,4469 при 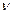= 7 – 1= 6.

Прогноз на 2007 и 2008 годы с вероятностью 0,95 по формуле (78):

Y₂₀₀₇ = (257,671+53,371*4) 2,4469*43,937 или 363,6<Y₂₀₀₇<578,7 (млрд. долл.);

Y₂₀₀₈ = (257,671+53,371*5) 2,4469*43,937 или 417,0<Y₂₀₀₈<632,0 (млрд. долл.).

Как видно из полученных прогнозов, доверительный интервал достаточно широк (из-за достаточно большой величины ошибки аппроксимации). Более точный прогноз можно получить при выравнивании по параболе 2-го порядка.

Дата добавления: 2014-12-23; просмотров: 18; Нарушение авторских прав