Модуль деформаций бетона

Начальный модуль упругости бетона при сжатии 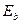соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях . Он определяется в соот­ветствии с законом Гука как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 1.11), т.е.

где р = 1 МПа — масштабно-размерный коэффициент.

Обычно 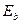определяется из специальных опытов на призмах при низком уровне напряжений ( ), когда бетон можно рассматривать как упругий материал.

При действии на бетон нагрузки, при которой , хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бе­тона 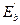становится величиной переменной.

Для расчёта железобетонных конструкций пользуются сред­ним модулем деформаций или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей, проведённой через начало координат и точку на кривой сзаданным на­пряжением, к оси абсцисс, т.е.

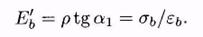
Начальный модуль упругости бетона при растяжении по аб­солютной величине принимается равным 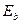, то есть , а

где v_t = 0,15 — значение коэффициента упругопластичности бетона при растяжении в момент, предшествующий разрушению.

Значения модуля сдвига бетона G принимают по установленной в теории упругости зависимости

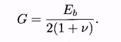
Подставив в неё начальный коэффициент поперечной деформации бетона ν=0,2, получим .