Тема 5: Компьютерное моделирование в экологии.

Экология - одно из слов, появившихся сравнительно недавно у всех на устах и на страницах газет и журналов. Еще в 60-х годах прошлого столетия почти никто, кроме узких специалистов, его не знал, да и большинство из тех, кто знал, использовал в таком смысле, который вряд ли способен заинтересовать широкую общественность. А между тем, термину более 140 лет.

В 1869 г. немецкий естествоиспытатель Эрнст Геккель предложил составной термин «экология» («эко» - дом, жилище, местопребывание и «логос» - наука, знание) как название раздела биологии, ставшего самостоятельным.

Классическая экология - наука о взаимодействии организмов и окружающей среды. Сегодня, говоря об экологии, чаще всего имеют в виду не классическую, а, так называемую, социальную экологию, оформившуюся как научное направление и направление общественно-политической деятельности на 100 лет позднее, и занимающуюся проблемами охраны окружающей среды, взаимодействием с ней человеческого сообщества.

Мы рассмотрим некоторые модели классической «старой» экологии. Нам понадобятся следующие понятия.

Под особью понимается отдельный индивидуум, отдельный организм. Популяция - это совокупность особей одного вида, существующих в одно и то же время и занимающих определенную территорию.

И, наконец, сообщество - это совокупность совместно сосуществующих популяций.

В классической экологии рассматриваются взаимодействиянескольких типов:

• взаимодействие организма и окружающей среды;

• взаимодействие особей внутри популяции;

• взаимодействие между особями разных видов (между популяциями). Математические модели в экологии используются практически с момента возникновения этой науки. И, хотя поведение организмов в живой природе гораздо труднее адекватно описать средствами математики, чем самые сложные физические процессы, модели помогают установить некоторые закономерности и общие тенденции развития отдельных популяций, а также сообществ. Кажется удивительным, что люди, занимающиеся живой природой, воссоздают ее в искусственной математической форме, но есть веские причины, которые стимулируют эти занятия.

Вот некоторые цели создания математических моделей в классической экологии.

1. Модели помогают выделить суть или объединить и выразить с помощью нескольких параметров важные разрозненные свойства большого числа уникальных наблюдений, что облегчает экологу анализ рассматриваемого процесса или проблемы.

2. Модели выступают в качестве «общего языка», с помощью которого может быть описано каждое уникальное явление, и относительные свойства таких явлений становятся более понятными.

3. Модель может служить образцом «идеального объекта» или идеализированного поведения, при сравнении с которым можно оценивать и измерять реальные объекты и процессы.

4. Модели действительномогут пролить свет на реальныймир, несовершенными имитациями которого они являются.

При построении моделей в математической экологии используется опыт математического моделирования механических и физических систем, но учитываются и такие специфические особенности биологических систем, как:

• сложности внутреннего строения каждой особи;

• зависимость условий жизнедеятельностиорганизмов от многих фактороввнешней среды;

• незамкнутость экологических систем;

• огромный диапазон внешних характеристик, при которых сохраняется жизнеспособность систем.

Привлечение компьютеров существенно раздвинуло границы моделирования экологических процессов. С одной стороны, появилась возможность всесторонней реализации сложных математических моделей, не допускающих аналитического исследования, с другой - возникли принципиально новые направления, и прежде всего - имитационное моделирование.

МОДЕЛИ ВНУТРИВИДОВОЙ КОНКУРЕНЦИИ (Одновидовые модели)

В одновидовых моделях рассматривается одна единственная популяция и учитывается взаимодействие ее особей друг с другом и окружающей средой. Взаимодействие с другими популяциями игнорируется. Основная задача – описать изменение численности популяции в зависимости от времени.

Одновидовая модель с дискретным временем.

Предположим, что изменение численности популяции может происходить не непрерывно, т.е. не в любой момент времени, а через какие-то равные промежутки времени. В этом случае используется модель с дискретным временем. Промежутки, через которые происходит размножение, можно считать равными, а соответствующие моменты времени можно занумеровать натуральными числами.

t=0 – момент начала наблюдений, t=1 – время первого изменения численности, t=2 – время второго изменения численности и т.д.

Рассмотрим простейшую из указанных моделей для вида с дискретными периодами размножения, в которой численность популяции в момент времени t равна N_t, и изменяется во времени пропорционально величине основной чистой скорости воспроизводства R. Такими видами являются, например, большая часть растений, некоторые виды насекомых, у которых разные поколения четко разнесены во времени. Коэффициент R характеризует количество особей, которое воспроизводится в расчете на одну существующую, а также выживание уже существующих. Данная модель может быть выражена уравнением

(1)

решение которого имеетвид

(2)

где N₀ - начальная численность популяции.

Эта модель, однако, описывает популяцию, в которой отсутствует конкуренция и в которой R является константой; если R>1, то численность популяции будет бесконечно увеличиваться. В реальности в какой-то момент начинают работать механизмы сдерживания роста популяции. В литературе приводится немало интересных примеров быстрого роста численности популяций, если бы для их размножения существовали идеальные условия. Особенно это относится к насекомым, растениям и микроорганизмам, которые могли бы покрыть земной шар толстым слоем, если им создать благоприятные условия для размножения. Но в действительности такого роста популяций, когда их численность увеличивается в геометрической прогрессии, на сколько-нибудь длительных промежутках времени не наблюдается.

Возможны 3 сценария:

R<1 R=1 R>1

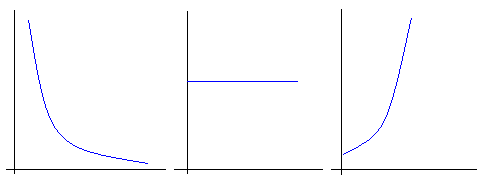
Можно сделать вывод, что в третьем случае и в остальных случаях модель не является адекватной. Мы не учли ограниченность природных ресурсов и внутривидовую конкуренцию.

Изменим нашу модель, чтобы скорость воспроизводства учитывала межвидовую конкуренцию. Следовательно, в первую очередь необходимо изменить уравнение (1) таким образом, чтобы чистая скорость воспроизводства R зависела от внутривидовой конкуренции.

Конкуренцию можно определить как использование некоего ресурса (пищи, воды, света, пространства) каким-либо организмом, который тем самым уменьшает доступность этого ресурса для других организмов. Если конкурирующие организмы принадлежат к одному виду, то взаимоотношения между ними называют внутривидовой конкуренцией, если же они относятся к разным видам, то их взаимоотношения называют межвидовой конкуренцией.

Рис. К вопросу об ограничении скорости роста популяции

На рис. показана простейшая возможная зависимость скорости воспроизводства от численности популяции. Точка А отражает ситуацию, в которой численность популяции близка к нулю, конкуренция при этом практически отсутствует, и фактическую скорость воспроизводства вполне можно описывать параметром R в его первоначальном виде. Следовательно, при низкой плотности популяции уравнение (1) вполне справедливо. В преобразованном виде оно выглядит так:

Точка В, напротив, отражает ситуацию, в которой численность популяции высока, и в значительной степени проявляется внутривидовая конкуренция. Фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может не более чем восстанавливать в каждом поколении свою численность, потому что количество родившихся особей уравновешивается количеством погибших. Гипотезе, отраженной на нашем рисунке, соответствует уравнение

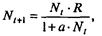(3)

где . Это уравнение представляет собой модель роста популяции, ограниченного внутривидовой конкуренцией. Суть этой модели в том, что константа R в уравнении (1) заменена на фактическую скорость воспроизводства, т е. , которая уменьшается по мере роста численности популяции N_t. Достоинство полученного уравнения заключается в его простоте. Такой тип конкуренции приводит к саморегуляции численности популяции, изображенной на рис. (для некоторого набора параметров модели; численное решение).

Рис. Изменение численности популяции согласно уравнению (3)

при R = 2, К = 200, N₀ = 20

После несложного изменения в уравнении (3) может быть получена гораздо более общая модель, учитывающая интенсивность конкуренции. Простейшая из возможных зависимостей падения скорости роста популяции от ее численности, изображенная на предыдущем рисунке, является не законом природы, а всего лишь удобной гипотезой. Далеко не всегда реальная динамика численности популяции, определяемая внутривидовой конкуренцией, даже качественно согласуется с изображенной на последнем рисунке. Более общая гипотеза о законе падения скорости роста популяции в зависимости от ее численности приводит к следующему уравнению:

(4)

Общность данной модели в отличие от уравнения (3) обусловлена введением в модель параметра b, который определяет тип зависимости падения скорости роста популяции от ее численности.

Набор величин a, b, R можно использовать для сравнения и противопоставления сильно различающихся ситуаций. Другим положительным качеством уравнения (4) является его способность освещать новые стороны реального мира. Путем анализа кривых динамики популяций, полученных с помощью уравнения, можно прийти к предварительным выводам относительно динамики природных популяций.

На следующих рисунках а, б, в и г, построенных с помощью численного моделирования, показаны различные варианты динамики численности популяций, полученные с помощью уравнения (4) при разном сочетании параметров b и R.

Рис. а. Монотонное установление стационарной численности популяции

при b =1,4, R =2

Рис. б. Колебательное установление стационарной численности популяции

при b =3,9, R =2

Рис. в. Устойчивые предельные циклы изменения численности популяции

при b = 3,6, R = 4

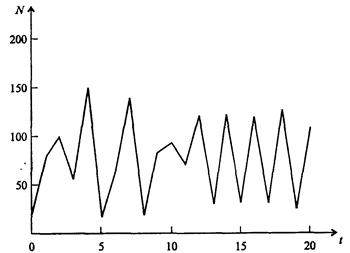
Рис. г. Случайные изменения численности популяции при b = 4,4, R = 4

В связи с уравнениями (3), (4) сделаем замечание общего характера, справедливое для всех моделей в экологии. В отличие от физики, где «модель» часто является точно установленным законом природы, в экологии модель гораздо более условна. Ее адекватность реальности (в той мере, в какой моделирование вообще на это претендует) проверяется лишь экспериментально. Поскольку экологи много раз наблюдали каждую из динамик, изображенных на этих четырех рисунках, можно сделать вывод о полезности соответствующей модели (иначе она была бы лишь математическим упражнением).

Важной частью исследования, связанного с моделью (4), является построение на фазовой плоскости (b, R) границ, которые разделяют монотонное затухание, затухающие колебания, устойчивые предельные циклы и случайные (хаотические) изменения, см. следующий рис. Для этого надо задаться значениями а и N₀ и производить расчеты, изменяя параметры b, R. Различить каждый из возможных режимов можно попытаться визуально, выполняя построение на экране компьютера графиков изменения численности популяции и запоминая соответствующие значения параметров b, R при переходе от одного режима к другому. Следует, однако, понимать, что установление различий между квазипериодическими, апериодическими и хаотическими движениями - сложная математическая задача. Для ее решения используются методы преобразований Фурье и другие.

Рис. Схематическое изображение фазовой диаграммы динамики численности популяции с дискретным размножением

Рассмотрим теперь модель с непрерывным временем.

До сих пор мы рассматривали модели, применимые к популяциям с дискретными периодами размножения. Но в природе встречаются и популяции, где рождение и гибель организмов происходит непрерывно; для таких популяции модели, выраженные уравнениями из предыдущего пункта, непригодны. Рассмотрим популяцию с непрерывным размножением и построим модель изменения ее численности. Математическим аппаратом здесь являются дифференциальные уравнения.

Вначале попробуем обойтись без учета внутривидовой конкуренции. При отсутствии конкуренции скорость изменения численности прямо пропорциональна самой численности:

Скорость роста в этом случае можно обозначить , тогда средняя скорость увеличения численности в расчете на одну особь определяется величиной .

Без учета внутривидовой конкуренции получаем =rили

(5)

Через r обозначена мгновенная удельная скорость роста численности, т.е. приращение численности за единицу времени в пересчете на одну особь. Согласно этой модели, вследствие того, что не учтена внутривидовая конкуренция, численность популяции при r > 0 будет неограниченно возрастать, т.е. будет наблюдаться экспоненциальный рост.

Чтобы решить уравнение (5), необходимо задать начальные условия: численность популяции в нулевой момент времени.

N(0)=N₀

N(t)=N₀∙e ^{r· t}.

В зависимости от r возможны 3 сценария изменения численности популяции:

r<0 r=0 r>0

Из графиков можно сделать вывод, что модель не является адекватной, и нужно учитывать внутривидовую конкуренцию. Для этого воспользуемся методом, который однажды уже применяли (см. рис. А-В).

Рис. Зависимость скорости воспроизводства от численности популяции

Если численность популяции мала, то конкуренции нет и можно пользоваться уравнением (5), скоростьростаопределяется величиной r, так как конкуренция еще не оказывает влияния на прирост популяции. На графике этой ситуации соответствует т. А.

Когда же при возрастании N достигается значение K (предельной плотности насыщения), скорость роста популяции снижается до нуля (точка В), численность дальше возрастать не может из-за большой конкуренции. Простейший способ получить интересующую нас закономерность – построить прямую АВ. Рассматривая уравнение этой прямой, получаем закономерность:

(6)

Начальное условие по-прежнему имеет вид N(0)=N₀.

Последнее уравнение (6) известно под названием «логистического». Одно из его достоинств - простота. Уравнение относится к одному из стандартных типов и допускает аналитическое решение:

(7)

В истории экологии логистическое уравнение сыграло значительную роль, оказав большое влияние на применение в экологии математических методов. С другой стороны, простота уравнения накладывает ограничения на область его применения, так как с его помощью можно описать немногие реальные популяции. Но, несмотря на все ограничения, логистическое уравнение используется как составная часть и в других моделях динамики численности популяции, рассматриваемых ниже.

Изменение численности популяции в соответствии с формулами (6)-(7) иллюстрирует рис.

Рис. Динамика численности популяции при No =25, К = 200, r = 3