
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычислительный процесс разветвляющейся структуры
Вычислительный процесс называется разветвляющимся, если возникает необходимость в зависимости от выполнения или не выполнения некоторых условий осуществить то или иное действие, т.е. реализовать одну из ветвей вычислительного процесса .
Разветвляющийся процесс имеет некоторые структурные разновидности:
1. Разветвление.
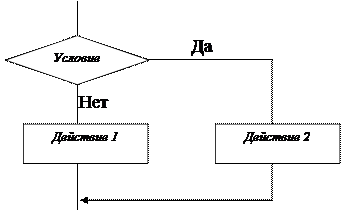
Рис. 5
Применяется, когда в зависимости от условия выполняется одно или другое действие. Причем действие 1 или действие 2 может содержать несколько этапов.
2. Обход.
Частный случаи разветвления, когда одна ветвь не содержит вообще никаких действий.

Рис. 6
3. Множественный выбор
 |
А=1 А=2 А=3 ... А=N
…
Рис. 7
Обобщенный случай разветвления, когда, в зависимости от значений переменной А, выполняется одно из некоторых действий.
Пример 2.
| Вычислить Y = |  a sin x если х >2 a sin x если х >2
|
| в cos x если x £ 2 |

да
Рис. 8
Пример программы:
input a,b,x
if x>2 then
y=a*sin(x)
else
y=b*cos(x)
end if
print y
end.
Если при вводе переменной x будет присвоено значение, большее двух, то будут выполнены блоки 1, 2, 4, 5. В противном случае выполнятся блоки 1, 2, 3, 5.
 Пример 3.
Пример 3.
Вычислить 1, если x > 0
Y = 0, если x = 0
-1, если x < 0
В данном примере заданы три различных условия. Если будет введено значение х > 0 , выполнятся блоки 1, 2, 6, 7 /рис. 9/. В противном случае (при невыполнении условия х > 0) еще нельзяопределить, какоезначение будет присвоено Y, т.к. необходимо разделить случаи: х > 0 и х = 0. Это делается в блоке 3. Только после проверки условия блока 3 становится ясно, какое значение будет присвоено переменной Y. Если х = 0 , выполняется блок 5, иначе выполняется блок 4. В данном варианте алгоритма проверку условия x < 0 производить не следует, т.к. после блока 3 линия “нет” определяет это условие.

x < 0
x £ 0
Рис.9
Пример программы:
input x
if x>0 then
y=1
elseif x=0 then
y=0
else
y=-1
end if
print y
end.
Пример 4.
 Определить, принадлежит ли точка М/х,y/ заштрихованной области Д.
Определить, принадлежит ли точка М/х,y/ заштрихованной области Д.
Y
М/х,y/
x
Рис.10
Математическая постановка.
Радиус круга определяется из формулы  . В соответствии с этим задача сводится к проверке условия
. В соответствии с этим задача сводится к проверке условия
 .
.
Точка М/х,y/принадлежит обл. Д, если  .
.
Точка М/х,y/непринадлежит обл. Д в противном случае.
Блок-схема алгоритма решения задачи представлена на рис. 11
 |
Рис.11
Пример программы:
input x,y
r=sqrt(xÙ2+yÙ2)
if r>=1 and r<=2 then
print “т.М принадлежит обл D”
else
print “т.М не принадлежит обл D”
end if
end.
Примечание. Как отмечалось выше, алгоритм обычно ориентируют на определенный язык программирования. В данном алгоритме проверка условия проведена в двух блоках / 3 и 4 /, т.к. ориентация в данном случае идет на Бейсик стандартный, в котором не реализуется проверка двойного условия.
В языке QBasic, например, это возможно и тогда вместо блоков 3 и 4 можно было бы в алгоритме использовать один блок проверки условия (рис 12). Такое действие реализовано в приведённом алгоритме.

Рис.12
Пример 5.
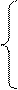
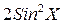 , если
, если 
Вычислить Y = 0.7 – tg X, если 
Не определены в противном случае
В данном примере “У” вычисляется в интервале значений х = [3, 9], при значениях х<3 и x>9 значение “У” не вычисляется. В этом случае в алгоритме должна быть предусмотрена печать сообщения об этом. Это может быть такой текст “при данном значении х значение у не вычисляется “, либо просто может быть выведено на печать значение “х,” по величине которого пользователь программы поймет, что вычисления не производились (рис. 13). Для удобства написания программы на языке стандартного Бейсика удобно так оформлять блок – схемы, чтобы вход очередного логического блока был соединен с линией “нет” предыдущего логического блока. Исходя из этого, начнем проверку с условия “х<3”.

Рис. 13
Пример программы, написанной на языке Q BASIC:
begin
input x
if x>=3 and x<=7 then
y=2*(sin(x)Ù2)
elseif x>=7 and x<=9 then
y=0.7-tan(x)
else
print “y не определён при x=”;x
goto M
end if
print y,x
m: end.
В приведенной программе блоки 2,3 и блоки 3,4 объединены в условие x>=3 и x<=7 и условие x>=7 x<=9.
Программа может быть составлена и без оператора goto M.
Пример 6.
Даны два числа А и В. Если А>В, вычислить их квадраты и записать новые значения на место прежних. Вывести на печать значения А и В.
 |
|

Рис. 14
Программа на Qbasic имеет вид:
input a,b
if a>b then
a=aÙ2; b=bÙ2
end if
print a,b
end.
Блок-схема задачи приведена на рис. 14
В данном примере использована структура «обход». По линии «нет» никаких действий не производится.
Пример 7.

 + 1/(x – 1) , если 3
+ 1/(x – 1) , если 3  Х
Х  5
5
Вычислить У =
6.5х + 9  , если 5 < X
, если 5 < X  7 или X<3
7 или X<3
2 Sin х , если x>7

Рис.15
Пример программы:
input x
if x<3 then
y=6.5+9*xÙ2
elseif x<5 then
y=sqr(x-1)+1/(x-1)
elseif x<7 then
y=6.5+9*xÙ2
else
y=2*sin(x)
end if
print y
end
В данном примере в блоках 6 и 8 “Y” вычисляется по одной и той же формуле. С позиций структурного программирования такая структура более просто реализуется на алгоритмическом языке, чем структура, в которой используется один вычислительный блок при вычислении разных условий /x< 3 5 < x£ 7 \. Такой стиль построения алгоритма сохраняет простоту структуры алгоритма, позволяет легко реализовать соответствующую программу, сделать программу легко читаемой.
2.2.3.Вычислительный процесс циклической структуры.
Вычислительный процесс, многократно повторяющийся при изменении значений некоторых переменных при каждом повторении, называется циклическим или циклом.
Последовательность действий, которая многократно выполняется в цикле, называется телом цикла. Для выполнения тела цикла необходимо определенным образом задавать значения тех переменных, которые изменяются в цикле. Выход из цикла осуществляется при выполнении некоторого условия. Это может быть достижение переменной цикла ее конечного значения, либо достижение заданной точности вычислений.
В различных языках программирования проверка условия выхода из цикла может осуществляться либо до выполнения тела цикла (цикл с предусловием), либо после его выполнения (цикл с постусловием). В соответствии с вышеизложенным циклический процесс можно изобразить двумя вариантами(рис.16, 17).
Цикл с постусловием Цикл с предусловием
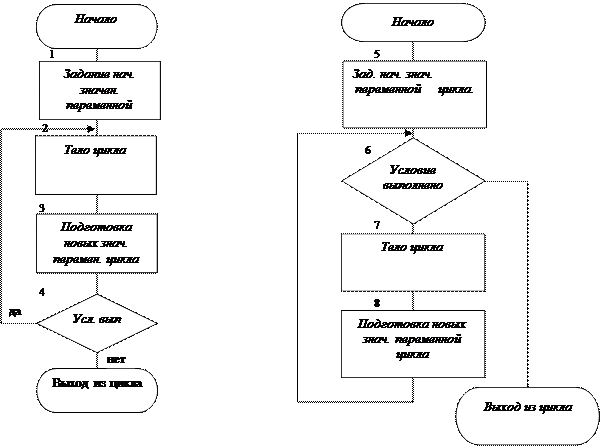

Рис.16 Рис. 17
Тело цикла может иметь различную структуру. Это может быть линейный или разветвляющийся процесс, а также и цикл, в котором тоже должны быть выполнены все перечисленные этапы, циклы такой структуры иногда называют «цикл в цикле » или «вложенные циклы». При подготовке новых значений переменной цикла обычно используют рекуррентное соотношение, которое определяет формулу получения нового значения переменной на основе ее предыдущего значения.
Например: Х = Х + DХ
 и т.д.
и т.д.
Если конечное значение переменной цикла в задаче определено, то при заданном шаге вычислений количество повторений в цикле может быть вычислено по следующей формуле:
N = (Xк - Хн) / D Х + 1,
т.е. число повторений известно. Такие циклы носят название циклов с известным числом повторений. Однако не всегда такое число можно рассчитать, т.к. в некоторых задачах конечное значение переменной цикла неизвестно и выход из цикла осуществляется по выполнении некоторого условия /цикл типа “пока”/. Подобного рода циклы встречаются при решении задач численными методами и называются итерационными циклами или циклами с неизвестным числом повторений.
Циклы с известным числом повторений
Типичным примером арифметического цикла является алгоритм табулирования функции.
Пример 8.
Вычислить значения функции y = x – sin(x) для всех x Î [xн,хк]; шаг изменения аргумента х равен Dх; хн и хк соответственно начальное и конечное значение аргумента х.
Блок-схема алгоритма решения задачи представлена на рис. 18.
 Блок 1. Переменным хн, хк и х задаются их числовые значения путем ввода, например, с пульта дисплея.
Блок 1. Переменным хн, хк и х задаются их числовые значения путем ввода, например, с пульта дисплея.
Блоки 2, 6. Непосредственно циклическая часть задачи. Тело цикла – это линейный процесс /блоки 3, 4/. В блоках 2 и 5 задаются соответственно начальное значение переменной цикла и ее последующие значения. В блоке 6 проверяется условие выхода из цикла.
Другая форма структуры алгоритма этой задачи представлена на рис. 19. Здесь блок проверки условия выхода из цикла расположен сразу после задания переменной цикла.

Рис. 18 Рис. 19
Программа для решения примера, блок-схема алгоритма которого приведена
| На рис.18 | На рис.19 |
| input xн, xk, Dx x=xн m:y=x-sin(3.14*x)^2 print x,y x=x+Dx if x<xк then goto M end | input xн, xk, Dx x=xн m: If x<xк then y=x-sin(3.14*x)^2 print x,y x=x+Dx goto M end if end |
Используя оператор цикла программа может быть записана как
input xн, xk, Dx
for x=xн to xk step Dx
y=x-sin(3,14*x)^2
print x,y
next x
end
Рассмотрим пример циклического процесса, в котором тело цикла является вычислительным процессом разветвляющейся структуры.
Пример 9.
Вычислить значения
 3 cos x , если 2
3 cos x , если 2  x < 3
x < 3
y =
2 sin x , если 3  x
x  5
5
Для всех значений х Î [2,5] с шагом изменения аргумента Dх.
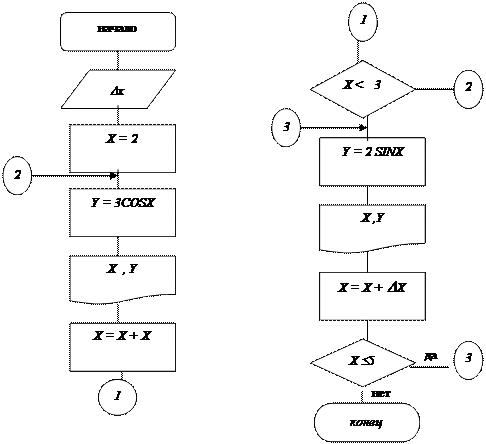 Алгоритм решения данной задачи может иметь структуру, представленную на рис. 21.
Алгоритм решения данной задачи может иметь структуру, представленную на рис. 21.
Рис.21
Пример программы:
input Dx
x=2
1: y=3*cos(x)
print x,y
x=x+Dx
if x<3 then goto 1
2: y=2*sin(x)
x=x+Dx
if x<=5 then goto 2
end
В данном алгоритме два последовательно расположенных цикла. В первом цикле табулируется функция Y = 3cos X на интервале ХС [2, 3] с шагом Х.. Это происходит в блоках 2 ¸ 6 . Второй цикл включает блоки 7 ¸ 11 и в нем происходит табулирование функции y = 2 sin x на интервале x [3 +Dx, 5 ]. Однако такой алгоритм неэффективен с точки зрения повторов однотипных действий в одном и другом циклах. Избежать этого можно, применив для решения задачи алгоритм, представленный на рис. 21.
В данном алгоритме при вычислении функции y = 3 cos x будут «работать» блоки 1,2,3,5,6,7,8. Тело цикла включает блоки 3,4,5,6 и является процессом разветвляющейся структуры.
 |



Рис. 21
Пример программы, где использован оператор цикла:
input Dx
for x=2 to 5 step Dx
if x<3 then
y=3*cos(x)
else
y=2*sin(x)
end if
print x,y
next x
end
Пример 10.
Пусть та же задача поставлена в общем виде. Вычислить
 |
3 cos x , если a < x < в
Y =
2 sin x если в < x < c, где a < c
для всех значений x [ a, c ] шагом Dх. Тогда свойство массовости алгоритма будет выполнено.
 | |||
 | |||


Рис. 22
Пример программы
input a,b,c, Dx
for x=a to c step Dx
if x<b then y=3xCos(x)
else y=2xSin(x)
print x,y
end if
next x
end.
Рассмотрим пример, когда телом цикла является также циклический процесс.
Пример 11.
Вычислить Z = cos x y для каждого x [ xн, xк ] с шагом D x и
X + y
каждого y [ yн, yк ] с шагом D y.
Для наглядности процесса вычислений результаты вычисления могут быть представлены в таблице.
Таблица 3
| X | x1=xн | X1 | X1 | X1 | X2 | X2 | X2 | X2 | … | Xк | Xк | … | Xк | |||
| y | y1=yн | Y2 | … | Yк | Y1 | Y2 | … | Yк | … | Y1 | Y2 | … | Yк | |||
Переменная «х» принимает новое значение только тогда, когда «y» изменит все свои значения от yн до yк. Причем, при новом значении «х» переменная «y» опять изменяется на интервале yн, yк. Блок-схема алгоритма задачи представлена на рис. 23.

Рис. 23
Пример программы:
input xн, xк, Dx, yн , yк , Dy
for x= xн to xк step Dx
for y= yн to yк step Dy
z=cos(x+y)/(x+y)
print x,y,z
next y
next x
end
Блоки 2+9 составляют внешний цикл, блоки 3 + 8 являются телом внешнего цикла и одновременно являются циклом, который называется внутренним.
Выше уже упоминалось понятие рекуррентного соотношения и его использование в циклических процессах для получения нового значения переменной цикла. Рекуррентное соотношение также применяется в циклических структурах в качестве тела цикла при вычислении суммы или произведения, определения максимального или минимального значения из ряда чисел.
Пример 12.
Вычислить сумму N слагаемых 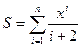
Раскроем эту запись 
Процесс вычисления суммы на ЭВМ представляется как циклический процесс накопления суммы. Причем, каждый новый повтор вычислений в цикле добавляет в ячейку суммы еще одно слагаемое. Используя правило записи рекуррентного соотношения, вычисления тела цикла можно записать в виде следующего соотношения:

Для выполнения тела цикла первый раз необходимо задать начальные значения переменной s и i :
s = 0,
i = 1.
Блок-схема алгоритма представлена на рис. 24.
Примечание. Здесь и в дальнейшем мы будем использовать алгоритмы циклической структуры с постусловием, т.е. блок проверки условия выхода из цикла мы будем размещать после блока подготовки новых значений переменной цикла.
Пример 13.
Вычислить произведение 
Рекуррентное соотношение для вычисления тела цикла 
Начальное значение Р = 1; к = 1. Алгоритм задачи представлен на рис. 25

Рис. 24 Рис. 25
| Программа на Qbasic для задачи рис 24: rem вычисление суммы input n,x s=0 for i=1 to n s=s+xÙi/(i+2) next i print S end | Программа на Qbasic для задачи рис 25: rem вычисление произведения input m,x p=1 for k=1 to m p=p*kÙ2/(k+1) next k print p end |
Пример 14.
Табулировать функцию у =F(x) на интервале Х Î[Xн ,Xк] c
шагом DХ определить ее наибольшее и наименьшее значения на этом отрезке.
Математическая постановка задачи
Определить МАХ = 
МIN =  , где Х Î[Xн ,Xк]
, где Х Î[Xн ,Xк]
Таким образом, после выхода из цикла значение переменной МАХ должно быть равно большему из всех значений функции y(x) на заданном отрезке, а значение переменной МIN соответственно меньшему.
При каждом очередном выполнении цикла сравниваются значения двух пар переменных: Н и МАХ; У и МIN
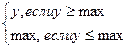
МАХ = /1/

МIN = /2/
Для выполнения первого цикла значения переменных МАХ и МIN уже должны быть определены. Это может быть начальное значение функции У н =f(xн)
МАХ =F(Xн)
МIN =F(Xк)
Однако чаще в качестве начальных значений переменных МАХ и МIN берутся числа заведомо меньшее /для МАХ/ или большее /для МIN/, чем начальное значение функции. Пусть, например, МАХ = -1020 , МIN = 1020 . Тогда при первом же сравнении значения У(Хн) будет присвоено в соответствии с формулами /1/ и /2/ переменным МАХ и МIN. Блок-схема алгоритма решения данной задачи представлена на рис. 26.
Циклы с неизвестным числом повторений
Типичным примером интерационного цикла служат задачи вычисления с заданной точностью.
Итерационные циклы широко используются в численных методах решениях алгоритмических и трансцендентных уравнений, при вычислении интегралов, определении суммы бесконечного ряда и т.д. Во всех этих задачах вычисления прекращаются при достижении некоторой точности (результатов).
Рассмотрим пример вычисления суммы бесконечного ряда чисел.
Пример 15.
Вычислить значение sin x по формуле
SinX = 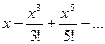
 Блок – схема алгоритма определения максимального и минимального значения функции
Блок – схема алгоритма определения максимального и минимального значения функции
Рис.26
Пример программы:
rem вычисление max,min функции
input Хн, Xк, Dх
max=-10Ù10
min=10Ù10
for x= Хн to Xк step Dx
y=F(x)
print x,y
if y>=max then max=y
if y<=min then min=y
next x
print max,min
end
В операторе y=F(x) в правой части уравнения должно быть записано арифметическое выражение (по условию задачи).
Общая формула члена ряда  где n – номер члена ряда n
где n – номер члена ряда n 
Вычисления продолжать до тех пор пока  >E, это
>E, это 
 условие и есть условие выхода из цикла, где Е – точность вычислений.
условие и есть условие выхода из цикла, где Е – точность вычислений.
При достаточно большом n возведение в степень занимает значительное машинное время . Поэтому каждый член ряда следует получать в соответствии с рекуррентным соотношением
R = Rx 
Где n = 3,5,7……..; R начальное = х. Тогда рекуррентное соотношение для получения суммы ряда будет S = S+R (-1), где Sначальное= Х. Блок – схема алгоритма вычисления суммы ряда представлены на рисунке 27.
Вычисления ведутся до тех пор , пока величина члена ряда R не станет меньше , либо равной некоторой малой величине Е. Значение R с каждым циклом уменьшается. После выполнения цикла первый раз имеем
R = 
S = 
После выполнения цикла второй раз
R = 
S = 
И т.д.
 Структурный подход предполагает использование простейших структур, перечисленных и списанных выше, для построения блок – схемы алгоритмов любой сложной задачи. Рассмотрим это на примере.
Структурный подход предполагает использование простейших структур, перечисленных и списанных выше, для построения блок – схемы алгоритмов любой сложной задачи. Рассмотрим это на примере.
Рис.27
Программа на Qbasic имеет вид:
input x,e
s=x
r=x
n=3
do while r>e
r=r*xÙ2/((n-1)*n)*(-1)
s=s+r
n=n+2
loop
print s
end
Пример 16.
Для каждого значения Х Î[Xn ,Xk] c шагом DХ и для каждого УÎ[Yn, Yk] с шагом DУ определить:


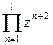 если Z³ 3,5
если Z³ 3,5
W =
Z + 0.7 tgz если Z <3,5
Определить наибольшее и наименьшее значения из всех вычисленных значений W и соответствующие ему значения Х и У.
Блок – схема алгоритма задачи представлена на рис. 28.
Блок 1– ввод исходных данных
Блок 2 – подготовка начальных значений переменных MAX и MIN.
Блоки 3 + 31 = внешний цикл , переменная цикла Х. Тело этого цикла составляют блоки 4+ 30.
Блоки 3, 4, 31 – определяют интервал изменения переменной Х.
Блоки 7-29 – тело внутреннего цикла , переменная цикла У.
Блоки – 5, 6, 30 – определяют интервал изменения переменной У.
Блоки 7+17 – определение значений переменной Z. Это два последовательно расположенных друг за другом цикла, в которых определяется последовательно значения слагаемых 51 и 52, входящих в формулу определения Z.
Блоки 19-25 – определение и печать значения W.Это разветвляющийся вычислительный процесс, одной из ветвей которого (блоки 19-23) является циклический процесс накопления произведения.
Блоки 26 - 29 – определяют наибольшее и наименьшее значения переменной W и ее координаты.
Одним из приемов разработки алгоритмов решения более сложных задач является метод пошаговой детализации . метод пошаговой детализации заключается в том , что первоначально продумывается общая структура алгоритма без детальной проработки отдельных ее частей, , но при этом также используются основные виды структур алгоритмов. Обычно блоки, требующие дальнейшей детализации, обозначают пунктирной линией. Далее они детализируются на следующем шаге и так, пока не будет полностью осуществлена детализация всех блоков. Такой метод называется программированием сверху вниз. Так, блок – схему алгоритма (рис. 28) можно получить, используя метод пошаговой детализации (рис. 29).
 Блок – схема для решения задачи 16.
Блок – схема для решения задачи 16.
 | |||
 |
Рис. 28
 Первый шаг.
Первый шаг.
 |

Рис. 29
Второй шаг.
Детализируем вычисление блоков 7 и 8 блок – схемы рис. 30,31
Блок 7: вычисление Z
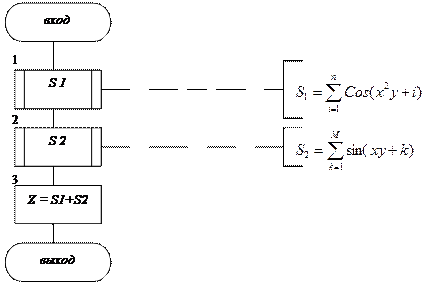 |
Рис.30
Блок 6: вычисление W
 |
Рис.31
Третий шаг.
Детализация блоков 1 и 2 блок – схемы рис. 30.
 |
Детализация блока 1
Детализация блока 2
Рис.32
Детализация блока 3 рис.31
 |
Рис.33
После такой пошаговой детализации мы и получим подробную блок – схему алгоритма решения задачи, представленную на рис. 28.
Программа для решения примера имеет вид:
rem сложный цикл
input n,m,l, Xн ,Xк , Dx, Yн , Yк , Dy
max=-10Ù10 : min=10Ù10
for x= Xн to Xк step Dx
for y= Yн to Yк step Dy
s1=0
for i=1 to n
s1=S1+cos(x*y+i)
next i
s2=0
sor k=1 to m
s2=S2+sin(x*y+k)
next k
z=S1+S2
if z>=3.5 then
w=1
for n=1 to l
w=W*zÙ(n+2)
next n
else
w=z+0.7*tan(z)
end if
print w,x,y,z
if W>=max then
max=w
xmax=x
ymax=y
end if
if W<=min then
min=W
xmin=x
ymin=y
end if
next y
next x
print max, xmax, ymax
Print min, Xmin, Ymin
end
Дата добавления: 2015-01-01; просмотров: 1542; Мы поможем в написании вашей работы!; Нарушение авторских прав |