
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условия на границе раздела двух диэлектриков.
| №п/п | Задания | Ответы | |
| Раздел: ЛИНЕЙНАЯ АЛГЕБРА. | |||
| Тема 1.1: Определители-1:Определители второго, третьего и четвёртого порядков, миноры и алгебраические дополнения элементов. | |||
| 1. | Определитель  равен…
Записать ответ. равен…
Записать ответ.
| -5 | |
| 2. | Дан определитель  . Тогда минор . Тогда минор  элемента элемента  равен…
Записать ответ. равен…
Записать ответ.
| -3 | |
| 3. | Дан определитель  . Тогда алгебраическое дополнение . Тогда алгебраическое дополнение  элемента элемента  равно…
Записать ответ. равно…
Записать ответ.
| -17 | |
| 4. | Определитель  равен:
1) равен:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 2) | |
| 5. | Определитель  равен… равен…
| ||
| 6. | Дан определитель  . Указать все пары, соответствующих друг другу элементов . Указать все пары, соответствующих друг другу элементов  определителя и их алгебраических дополнений определителя и их алгебраических дополнений  : :
   
    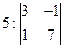 
| 1-2 2-4 3-6 4-3 | |
| Тема 1.2: Определители-2:Вычисление определителей четвёртого порядка. Ранг матрицы и его вычисление. | |||
| 1. | Определитель  равен… равен…
| ||
| 2. | Определитель  равен…
1) равен…
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 2) 
| |
| 3. | Ранг матрицы  равен равен  1)
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 3) 
| |
| Тема 1.3: Матрицы-1:Операции над матрицами (сложение, вычитание, умножение на число, умножение на матрицу, транспонирование). Вычисление определителя матрицы 2-го порядка. | |||
| 1. | Матрица С=АВ+2АТ , где  , ,  , имеет вид , имеет вид  , где , где  , ,  .
Ответ записать в виде: .
Ответ записать в виде: 
| 
| |
| 2. | Если  , , 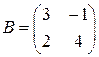 , то матрица , то матрица  равна……
1) равна……
1)   2) 2)  3) 3)  4) 4)  5) 5) 
| 2) | |
| 3. | Пусть  , где , где  , ,  . Тогда определитель . Тогда определитель  матрицы С равен… матрицы С равен…
| 
| |
| Тема 1.4: Матрицы-2:Операции над матрицами (сложение, вычитание, умножение на число, умножение на матрицу, транспонирование). Нахождение обратной к матрице 3-го порядка. | |||
| 1. | Матрица  имеет вид имеет вид  , где , где  , ,  , ,  Ответ записать в виде:
Ответ записать в виде: 
|

| |
| 2. | Матрица  , является обратной к матрице , является обратной к матрице  . Тогда . Тогда  , ,  , ,  Ответ записать в виде:
Ответ записать в виде: 
| -5,-18,0 | |
| Тема 1.5: СЛАУ-1:Системы линейных алгебраических уравнений, методы их решения (методы Крамера и Гаусса). | |||
| 1. | Пусть  - решение системы линейных уравнений - решение системы линейных уравнений  , найденное по формулам Крамера. Тогда , найденное по формулам Крамера. Тогда   , где , где  ( (  целое число).
Ответ записать в виде: целое число).
Ответ записать в виде: 
| ||
| 2. | Набор  значений неизвестных значений неизвестных  является решением невырожденной системы уравнений является решением невырожденной системы уравнений  ,если ,если  , ,  , ,  Ответ записать в виде:
Ответ записать в виде: 
| 
| |
| Тема 1.6: СЛАУ-2:Координаты вектора в произвольном базисе, их вычисление. Матричные уравнения, их решение методом обратной матрицы. | |||
| 1. | Решением матричного уравнения  является матрица является матрица  , где , где  , ,  , ,  .
Ответ записать в виде: .
Ответ записать в виде: 
| 3,0,-2 | |
| 2. | Решением матричного уравнения  является матрица является матрица  , где , где  , ,  .
Ответ записать в виде: .
Ответ записать в виде: 
| 20,-8 | |
| 3. | Вектор  в произвольном базисе в произвольном базисе  , где , где  , ,  , ,  , имеет координаты , имеет координаты  , где , где  , ,  , ,  Ответ записать в виде
Ответ записать в виде  . .
| 1,1,1 | |
| Раздел: ВЕКТОРНАЯ АЛГЕБРА. | |||
| Тема 2.1: Векторы-1. Координаты вектора, его длина. Деление отрезка пополам. Расстояние между точками. Проекция вектора на вектор. Скалярное произведение. Угол между векторами (косинус). Векторное произведение. Площадь треугольника и параллелограмма, объём пирамиды (закрытая форма). | |||
| Тема 2.2: Векторы-2. Длина вектора. Угол между векторами (синус). Векторное произведение, его модуль. Принадлежность четырёх точек одной плоскости. Площадь треугольника и параллелограмма, объём тетраэдра (открытая форма). | |||
| Тема 2.4: Векторы (теория-2). Компланарность, коллинеарность, ортогональность, равенство векторов. | |||
| 1. | Векторы  , ,  и и  будут компланарными, если параметр будут компланарными, если параметр  равен… равен…
| 
| |
| 2. | Ортогональными из векторов  , ,  и и  являются:
1) являются:
1)  2) 2)  3) 3)  4)все 5)ортогональных нет 4)все 5)ортогональных нет
| 1) | |
| 3. | Равными из векторов  , ,  и и  , где , где  , , 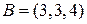 являются:
1) являются:
1)  2) 2)  3) 3)  4)все5)равных нет 4)все5)равных нет
| 5) | |
| 4. | Среди векторов  , ,  и и  коллинеарны:
1) коллинеарны:
1)  2) 2)  3) 3)  4)все5)нет коллинеарных 4)все5)нет коллинеарных
| 4) | |
| 5. | Из векторов  и и  коллинеарны вектору коллинеарны вектору  , где , где  , ,  :
1) :
1)  2) 2)  3) 3)  4) 4) 
| 1) | |
| Раздел: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. | |||
Тема 3.1. Прямая-1.
Прямая на плоскости (различные формы записи уравнения прямой на плоскости: проходящей через точку перпендикулярно вектору, параллельно вектору, через две точки, с угловым коэффициентом, в отрезках; угол между прямыми; точка пересечения прямых; расстояние от точки до прямой на плоскости; условия  и и  прямых). прямых).
| |||
| 1. | Даны вершины треугольника  : :  . Тогда уравнение медианы . Тогда уравнение медианы  , проведённой из вершины , проведённой из вершины  , имеет вид: , имеет вид:  , где , где  , ,  ( (  -целые числа).
Ответ записать в виде: -целые числа).
Ответ записать в виде: 
|  , , 
| |
Тема 3.3. Плоскость-1.
Тема 3.4. Плоскость-2.
Плоскость и прямая в пространстве (различные формы записи уравнения плоскости: проходящей через точку перпендикулярно вектору, через три точки, в отрезках; угол между плоскостями; расстояние от точки до плоскости; условия  и и  плоскостей; различные формы записи уравнения прямой в пространстве: проходящей через две точки, параметрическое; угол между прямыми, прямой и плоскостью; условия плоскостей; различные формы записи уравнения прямой в пространстве: проходящей через две точки, параметрическое; угол между прямыми, прямой и плоскостью; условия  и и  прямой и плоскости; точка пересечения прямой и плоскости). прямой и плоскости; точка пересечения прямой и плоскости).
| |||
| 1. | Плоскость  будет перпендикулярна прямой будет перпендикулярна прямой   при значении параметра при значении параметра  Записать ответ.
Записать ответ.
| 
| |
| 2. | Даны вершины пирамиды  : :  . Тогда расстояние от вершины . Тогда расстояние от вершины  до плоскости до плоскости  , проходящей через точку , проходящей через точку  перпендикулярно вектору перпендикулярно вектору  , равно , равно  , где , где  ( (  - целое число).
Ответ записать в виде: - целое число).
Ответ записать в виде: 
| 
| |
| Тема 3.5. Кривая-1. Классификация кривых второго порядка. Нахождение вершины параболы, центра и радиуса окружности, центров эллипса и гиперболы. | |||
| 1. | Уравнение  определяет:
1)эллипс 2) гиперболу 3) параболу определяет:
1)эллипс 2) гиперболу 3) параболу
| 3) | |
| 2. | Уравнение  определяет…..
1)окружность 2)эллипс 3)гиперболу5)параболу определяет…..
1)окружность 2)эллипс 3)гиперболу5)параболу
| 1) | |
| 3. | Точка  является центром эллипса является центром эллипса 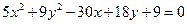 . Тогда координаты . Тогда координаты  точки точки  равны…
Ответ записать в виде: равны…
Ответ записать в виде: 
| 3,-1 | |
| 4. | Точка  является вершиной параболы является вершиной параболы  . Тогда координаты . Тогда координаты  точки точки  равны…
Ответ записать в виде: равны…
Ответ записать в виде: 
| 1,3 | |
| Тема 3.8. Геометрия (теория-2). Теоретические вопросы (в объёме вопросов к экзамену), в том числе: различные формы записи уравнений прямой и плоскости; взаимное расположение прямых и плоскостей (параллельность, перпендикулярность, пересечение, совпадение); нормальные уравнения сферы и окружности; расстояние от точки до прямой на плоскости; расстояние от точки до плоскости. | |||
| Раздел: ВВЕДЕНИЕ В АНАЛИЗ. | |||
| Тема 5.1: Функция-1:Область определения, элементы поведения основных элементарных функций (чётность и нечётность, периодичность, монотонность, ограниченность) . | |||
| 1. | Областью определения функции  является множество:
1) является множество:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 4) | |
| 2. | Областью определения функции  является отрезок является отрезок  , где , где  , ,  Ответ записать в виде:
Ответ записать в виде: 
| 
| |
| 3. | Какие из утверждений для функции  на промежутке на промежутке  являются верными:
1)периодическая2)немонотонная 3)неограниченная4)нечётная
В ответе указать все верные утверждения. являются верными:
1)периодическая2)немонотонная 3)неограниченная4)нечётная
В ответе указать все верные утверждения.
| 1)2)4) | |
| Тема 5.2: Функция-2:Область определения, множество значений, чётность (нечётность). | |||
| 1. | Даны функции А:  и В: и В:  .Нечётными из них (в области их определения) являются:
1) только А 2) только В 3) А и В 4) ни А, ни В .Нечётными из них (в области их определения) являются:
1) только А 2) только В 3) А и В 4) ни А, ни В
| 4) | |
| 2. | Функция  отображает множество отображает множество  на множество:
1) на множество:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 2) | |
Тема 5.3: Пределы-1.Пределы рациональных выражений  . .
| |||
| 1. | Предел  равен:
1) равен:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 4) | |
| 2. | Если  , то значение параметра , то значение параметра 
| 
| |
| 3. | Предел  равен:
1) равен:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 4) | |
| 4. | Предел  , где , где  ( (  -целое число)
Ответ записать в виде: -целое число)
Ответ записать в виде: 
| 
| |
| Тема 5.4: Пределы-2.Пределы иррациональных выражений. Пределы степенно-показательных функций. Пределы тригонометрических выражений. | |||
| 1. | Предел  равен:
1) равен:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 5) | |
| 2. | Предел  , где , где  ( (  - целое число)
Ответ записать в виде: - целое число)
Ответ записать в виде: 
| ||
| 3. | Предел  , где , где  ( (  - целое число)
Ответ записать в виде: - целое число)
Ответ записать в виде: 
| ||
| 4. | Предел  , где , где  ( (  - целое число)
Ответ записать в виде: - целое число)
Ответ записать в виде: 
| ||
| Тема 5.6: Непрерывность. | |||
| 1. | Даны функции
A:  и В: и В:  .
Непрерывнымииз них в точке .
Непрерывнымииз них в точке  являются:
1) только А 2) только В 3) А и В 4) ни А, ни В являются:
1) только А 2) только В 3) А и В 4) ни А, ни В
| 3) | |
| 2. | Дана функция . Точками её разрыва из перечисленных ниже точек являются:
1) . Точками её разрыва из перечисленных ниже точек являются:
1)  2) 2)  3) 3)  4) 4)  5) 5)  В ответе указать все точки разрыва функции.
В ответе указать все точки разрыва функции.
| 3)4) | |
| 3. | Функция  будет непрерывной в точке будет непрерывной в точке  при значении параметра при значении параметра  ( (  -целое число).
Ответ записать в виде: -целое число).
Ответ записать в виде: 
| ||
| 4. | Точка  является точкой бесконечного разрыва следующих из перечисленных ниже функций:
1) является точкой бесконечного разрыва следующих из перечисленных ниже функций:
1)  2) 2)  3) 3)  4) 4)  В ответе указать все функции, для которых
В ответе указать все функции, для которых  - точка бесконечного разрыва. - точка бесконечного разрыва.
| 1)2)4) | |
| Тема 5.7: Введение в анализ (теория). Теоретические вопросы (в объёме вопросов к экзамену), в том числе: бесконечно малые и большие функции, их свойства; свойства функций, имеющих конечный предел; сходимость ограниченных и монотонных числовых последовательностей; неопределённые выражения; непрерывность функции в точке; точки разрыва функции; свойства функций непрерывных на отрезке. | |||
10.
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов).
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным.
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
Конденсатор — это элемент электрической цепи, состоящий из проводящих электродов (обкладок), разделенных диэлектриком и предназначенный для использования его емкости.
КЛАССИФИКАЦИЯ КОНДЕНСАТОРОВ
В зависимости от назначения конденсаторы разделяются на две большие группы: общего и специального назначения.
Группа общего назначения включает в себя широко применяемые конденсаторы, используемые практически в большинстве видов и классов аппаратуры. Традиционно к ней относят наиболее распространенные низковольтные конденсаторы, к которым не предъявляются особые требования.
Все остальные конденсаторы являются специальными. К ним относятся: высоковольтные, импульсные, помехоподавляющие, дозиметрические, пусковые и др.
По характеру изменения емкости различают конденсаторы постоянной емкости, переменной емкости и подстроечные. Из названия конденсаторов постоянной емкости вытекает, что их емкость является фиксированной и в процессе эксплуатации не регулируется.
По характеру изменения емкости: - постоянные; переменные; подстроечные.
По способу защиты: - незащищенные; защищенные; неизолированные; изолированные; уплотненные; герметизированные.
По назначению: - общего назначения; специального.
11.
Диэлектрик (изолятор) — вещество, практически не проводящее электрический ток. Концентрация свободных носителей заряда в диэлектрике не превышает 108 см−3. Основное свойство диэлектрика состоит в способности поляризоваться во внешнем электрическом поле.
Электрическое поле в диэлектрике.
Рассмотрим плоский однородный диэлектрический слой, расположенный между двумя разноименно заряженными плоскостями. Пусть напряженность электрического поля, которое создается этими плоскостями в вакууме, равна ,
где - поверхностная плотность зарядов на пластинах (эти заряды называют свободными). Под действием поля диэлектрик поляризуется, и на его гранях появляются поляризационные или связанные заряды. Эти заряды создают в диэлектрике электрическое поле , которое направлено против внешнего поля .
,
где - поверхностная плотность связанных зарядов. Результирующее поле внутри диэлектрика
.
Поверхностная плотность связанных зарядов меньше плотности свободных зарядов, и не все поле E0 компенсируется полем диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая часть обрывается на связанных зарядах. Вне диэлектрика . Следовательно, в результате поляризации поле внутри диэлектрика оказывается слабее, чем внешнее . Таким образом,
,
где - диэлектрическая проницаемость среды. Из формулы видно, что диэлектрическая проницаемость показывает, во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике. Для вакуума , для диэлектриков .
13.
Условия на границе раздела двух диэлектриков.
Граничные условия для нормальных составляющих векторов D и E следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к границе раздела, а основания находятся на равном расстоянии от границы (рис. 2.6).
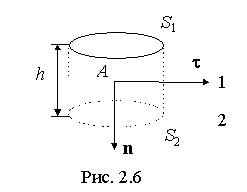
Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность
 .
.
Выделяя потоки через основания и боковую поверхность цилиндра
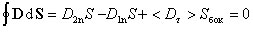 ,
,
где  - значение
- значение  касательной составляющей усредненное по боковой поверхности
касательной составляющей усредненное по боковой поверхности 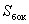 . Переходя к пределу при
. Переходя к пределу при 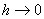 (при
(при 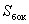 этом также стремится к нулю), получаем
этом также стремится к нулю), получаем  , или окончательно для нормальных составляющих вектора электрической индукции
, или окончательно для нормальных составляющих вектора электрической индукции
 .
.
Для нормальных составляющих вектора напряженности поля получим
 .
.
Таким образом, при переходе через границу раздела диэлектрических сред нормальная составляющая вектора 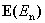 терпит разрыв, а нормальная составляющая вектора
терпит разрыв, а нормальная составляющая вектора  непрерывна.
непрерывна.
Граничные условия для касательных составляющих векторов D и E следуют из соотношения, описывающего циркуляцию вектора напряженности электрического поля. Построим вблизи границы раздела прямоугольный замкнутый контур длины lи высоты h (рис. 2.7).

Учитывая, что для электростатического поля
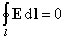 ,
,
и обходя контур по часовой стрелке, представим циркуляцию вектора E в следующем виде:
 ,
,
где 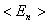 - среднее значение En на боковых сторонах прямоугольника. Переходя к пределу при
- среднее значение En на боковых сторонах прямоугольника. Переходя к пределу при 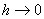 , получим для касательных составляющих E
, получим для касательных составляющих E
 .
.
Для касательных составляющих вектора электрической индукции граничное условие имеет вид
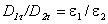
Таким образом, при переходе через границу раздела диэлектрических сред касательная составляющая вектора  непрерывна, а касательная составляющая вектора
непрерывна, а касательная составляющая вектора  терпит разрыв.
терпит разрыв.
Дата добавления: 2015-01-01; просмотров: 421; Мы поможем в написании вашей работы!; Нарушение авторских прав |