
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциелдық теңдеулер
$$$
Мына теңдеулердің қайсысы 1-ші ретті дифференциалдық теңдеу?
A) 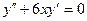
B) 
C) 
D) 
E) 
$$$
Мына теңдеулердің қайсысы 2-ші ретті дифференциалдық теңдеу?
A) 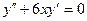
B) 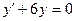
C) 
D) 
E) 
$$$
Мына теңдеулердің қайсысы 3-ші ретті дифференциалдық теңдеу?
A) 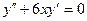
B) 
C) 
D) 
E) 
$$$
Төмендегі функциялардың қайсысы  теңдеуінің шешуі болады.
теңдеуінің шешуі болады.
A) 
B) 
C) y=3x
D) y=Sinx
E) y=Cosx
$$$
Төмендегі функциялардың қайсысы  теңдеуінің шешуі болады.
теңдеуінің шешуі болады.
A) 
B) 
C) y=3x
D) y=Sinx
E) y=-Cosx
$$$
Төмендегі функциялардың қайсысы  теңдеуінің шешуі болады.
теңдеуінің шешуі болады.
A) 
B) 
C) 
D) y=Sinx
E) y=-Cosx
$$$
Төмендегі функцияның қайсысы  теңдеуінің жалпы шешуі болады?
теңдеуінің жалпы шешуі болады?
A) y=Cx+3
B) 
C) 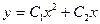
D) y=6x+C
E) 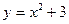
$$$
Төмендегі функцияның қайсысы  теңдеуінің жалпы шешуі болады?
теңдеуінің жалпы шешуі болады?
A) y=Cx+3
B) 
C) 
D) y=6x2+C
E) 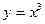
$$$
Төмендегі функцияның қайсысы  теңдеуінің жалпы шешуі болады?
теңдеуінің жалпы шешуі болады?
A) 
B) 
C) 
D) 
E) 
$$$
Төмендегі теңдеулердің қайсысы айнымалысы ажыратылған теңдеу болады?
A) xdx+y2dy=0
B) ydx+xdy=0
C) 5xdy+dx=0
D) M(x)dy+N(y)dx=0
E) 
$$$
Төмендегі теңдеулердің қайсысы айнымалысы ажыратылатын теңдеу болады?
A) xdx+y2dy=0
B) 
C) M(x)dx+N(y)dy=0
D) 
E) 
$$$
Төмендегі функциялардың қайсысы х пен у ке қарағанда 0-ші өлшемдес біртектес функция болады.
A) 
B) 
C) 
D) 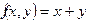
E) 
$$$
Төмендегі функциялардың қайсысы х пен у ке қарағанда 2-ші өлшемдес біртектес функция болады.
A) 
B) 
C) 
D) 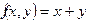
E) 
$$$
Төмендегі теңдеулердің қайсысы бірінші ретті біртектес теңдеу болады?
A) 
B) 
C) 
D) 
E) 
$$$
Төмендегі теңдеулердің қайсысы бірінші ретті біртектес теңдеу болады?
A) 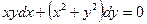
B) xydx+ydy=0
C) 5xdx+6xydy
D) (x+y)dx+y2dy=0
E) xdx+y3dy=0
$$$
Төмендегі теңдеулердің қайсысы бірінші ретті сызықтық теңдеу болады?
A) M(x)dx+N(y)dy=0
B) 
C) M(y)dx+N(x)dy=0
D) 
E) 
$$$
Төмендегі теңдеулердің қайсысы Бернулли теңдеуі болады?
A) M(x)dx+N(y)dy=0
B) 
C) M(y)dx+N(x)dy=0
D) 
E) 
$$$
xdx+ydy=0 дифференциалдық теңдеуін шешіңдер
A) x+y=C
B) xy=10
C) 
D) 
E) 
$$$
 теңдеуінің y(0)=1 алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
теңдеуінің y(0)=1 алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
A) x+y=C
B) 
C) xy=10
D) 
E) 
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) 
B) 
C) 
D) 
E) 
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) 
B) 
C) 
D) 
E) 
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) 
B) 
C) 
D) 
E) 
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) y=Cx-xlnx
B) y=Cx
C) y=Cx2-x2lnx
D) y=Cxlnx
E) y=x2+C
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) y=Cx
B) y=Cx+x2
C) y=Cx2
D) y=Cx+x3
E) y=Cx3
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) y=Cx
B) y=Cxlnx
C) y=x2+C
D) y=3xlnx+Cx
E) y=3lnx+C
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) y=Cx
B) y=Cx2
C) y=Cx+x3
D) 
E) 
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) y=Cx
B) 
C) 
D) y=Cx-x2
E) y=Cxlnx
$$$
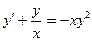 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) y(x2+Cx)=1
B) 
C) 
D) 
E) 
$$$
 теңдеуінің y(1)=1 алғашқы шартын қанағаттандыратын дербес шешуін тап
теңдеуінің y(1)=1 алғашқы шартын қанағаттандыратын дербес шешуін тап
A) 
B) 
C) 
D) 
E) 
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) 
B) 
C) 
D) 
D) 
$$$
Төмендегі теңдеулердің қайсысы толық дифференциалды теңдеу
A) 
B) 2xydx+x2dy=0
C) 2xydx+y2dy=0
D) xy2dx+x2dy=0
E) 5x2ydx+8xydy=0
$$$
(x+y)dx+(x+2y)dy=0 теңдеуінің жалпы шешуін тап
A) 
B) xy=10
C) y2=C
D) 
E) xy+y2=0
$$$
(x+y)dx+(x+2y)dy=0 теңдеуінің y(0)=1 алғашқы шартын қанағаттандыратын дербес шешуін тап
A) 
B) xy=2
C) y2=4
D) xy+y2=0
E) 
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) y=xlnx
B) y=-x+C1x
C) y=C1x+C2+xlnx-х
D) y=C1x+C2
E) y=C1+C2x
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) 
B) 
C) 
D) 
E) 
$$$
 теңдеуінің жалпы шешуін тап
теңдеуінің жалпы шешуін тап
A) 
B) 
C) 
D) y=C1+C2x
E) y=C1x+C2x2
$$$
Төмендегі теңдеулердің қайсысы 2-ші ретті сызықтық біртектес теңдеу болады
A) 
B) 
C) 
D) 
E) 
$$$
Төмендегі теңдеулердің қайсысы 2-ші ретті сызықтық біртектес емес теңдеу болады
A) 
B) 
C) 
D) 
E) 
$$$
Төмендегі теңдеулердің қайсысы сызықтық дифференциалдық теңдеу болады
A) 
B) 
C) 
D) 
E) 
$$$
Төмендегі теңдеулердің қайсысы сызықтық емес дифференциалдық теңдеу болады
A 
B 
C 
D 
E 
$$$
Коэффициенттері тұрақты 2-ші ретті сызықтық дифференциалдық теңдеуді тап
A 
B 
C 
D 
E 
$$$
 теңдеуінің сипаттаушы теңдеуін табыңдар
теңдеуінің сипаттаушы теңдеуін табыңдар
A 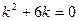
B 
C 
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің сипаттаушы теңдеуінің түбірлерін табыңдар
теңдеуінің сипаттаушы теңдеуінің түбірлерін табыңдар
A 
B 
C 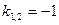
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 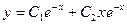
C 
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің дербес шешуін табыңдар
теңдеуінің дербес шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің дербес шешуін табыңдар
теңдеуінің дербес шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің
теңдеуінің  алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің
теңдеуінің  алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
A 
B 
C 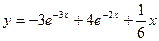
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің
теңдеуінің  алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің дербес шешуін табыңдар
теңдеуінің дербес шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің дербес шешуілерін табыңдар
теңдеуінің дербес шешуілерін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
$$$
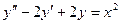 теңдеуінің дербес шешуін табыңдар
теңдеуінің дербес шешуін табыңдар
A 
B 
C 
D 
E 
$$$
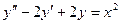 теңдеуінің
теңдеуінің  алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің сипаттаушы теңдеуін табыңдар
теңдеуінің сипаттаушы теңдеуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің
теңдеуінің  алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
алғашқы шартын қанағаттандыратын дербес шешуін табыңдар
A 
B 
C 
D 
E 
$$$
 теңдеуінің дербес шешуін табыңдар
теңдеуінің дербес шешуін табыңдар
A 
B 
C 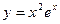
D 
E 
$$$
 теңдеуінің жалпы шешуін табыңдар
теңдеуінің жалпы шешуін табыңдар
A 
B 
C 
D 
E 
Дата добавления: 2015-01-05; просмотров: 452; Мы поможем в написании вашей работы!; Нарушение авторских прав |