
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введение. В задачах 101–120найти пределы функций, не пользуясь правилом Лопиталя.
В задачах 101–120найти пределы функций, не пользуясь правилом Лопиталя.
101.а) 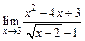 ; б)
; б) 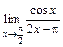 ; в)
; в) 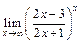 .
.
102.а)  ; б)
; б)  ; в)
; в)  .
.
103.а) 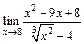 ; б)
; б)  ; в)
; в)  .
.
104.а) 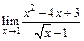 ; б)
; б)  ; в)
; в) 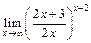 .
.
105.а)  ; б)
; б) 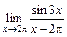 ; в)
; в) 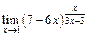 .
.
106.а)  ; б)
; б)  ; в)
; в)  .
.
107.а)  ; б)
; б) 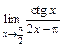 ; в)
; в) 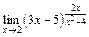 .
.
108.а)  ; б)
; б) 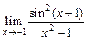 ; в)
; в)  .
.
109.а) 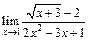 ; б)
; б)  ; в)
; в) 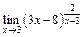 .
.
110.а)  ; б)
; б)  ; в)
; в)  .
.
111.а)  ; б)
; б) 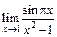 ; в)
; в)  .
.
112.а) 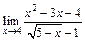 ; б)
; б)  ; в)
; в) 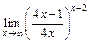 .
.
113.а)  ; б)
; б) 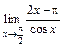 ; в)
; в)  .
.
114.а) 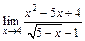 ; б)
; б)  ; в)
; в) 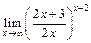 .
.
115.а) 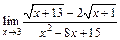 ; б)
; б)  ; в)
; в)  .
.
116.а)  ; б)
; б)  ; в)
; в)  .
.
117.а)  ; б)
; б) 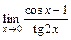 ; в)
; в)  .
.
118.а) 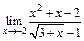 ; б)
; б)  ; в)
; в)  .
.
119.а)  ; б)
; б) 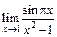 ; в)
; в)  .
.
120.а)  ; б)
; б)  ; в)
; в) 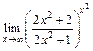 .
.
В задачах 121–140найти производные у'х.
121.а)  ;
;
б) 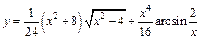 ,
,  ;
;
в)  ;
;
г)  ;
;
д) 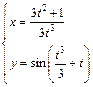 ;
;
122.а)  ;
;
б) 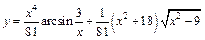 ,
,  ;
;
в)  ;
;
г)  ;
;
д) 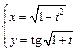 .
.
123.а)  ;
;
б) 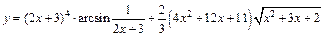 ,
,  ;
;
в) 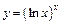 ;
;
г) 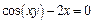 ;
;
д)  .
.
124.а) 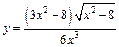 ;
;
б) 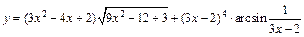 ,
, 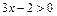 ;
;
в) 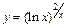 ;
;
г)  ;
;
д)  .
.
125.а)  ;
;
б)  ;
;
в) 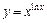 ;
;
г)  ;
;
д)  .
.
126.а) 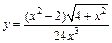 ;
;
б) 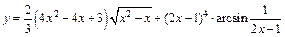 ,
,  ;
;
в)  ; г)
; г)  ; д)
; д) 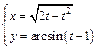 .
.
127.а)  ;
;
б)  ;
;
в) 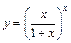 ;
;
г) 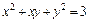 ;
;
д) 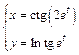 .
.
128.а)  ;
;
б)  ,
,  ;
;
в) 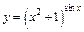 ;
;
г) 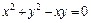 ;
;
д)  .
.
129.а) 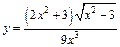 ;
;
б)  ;
;
в) 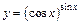 ;
;
г)  ;
;
д)  .
.
130.а) 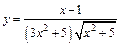 ;
;
б)  ,
,  ;
;
в) 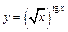 ;
;
г)  ;
;
д) 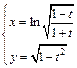 .
.
131.а) 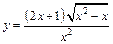 ;
;
б)  ,
, 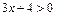 ;
;
в) 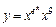 ;
;
г)  ;
;
д) 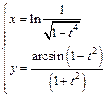 .
.
132.а)  ;
;
б) 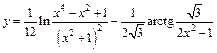 ;
;
в) 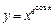 ;
;
г) 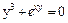 ;
;
д) 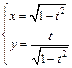 .
.
133.а) 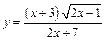 ;
;
б) 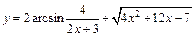 ,
,  ;
;
в)  ;
;
г) 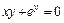 ;
;
д)  .
.
134.а)  ;
;
б)  ,
,  ;
;
в) 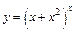 ;
;
г) 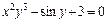 ;
;
д) 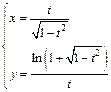 .
.
135.а)  ;
;
б) 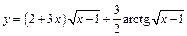 ;
;
в) 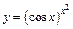 ;
;
г)  ;
;
д)  .
.
136.а) 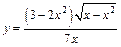 ;
;
б)  ;
;
в)  ;
;
г) 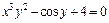 ;
;
д) 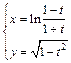 .
.
137.а) 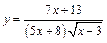 ;
;
б)  ;
;
в) 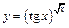 ;
;
г) 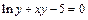 ;
;
д) 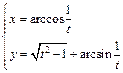 .
.
138.а)  ;
;
б) 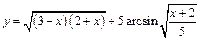 ;
;
в)  ;
;
г) 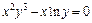 ;
;
д)  .
.
139.а) 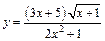 ;
;
б)  ,
,  ;
;
в)  ;
;
г) 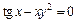 ;
;
д) 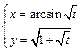 .
.
140.а)  ;
;
б)  ;
;
в) 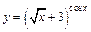 ;
;
г) 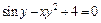 ;
;
д) 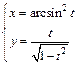 .
.
В задачах 141–160найти приближённое значение указанных величин с помощью дифференциалов соответствующих функций.
141.  . .
| 142.  . .
| 143.  . .
| 144.  . .
|
145.  . .
| 146. 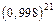 . .
| 147.  . .
| 148.  . .
|
149. 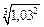 . .
| 150.  . .
| 151. 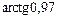 . .
| 152. 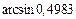 . .
|
153.  . .
| 154.  . .
| 155. 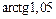 . .
| 156. 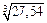 . .
|
157. 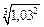 . .
| 158. 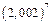 . .
| 159.  . .
| 160. 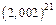 . .
|
В задачах 161–180исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проверить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция чётной, нечётной; 4) найти интервалы возрастания и убывания функции и точки её экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции.
161. 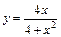 . .
| 162. 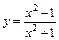 . .
|
163.  . .
| 164.  . .
|
165.  . .
| 166. 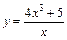 . .
|
167. 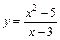 . .
| 168. 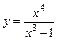 . .
|
169.  . .
| 170. 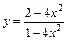 . .
|
171. 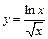 . .
| 172. 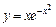 . .
|
173.  . .
| 174.  . .
|
175.  . .
| 176.  . .
|
177. 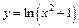 . .
| 178.  . .
|
179. 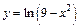 . .
| 180. 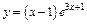 . .
|
181.Число 8 разбить на два таких слагаемых, чтобы сумма их кубов была наименьшей.
182.Какое положительное число, будучи сложено с обратным ему числом, даёт наименьшую сумму?
183.Число 36 разложить на два таких множителя, чтобы сумма их квадратов была наименьшей.
184.Требуется изготовить ящик с крышкой, объём которого был бы равен 72 см3, причём стороны основания относились бы, как 1:2. Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?
185.Из углов квадратного листа картона размером 18×18 см2 нужно вырезать одинаковые квадраты так, чтобы согнув лист по пунктирным линиям (см. рис.), получить коробку наибольшей вместимости. Какова должна быть сторона вырезаемого квадрата?
186.Решить предыдущую задачу для прямоугольного листа размером 8×5 см2.
187.Объём правильной треугольной призмы равен V. Какова должна быть сторона основания, чтобы полная поверхность призмы была наименьшей?
188.Открытый чан имеет форму цилиндра. При данном объёме V каковы должны быть радиус основания и высота цилиндра, чтобы его поверхность была наименьшей?
189.Найти соотношение между радиусом R и высотой Н цилиндра, имеющего при данном объёме V наименьшую полную поверхность.
190.Требуется изготовить коническую воронку с образующей, равной 20 см. Какова должна быть высота воронки, чтобы её объём был наибольшим?
191.Из круга вырезан сектор с центральным углом α. Из сектора свёрнута коническая поверхность. При каком значении угла α объём полученного конуса будет наибольшим?
192.Периметр равнобедренного треугольника равен 2р. Каковы должны быть его стороны, чтобы объём тела, образованного вращением этого треугольника вокруг его основания, был наибольшим?
193.Периметр равнобедренного треугольника равен 2р.Каковы должны быть его стороны, чтобы объём конуса, образованного вращением этого треугольника вокруг высоты, опущенной на основание, был наибольшим?
194.Найти высоту цилиндра наибольшего объёма, который можно вписать в шар радиуса R.
195.Найти высоту конуса наибольшего объёма, который можно вписать в шар радиуса R.
196.Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R.
197.Каков должен быть угол при вершине равнобедренного треугольника заданной площади, чтобы радиус вписанного в этот треугольник круга был наибольшим?
198.Доказать что конический шатёр данной вместимости требует наименьшего количества материи, когда его высота в 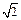 раз больше радиуса основания.
раз больше радиуса основания.
199.Найти наименьший по площади эллипс, описанный около данного прямоугольника (площадь эллипса с полуосями а и b равна πab).
200.Полоса железа шириной а должна быть согнута в виде открытого цилиндрического желоба (сечение желоба имеет форму дуги кругового сегмента). Найти значение центрального угла, опирающегося на эту дугу, при котором вместимость желоба будет наибольшей.
В задачах 201–220найти неопределённые интегралы.
201.а) 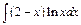 ; б)
; б) 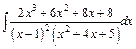 ; в)
; в)  .
.
202.а) 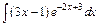 ; б)
; б)  ; в)
; в) 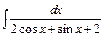 .
.
203.а) 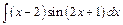 ; б)
; б)  ; в)
; в)  .
.
204.а) 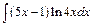 ; б)
; б) 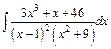 ; в)
; в) 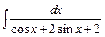 .
.
205.а) 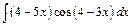 ; б)
; б)  ; в)
; в)  .
.
206.а) 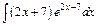 ; б)
; б)  ; в)
; в) 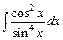 .
.
207.а)  ; б)
; б)  ; в)
; в)  .
.
208.а) 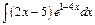 ; б)
; б)  ; в)
; в)  .
.
209.а)  ; б)
; б) 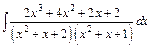 ; в)
; в) 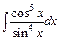 .
.
210.а)  ; б)
; б)  ; в)
; в)  .
.
211.а)  ; б)
; б) 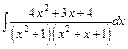 ; в)
; в)  .
.
212.а) 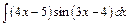 ; б)
; б) 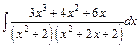 ; в)
; в)  .
.
213.а)  ; б)
; б) 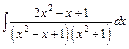 ; в)
; в) 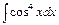 .
.
214.а)  ; б)
; б) 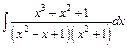 ; в)
; в) 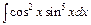 .
.
215.а)  ; б)
; б)  ; в)
; в) 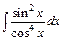 .
.
216.а) 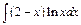 ; б)
; б) 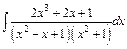 ; в)
; в)  .
.
217.а) 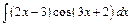 ; б)
; б)  ; в)
; в) 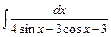 .
.
218.а) 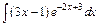 ; б)
; б)  ; в)
; в) 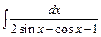 .
.
219.а) 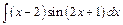 ; б)
; б)  ; в)
; в) 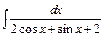 .
.
220.а)  ; б)
; б)  ; в)
; в) 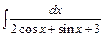 .
.
В задачах 221–240вычислить несобственный интеграл или доказать его расходимость.
221. 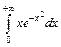 . .
| 222. 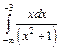 . .
| 223.  . .
|
224.  . .
| 225.  . .
| 226. 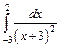 . .
|
227.  . .
| 228.  . .
| 229. 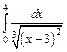 . .
|
230.  . .
| 231. 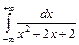 . .
| 232.  . .
|
233. 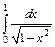 . .
| 234.  . .
| 235. 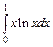 . .
|
236.  . .
| 237. 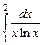 . .
| 238. 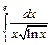 . .
|
239. 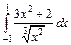 . .
| 240. 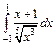 . .
|
В задачах 241–243вычислить площади фигур, ограниченных графиками функций.
241.  , , 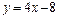 . .
| 242. 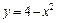 , ,  . .
|
243.  , ,  . .
|
В задачах 244–246вычислить площади фигур, ограниченных линиями, заданными параметрически.
244. 
| 245. 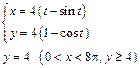
|
246. 
|
В задачах 247–250вычислить площади фигур, ограниченных линиями, заданными уравнениями в полярных координатах.
247. 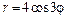 , ,  . .
| 248. 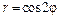 . .
|
249.  , , 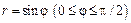 . .
| 250. 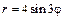 , , 
|
В задачах 251–253вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
251. 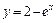 ,
,  .
.
252.  ,
, 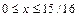 .
.
253. 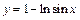 ,
,  .
.
В задачах 254–256вычислить объёмы тел, образованных вращением вокруг оси Ох фигур, ограниченных графиками функций.
254. 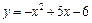 ,
, 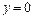 .
.
255.  ,
, 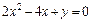 .
.
256.  ,
, 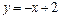 ,
, 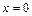 .
.
В задачах 257–260вычислить объёмы тел, образованных вращением вокруг оси Оу фигур, ограниченных графиками функций.
257.  ,
, 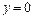 ,
, 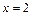 .
.
258.  ,
,  .
.
259.  ,
, 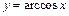 ,
, 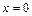 .
.
260.  ,
, 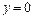 ,
, 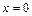 ,
, 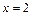 .
.
КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ
для специальностей 311300, 030500
Составители: Шефель Валентина Гавриловна
Грунина Мария Викторовна
Бабин Владислав Николаевич
Редактор В.В. Попова
Лицензия № 020426 от 7 мая 1997 г.
Подписано к печати 1.04.1999 г.
Формат 84×108 1/32
Объем 1,7 уч.–изд. л.
Тираж 600 экз.
Отпечатано в ИЗОП
630039, Новосибирск, ул. Никитина, 155
Введение
Конституция РФ гарантирует:
статья 37. «…Каждый имеет право на труд в условиях, отвечающих требованиям безопасности и гигиены…» требует от нас обеспечить безопасность и гигиену труда.
На основании этого разработано много документов и подзаконных актов, которые направлены на сохранение здоровья и работоспособности.
Важным моментом в комплексе мероприятий направленных на совершенствование условий труда являются мероприятия по безопасности жизнедеятельности. Этим вопросам с каждым годом уделяется все большее внимание, т.к. забота о здоровье человека стала не только делом государственной важности, но и элементом конкуренции работодателей в вопросе привлечения кадров.
Обеспечение нормальных (комфортных) условий деятельности людей, улучшение условий труда и повышение его безопасности приводят к снижению производственного травматизма, уменьшению случаев профессиональных заболеваний, инвалидности, что не только сохраняет здоровье работников, но и снижает затраты на оплату льгот и компенсаций за работу в неблагоприятных условиях труда.
Целью данного раздела дипломного проекта является анализ безопасности оператора, работающего на токарно-фрезерном станке с ЧПУ PowerTurn – 1600, а именно:
1. Анализ наиболее опасных и вредных производственных факторов, влияющих на оператора токарно -фрезерного станка с ЧПУ PowerTurn – 1600 на его рабочем месте, определения их источника и степени влияния на работающиго.
2. Оценка безопасности основных источников опасности, действующих на работающего.
3. Оценка безопасности рабочего места и по существующим СКЗ и СИЗ снизить воздействие параметров источника опасности для предельно допустимых значений.
4. Разработка мероприятий по молниезащите цеха
Дата добавления: 2015-01-05; просмотров: 501; Мы поможем в написании вашей работы!; Нарушение авторских прав |