КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА 18. ОСНОВЫ ТЕРМОДИНАМИКИ
18.1 Внутренняя энергия и работа идеального газа. Первый закон термодинамики и его применение к изопроцессам
| Внутренняя энергия идеального газа: U = νiRT/2 = miRT/2M = ipV/2, где ν – количество вещества, m - масса газа; M – молярная масса газа; p, V -давление и объем; i - число степеней свободы; R – универсальная газовая постоянная. Изменение внутренней энергии идеального газа: dU = miRdT/2M |
Элементарная работа, совершаемая газом при изменении его объема:
∂A = pdV = mRdT/M.
Полная работа при изменении объема газа: A =  .
Изобарный процесс: A = p(V2-V1) = mR(T2 –T1)/M .
Изотермический процесс:
A = mRT(ln V2/V1)/M = mRT(ln p1/p2)/M = p1V1ln(V2/V1) = p2V2·ln(p1/p2)
Изохорический процесс: A = 0
|
| Первый закон термодинамики; Q = ΔU + A, где Q – количество теплоты, сообщенное системе или отданное ею; ΔU - изменение внутренней энергии; A –работа системы против внешних сил V = const Q = ΔU; T = const Q = A; p = const Q = ΔU + A |
18.2 Теплоемкость идеального газа
| Теплоемкость тела: C =∂Q/dT, гдe ∂Q -количество подведенной теплоты; dT - приращение температуры |
| Mолярная теплоемкость тела: Cμ= C/M = ∂Q/MdT, где M - молярная масса |
| Удельная теплоемкость: c = C/m = ∂Q/mdT где m - масса тела |
| Молярная изохорная теплоемкость газа: Cv = iR/2, где i – число степеней свободы молекул; R – универсальная газовая постоянная. Удельная изохорная теплоемкость газа: cv = Cv/M = iR/2M |
| Молярная изобарная теплоемкость газа: CP = (i+2)R/2; Удельная изобарная теплоемкость газа: cP = CP/M = (i +2)R/2M |
| Уравнение Майера: CP – CV = R; сP – сV = R/μ. |
| Показатель адиабаты (отношение теплоемкостей при постоянных давлении и объеме): CP/Cv = (i +2)/i |
18.3 Адиабатический процесс. Уравнение Пуассона
| Первый закон термодинамики для адиабатного процесса: Q =0; A + ΔU =0; A = - ΔU |
| Уравнение Пуассона: pVγ = const; TVγ-1 = const; Tγp1-γ = const, где γ = CP/Cv |
| Работа газа при адиабатном процессе: A = -ΔU = mcv (T1 –T2); A = RT1m [1 – (V1/V2)γ-1]/(γ – 1)M = p1V1[1 – (V1/V2)γ-1]/(γ–1), где T1, T2, V1, V2 - соответственно начальные и конечные значения температуры и объемов газа |
18.4 Тепловые двигатели. Цикл Карно и его КПД
| Термический коэффициент полезного действия для кругового процесса (цикла): η = A/Q1 = (Q1 – Q2)/Q1 = 1 – Q2/Q1, где Q1 – количество теплоты, полученное системой; Q2 – количество теплоты, отданное системой; A – работа, совершаемая за цикл |
| Термический коэффициент полезного действия цикла Карно: η = (T1 – T2)/T1 = 1 – T2/T1, где T1 и T2 - соответственно термодинамические температуры нагревателя (теплоотдатчика) и холодильника (теплоприемника) |
18.4 Второй закон термодинамики. Неравенство Клаузиуса. Энтропия
Неравенство Клаузиуса: 
|
| Полный дифференциал энтропии: dS = δQ/T Дифференциал энтропии идеального газа: dS = (CvdT/T + RdV/V)m/M; dS = (CPdT/T – Rdp/p)m/M; dS = (CPdV/V + Cvdp/p)m/M. |
Изменение энтропии при равновесном переходе из состояния 1 в состояние 2: ∆S12 = S2 – S1 =  =  .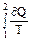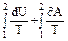
Изменение энтропии в процессах идеального газа:
p = const S12 = S2 –S1 = (Cvln T2/T1 +RlnV2/V1)m/M;
T = const S = ( mRlnV2/V1)/M = (mRlnp2/p1)/M
V = const S = (mCvlnT2/T1)/M = (mCVln p2/p1)/M
Q = 0 S = const
|
Изменение энтропии системы: ΔS =  ,
где ∆Si - изменение энтропии i–й компоненты
|
Формула Больцмана для энтропии:  S
w – термодинамическая вероятность;
S – энтропия;
k – nостоянная Больцмана
|
| Втoрой закон термодинамики: dS > 0; ∂Q < TdS; TdS < dU + ∂A, где dU - изменение энергии системы; ∂A – работа, совершаемая над системой; dS - изменение энтропии системы. |
Пример 24.Двухатомный идеальный газ занимает при давлении р1 = 3·105 Па объем V1 = 4 л, его расширяют до объема V2 = 6 л, при этом давление падает до значения р2=1,0·105 Па. Процесс происходит сначала по адиабате, затем по изохоре. Определить работу сил давления газа А, изменение внутренней энергии и количество теплоты Q, поглощенной при переходе.
Условие:
р1 = 3,0∙105 Па;
р2 = 1,0∙105 па;
V1 = 4 л = 4,0∙10-3 м3;
V2 = 6 л = 6,0∙10-3 м3;
А - ? U -? Q - ?
Решение. Газ участвует в двух процессах: а) адиабатное расширение из состояния 1 в состояние 2, при котором объем V2, давление р – неизвестно; б) изохорный переход из состояния 2 в состояние 3. Чтобы определить характер изохорного процесса – нагревание или охлаждение – надо найти промежуточное значение давления р.
Согласно уравнению адиабаты р2/р1 = (V1/V2)γ (1)
Газ двухатомный, следовательно, γ=(i + 2)/i =1,4.
Таким образом р = 3,105 (2/3)1,4 > р2 = 1,0·105 Па.
Последнее неравенство показывает, что при изохорном переходе из состояния 2 в состояние 3 давление газа уменьшается и, следовательно, процесс 2-3 есть процесс изохорного охлаждения (р/Т = соnst при V =const).
Чтобы найти работу А12 и количество поглощенной теплоты Q13 при переходе из состояния 1 в состояние 3 надо рассмотреть каждый из указанных процессов отдельно. При этом
А13 = А12 + А23, Q13 = Q12 + Q23.
Изменение внутренней энергии не зависит от процесса и в любом случае
U = i m R(T2 – T1)/2M. (31)
Неизвестные значения Т1 и Т2 и m/M можно найти из уравнения Клапейрона - Менделеева. На участке 1- 2 количество поглощенной теплоты Q12 = 0. Работа газа А12 может быть определена по изменению внутренней энергии U12 с использованием уравнения Клапейрона – Менделеева и уравнения адиабаты. На участке 2-3 работа газа А23 = 0, количество поглощенной теплоты
Q23 = m Cv(T2 – T1)/M. (2)
Работа газа при адиабатном процессе
А12 = - U12 = i m R(T2 – T1)/2M.
Используя уравнение Клапейрона – Менделеева для состояний 1 и 2 получим
А12 = i (p1V1 – p2V2)/2.
Из уравнения адиабаты
р = р1 (V1/ V2)γ = 1,7·105 Па.
Тогда А12 = 450 Дж. Учитывая, что А23 = 0, находим А12 = А13 = 450 Дж.
При изохорном процессе молярная теплоемкость Сv = iR/2. Подставляя это выражение в уравнение (32) и используя уравнение Клапейрона – Менделеева для состояний 2 и 3, получим
Q23 = i ( p2 V2 – p V2 ) = - 1050 Дж.
Поскольку Q12 = 0, общее количество теплоты Q13 = Q23 = = - 1050 Дж. Знак минус показывает, что газ отдавал теплоту окружающим телам. Изменение внутренней энергии согласно (3)
U12 = i ( p2 V2 – p1 V1)/2 = - 1050 Дж.
Пример 25.Кислород, масса которого m = 200 г нагревают от температуры t1 =270 С до t2 = 1270 С. Найти изменение энтропии, если известно, что начальное и конечное давления одинаковы и близки к атмосферному.
Условие:
m = 200 г = 0,200 кг;
Т1 = 270 С = 300 К;
Т2 = 1270 С = 400 К;
i = 5;
M = 32·10-3 кг/моль;
Δ S - ?
Решение. Газ подчиняется законам идеального газа, характер процесса нагрева неизвестен, но изменение энтропии системы при переходе из одного состояния в другое определяется только параметрами состояния и не зависит от характера процесса.
Найти изменение энтропии можно, рассмотрев произвольный обратимый процесс, в результате которого систему (в данном случае идеальный газ) можно перевести из состояния 1 в состояние 2 (рис.8).
На рис. 8 показаны два возможных квазистатических процесса: первый – изобарное расширение 1 –2; второй – изотермическое расширение 1 – 3 с последующим изохорным нагреванием 3- 2.
Для процесса 1 –2 S2 - S1 = 
(1)
где Qp = m Cp dT/M.
Для процесса 1-3-2 S2 - S1 =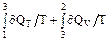 
, (2)
где ∂QT = ∂A = pdV, ∂QV = mCVdT/M.
Найдем изменение энтропии, рассматривая изобарный процесс 1-2. При изобарном процессе молярная теплоемкость СР = const = (i + 2)R/2. Подставляя выражение QP под знак интеграла равенства (33) и учитывая постоянство СР, получим
S2 - S1 = 
= m(i +2)R ln (T2/T1)/2M = 52 Дж/К.
Результат не изменится и при переходе 1-3-2. Подставляя выражения QT и QV в (34) и учитывая, что при изотермическом процессе р = р1 V1/V = mRT1/MV получим
S2 – S1 = mRln (V2/V1)/M + mCVln (T2/T1)/M.
Учитывая, что Т2 = Т1, V3 = V2, а также Т2/Т1 = V2/V!, получим
S2 – S1 = m(i + 2)R ln (T2/ T1)/2M = 52 Дж/К.
Дата добавления: 2014-10-31; просмотров: 147; Мы поможем в написании вашей работы!; Нарушение авторских прав |