РОССИЙСКАЯ ФЕДЕРАЦИЯ. § 15) Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

§ 15) Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

Теорема Томсона связывает период собственных электрических или электромагнитных колебаний в контуре с его ёмкостью и индуктивностью.^[1]

Формула Томсона выглядит следующим образом^[2]:

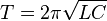
16) Всякий реальный контур обладает активным сопротивлением (рис. 4.3). Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего колебания затухают. Добро́тность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний ,

где:

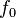· — резонансная частота колебаний

· — энергия, запасённая в колебательной системе

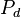· — рассеиваемая мощность.

Апериодический режим в R-L-C контуре наблюдается при большом затухании, когда . В этом случае корни P1,2 вещественные, отрицательные, различные.

17) Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями.

Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Внешний источник периодического воздействия обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

Частота вынужденных колебаний равна частоте вынуждающей силы. В случае, когда частота вынуждающей силы υ совпадает с собственной частотой колебательной системы υ₀, происходит рез­кое возрастание амплитуды вынужденных колебаний — резонанс. Резонанс возникает из-за того, что приυ = υ₀ внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает по­ложительную работу: энергия колеблющегося те­ла увеличивается, и амплитуда его колебаний становится большой. График зависимости амплитуды вынужденных колебаний А_т от частоты вынужда­ющей силы υ представлен на рисунке, этот график называется резонансной кривой:

18 сопротивление елекромагнитного колебательного контура : индуктивное емкостное реактивное активное полное

Если ЭДС в контуре задается соотношением ε = ε₀sin(ωt+φ), или при напряжении на концах участка цепи U=U₀sin(ωt+φ), то мгновенные значения силы тока в этом контуре (на этом участке цепи) I = I₀ sin ωt, т.е. существует сдвиг фаз между колебаниями напряжения и силы тока. Отношение амплитуды колебаний напряжения к амплитуде силы тока на каком-либо элементе цепи называется сопротивлением данного элемента переменному току. Сопротивление резистора переменному току (равно его омическому сопротивлению R) называется активным сопротивлением.Сопротивление конденсатора переменному X_C = 1/ωCназывается емкостным сопротивлением.Сопротивление катушки индуктивности переменному току X_L = ωLназывается индуктивным сопротивлением.Резонанс в электрической цепи наступает при приближении частоты вынужденных колебаний к частоте собственных колебаний контура, в результате чего наблюдается резкое возрастание амплитуды силы тока. При равенстве частот ω = ω₀ амплитуда силы тока I₀ достигает максимального значения . Одновременно с увеличением силы тока при резонансе возрастает амплитуда напряжения на конденсаторе и катушке индуктивности, которые могут стать существенно большей, чем амплитуда напряжениявнешнего источника U₀.

19) Ур. Максвела

20) Ур. Максвела

21)

Электромагнитная волна - процесс распространения электромагнитного поля в пространстве.

Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.

Волновое уравнение: Иными словами, уберём из этих уравнений все заряды и токи. Для однородной и изотропной среды, не обладающей ферромагнитными и сегнетоэлектрическими свойствами (такая среда называется линейной, поскольку выполняется линейная связь между напряженностью и индукцией электрического и магнитного полей соответственно), получим:

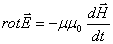
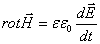
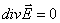
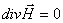
Путём чисто математических преобразований, без каких-либо дополнительных предположений эти уравнения приводятся к виду:

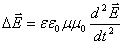
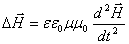
А это есть ни что иное, как волновые уравнения для векторов напряженности электрического и магнитного полей. Мы знаем, что коэффициент в правой части уравнений есть обратный квадрат фазовой скорости волны; отсюда сразу находим эту скорость:

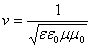
В вакууме e = m = 1, откуда получаем результат, весьма озадачивший современников Максвелла: скорость распространения электромагнитных волн в вакууме есть константа, не зависящая от системы отсчета (уравнения Максвелла, как известно, не инвариантны к преобразованиям Галилея):

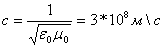
22) Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:

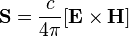(в системе СГС),

(в СИ),

где E и H — векторы напряжённости электрического и магнитного полей соответственно.

23) Корпускулярная и волновая теории света: Согласно корпускулярной теории (или теории истечения) свет представляет собой поток частиц (корпускул) , которые испускаются источником света. Эти частицы движутся в пространстве и взаимодействуют с веществом по законам механики.

Эта теория хорошо объясняла законы прямолинейного распространения света, его отражения и преломления. Основоположником данной теории является Ньютон.
Волнова́я тео́рия све́та — одна из теорий, объясняющих природу света. Основное положение теории заключается в том, что свет имеет волновую природу, то есть ведёт себя как электромагнитная волна, от длины которой зависит цвет видимого нами света.

Теория подтверждается многими опытами (в частности, опытом Т. Юнга), и данное поведение света (в виде электромагнитной волны) наблюдается в таких физических явлениях, как дисперсия, дифракция и интерференция света. Однако многие другие физические явления, связанные со светом, одной волновой теорией объяснить нельзя.

24) Теория отражения света:

25) Закон преломления света: Падающий и преломленный лучи и перпендикуляр, проведенный к границе раздела двух сред в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред:
,
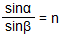где α — угол падения,
β — угол преломления,
n — постоянная величина, не зависящая от угла падения.

При изменении угла падения изменяется и угол преломления. Чем больше угол падения, тем больше угол преломления.
Если свет идет из среды оптически менее плотной в более плотную среду, то угол преломления всегда меньше угла падения: β < α.
Луч света, направленный перпендикулярно к границе раздела двух сред, проходит из одной среды в другую без преломления.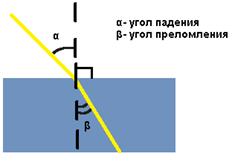

26)Принцип Гюйгенса является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка фронта(поверхности, достигнутой волной) является вторичным (т.е. новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.

Принцип ГюйгенсаКаждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

27) Из принципа Ферма (так его обычно называют) следует, что в однородной среде (в такой среде скорость света всюду одинакова) свет должен распространяться прямолинейно: прямая — кратчайшее расстояние между двумя точками, следовательно, и время распространения — наименьшее.

Покажем теперь, что закон отражения света — тоже прямое следствие принципа Ферма.

28) Суперпозиция волн: Принцип суперпозиции (наложения) волн заключается в следующем: в линейных средах волны распространяются независимо друг от друга, то есть волна не изменяет свойства среды, и другая волна распространяется так, будто первой волны нет. Это позволяет вычислять итоговую волну как сумму всех волн, распространяющихся в данной среде.

При сложении двух или более синусоидальных волн результирующая волна в общем случае уже не будет синусоидальной.

Рассмотрим в качестве примера результат сложения двух плоских однонаправленных волн с одинаковыми амплитудами и разными, но близкими частотами и волновыми числами:

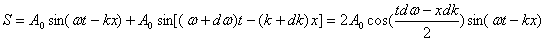
29) Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

Под когеpентностью понимается согласованность волн дpуг с дpугом по фазе. Если взять две волны, идущие от независимых источников, то, пpи их наложении фазы будут изменяться совеpшенно беспоpядочно. Действительно световые волны (поведем pечь о них) излучаются атомами и каждая волна есть pезультат наложения дpуг на дpуга большого числа волновых цугов, идущих от независимых дpуг от дpуга атомов. "Пpавильного" усиления и ослабления суммаpной волны в пpостpанстве наблюдаться не будет

30) Способы получения интерфенционных картин:

1.Разделение волны по фронту. Примером такого способа является классический опыт Юнга. Он был впервые осуществлен английским физиком Томасом Юнгом в 1807 году. В нем яркий пучок солнечного света освещал узкую щель S (рис.3.6.3). Прошедший через щель свет вследствие дифракции образует расходящуюся волну, которая падает на две узкие щели S1 и S2. Эти щели действуют как вторичные когерентные источники, и Рис.3.6.3.

исходящие из них дифрагированные волны, перекрываясь, дают на экране Э систему интерференционных полос. Проведя расчет как было показано выше, можно найти координаты максимумов и минимумов на экране и ширину интерференционных полос. Однако в опыте Юнга простая картина интерференции

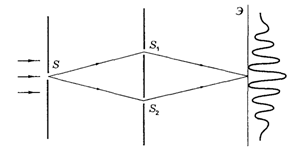
2.Разделение волны по амплитуде (по ходу волны). Примером такого способа является интерференция в тонких пленках. Пусть на прозрачную плоскопараллельную пластинку падает плоская монохроматическая световая волна, направление распространения которой показано падающим лучом на рис.3.6.5. В результате отражений от обеих поверхностей пластинки исходная волна расщепится на две, что и показано лучами 1 и 2. Амплитуды этих волн мало отличаются друг от друга — это важно для получения достаточно контрастной интерференции.

31) Рассмотрим интерференционную картину, полученную методом Юнга (рис. 8.2).

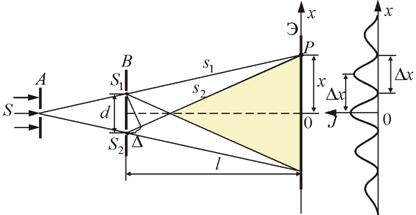
Рис. 8.2

Свет от источника S, прошедший через узкую щель в экране А, падет на экран В с двумя щелями S₁ и S₂, расположенными достаточно близко друг к другу на расстоянии d. Эти щели являются когерентными источниками света. Интерференция наблюдается в области, в которой перекрываются волны от этих источников (поле интерференции). На экране Э мы видим чередование полос с максимумом и минимумом интенсивности света.

Экран расположен на расстоянии l от щелей, причем .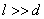

Рассмотрим две световые волны, исходящие из точечных источников S₁ и S₂. Показатель преломления среды – n.

Вычислим ширину полос интерференции (темных и светлых полос).

Интенсивность в произвольной точке P экрана, лежащей на расстоянии x от О, определяется (для вакуума, когда n = 1) оптической разностью хода .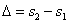

32) Интерференционные полосы равного наклона: ПОЛОСЫ РАВНОГО НАКЛОНА - чередующиеся тёмные и светлые полосы (интерференционные полосы), возникающие при падении света на плоскопараллельную пластину в результате интерференции лучей, отражённых от верхней и нижней её поверхностей и выходящих параллельно друг другу. Монохроматич. свет с длиной волны 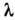от точечного источника S (рис.), находящегося в среде с показателем преломления п, падает на пластину толщиной h и с показателем преломления при отражении луча SA от верхней и нижней граней образуются параллельные лучи AD и СЕ. Оптич. разность хода между такими лучами

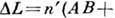
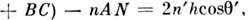а соответствующая разность фаз 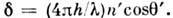С учётом сдвига фаз на

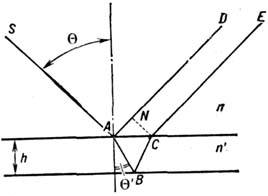
при отражении

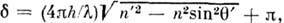
РОССИЙСКАЯ ФЕДЕРАЦИЯ