Возраст Фаза Луны и её видимость

Информатика и вычислительная техника, очная

нет отзывов

нет

—

112000 Р

Возраст Фаза Луны и её видимость

0 или 30 дней Новолуние. Луна не видна.

7 дней Первая четверть. Наилучшее время для наблюдений – вечер.

15 дней Полнолуние. Видна всю ночь от заката до восхода Солнца.

22 дня Последняя четверть. Луну лучше наблюдать во второй половине ночи, под утро.

Для вычисления возраста Луны воспользуемся формулой, выведенной автором:

W=L•11-14+D+M, где

W – возраст Луны (в сутках),

L – «лунное число», которое мы рассчитаем отдельно,

D – дата, на которую проводятся расчеты (например, для 14 марта D=14)

М – число, указывающее на номер календарного месяца (например, M=3 для марта и M=5 для мая),

«Лунное число» L зависит от года. Оно меняется от 1 до 19, а затем снова «обращается» в 1. В таблице 2 приводятся «лунные числа» для некоторых лет, однако, полностью запоминать её наизусть не следует. Не забудьте лишь, что в 2001 году (первом году XXI века) «лунное число» равнялось 7. Данные для остальных лет легко вычислить.

Таблица 2.

Год 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007

L 19 1 2 3 4 5 6 7 8 9 10 11 12 13

Кроме того, если при промежуточных вычислениях мы получили сумму большую, чем 30, то можно упростить себе жизнь, вычтя это число из результата… Надеюсь, сейчас вам всё станет ясно из конкретного примера!

Пример 1.

• Давайте рассчитаем возраст Луны (W), скажем, на 12 апреля 2005 года:
• А) Находим число L. Из таблицы 2 видно, что «лунное число» для 2005 года равно 11. Если бы таблицы 2 не было под рукой, то, помня, что в 2001 году L=7, можно без особых ухищрений получить значение L и для любого другого года, как в прошлом, так и в будущем. Помните, что c каждым годом L увеличивается на единицу, а после того, как достигнет 19, скачком «превращается» в 1. (Посмотрите в таблице 2 данные для 1994 и 1995 годов!)
• Б) Умножая L на 11, что просто сделать в уме, получаем 121. Вычитаем 14. Остается 107. Полученный результат явно превышает 30, поэтому вычитаем 30 несколько раз, пока, в конце концов, не получим 17. (107-30-30-30=17 или 107-3•30=17)
• В) Для 12 апреля D=12, M=4, Поэтому возраст Луны на этот день будет равен W=17+12+4=33. Результат снова больше 30, поэтому вычитаем 30 и в итоге получаем 3. Значит, 12 апреля 2005 года возраст Луны составит трое суток после новолуния, и её узкий серпик будет красоваться на фоне вечерней зари…

ФОРМУЛА ФАЗЫ

• Возраст же Луны отсчитывается обычно от новолуния. Элонгация будет
  L = (360° * t)/29.53 = 12.19° * t
  И формула для фазы в зависимости от элонгации будет
  Ф = (sin(L/2))^2
  Для полнолуния (t=15 дней) L=180°; Ф=1,0
  Для четверти (t=7 дней) L=90° Ф=0.50
  (t=22 дня) L=270 Ф=0.50
  
  
  Ф = фаза, лямбда - фазовый угол, t = возраст
• Во время новолуния Луна проходит между Солнцем и Землей (т. е. находится в соединении с Солнцем), фазовый угол чр = 180°, к Земле обращена темная сторона Луны и она не видна на небе. Дня через два после новолуния Луна видна в виде узкого серпа на западе, в лучах вечерней зари, вскоре после захода Солнца. Лунный серп, обращенный выпуклостью к Солнцу, ото дня ко дню постепенно расширяется и приблизительно через семь суток после новолуния принимает форму полукруга. Наступает фаза, называемая первой четвертью. В это время Луна находится в восточной квадратуре, т. е. на 90° к востоку от Солнца, фазовый угол яр = 90°, и к Земле обращена половина освещенного и половина неосвещенного полушария Луны. При этой фазе Луна вндна в первой половине ночи, а затем заходит за горизонт. С каждым днем с Земли видна все большая часть освещенного полушария Луны и приблизительно через семь суток после первой четверти наступает полнолуние, когда Луна имеет вид полного круга. Во время полнолуния Луна находится в противостоянии с Солнцем, г}> = 0°, и к Земле обращено все освещенное полушарие Луны. Полная Луна видна на небе в направлении, противоположном направлению на Солнце (ее эклиптическая долгота отличается от долготы Солнца на 180°). Поэтому полная Луна видна на небе всю ночь; восходит она приблизительно во время захода Солнца, а заходит около момента его восхода. После полнолуния Луна начинает «убывать», с западной стороны ее диска появляется «ущерб», который постепенно растет, так как с каждым днем с Земли вндна все меньшая часть освещенного полушария Луны. Приблизительно через семь дней после полнолуния Луна снова видна в виде полукруга. Наступает последняя четверть. В это время Луна находится в западной квадратуре, ф = 90°, и к Земле снова обращены половина освещенного и половина неосвещенного полушария Луны. Но теперь Луна отстоит уже на 90° к западу от Солнца и видна во второй половине ночи, вплоть до восхода Солнца. Постепенно ущерб лунного диска увеличивается, Луна снова принимает вид узкого серпа и видна на востоке, в лучах утренней зари, незадолго перед восходом Солнца. Через два-три дня лунный серп исчезает, и Луна снова не видна на небе, так как приблизительно через семь суток после последней четверти опять наступает новолуние. Соединение Луны с Солнцем во время новолуния и противостояние во время полнолуния называются сизигиями.
  
  
  Способ Д. В. Ппсковского, 1966 г. Астроном, профессор Киевского университета Д. В. Пясковский предложил следующий простой способ определения фазы Луны. Продолжительность среднего синодического месяца (периода смены фаз Луны) равна 29,5306 средних суток (приближенно 29d,5) и возраст Луны в разных фазах можно принять следующим: новолуние 0 суток, первая четверть 7 суток, полнолуние 15 суток и последняя четверть 22 суток. Древнегреческий ученый Метон (V век до н. э.) нашел, что фазы Луны повторяются через 19 лет, приходясь на те же даты. Этот интервал почти точно равен 235 лунным месяцам, так как 365,2422 X 19 = 6939,6018 суток, а 29,53059 X 235 = 6939,6886 суток. Разница составляет всего 0,0892 суток или 2,14 часа. Значит, фазы Луны в григорианском календаре будут повторяться в том же порядке каждые 19 лет, но разница будет постепенно накапливаться и приблизительно через 200 лет достигнет целых суток. Если, например, 1 января 1960 г. «возраст» Луны был 2 суток, то через 11 циклов по 19 лет (11 X 19 = 209), т. е. 1 января 2169 г., он будет меньше на 1 сутки. Напротив, 209 лет назад, 1 января 1751 г. он был на сутки больше. Поскольку точность определения возраста Луны составляет примерно 1 сутки (этого вполне достаточно для практических целей), то накопление указанной ошибки в пределах ±200 лет можно не учитывать. Только при больших интервалах времени нужно ее вводить. Для определения возраста Луны для любой даты нужно знать ее возраст 30 ноября каждого года. Условимся обозначать последнее число каждого месяца, как это часто делают астрономы, нулевым числом последующего месяца. Например, 30 ноября равнозначно 0 декабря. Обозначим возраст Луны 0 декабря через В0. Это число будет постоянной величиной для всего следующего года.

Лунный год, т. е. 12 синодических месяцев, равен 354,3674 суток, т. е. на 10,875 суток короче тропического года. Поэтому возраст Луны за год увеличивается на 10,875 суток, а за месяц в среднем на 10,875 : 12 = = 0,90265 суток. Поэтому можно принять, что по истечении месяца возраст Луны увеличится на одни сутки. Значит, если для 0 декабря (т. е. 30 ноября) ее возраст был равен В0 суток, то через месяц, 0 января, он будет равен В0+ 1 суток, а 0 февраля В0 + 2 суток и т. д. Поэтому для нулевого числа каждого месяца возраст Луны будет равен

(Отсюда становится понятным, почему в качестве постоянного числа В для данного года удобно брать возраст Луны на 30 ноября предыдущего года.) За один день возраст Луны увеличивается на сутки. Значит, для даты Q он будет равен

Если при суммировании получится число, большее 30, то нужно отбросить 29,5 или 59 суток. Если мы посчитаем величину В для 30 ноября, то получим

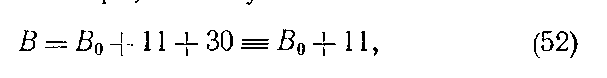
т. е. для каждого следующего года В0 увеличивается на 11 суток. Таким образом, определив величину Ва для какого-либо года, например, заглянув в календарь, нетрудно найти ее значение для следующих лет. Так, установив, что в 1962 г, новолуние было 27 ноября, мы получим следующую табличку:

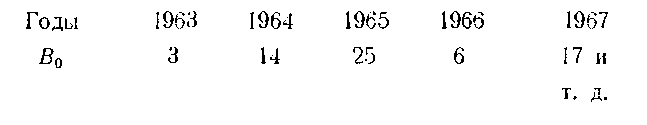
Определим, например, возраст Луны во время максимума потока Персеид 12 августа 1965 г. и 1966 г.:

для 1965 г. В = 25 + 8 + 12 = 45 (возраст 15 суток -~ полнолуние), для 1966 г. В = 6 + 8 + 12 = 26 (за четверо суток до новолуния). Покажем теперь, как определить В0 для отдаленной эпохи. Так как фазы Луны повторяются через 19 лет (например, полнолуние приходится на 5 февраля 1947 г., 5 февраля 1966 г., 5 февраля 1985 г.), то повторяются И постоянные числа В0. Учитывая, что в цикле Метона 19 лет, можно каждому году в цикле приписать номер, равный остатку от деления номера года на 19, а затем для каждого номера в цикле найти соответствующее значение В0.

В современном цикле одним из нулевых годов, т. е. имеющим номер 0, является год 1957-й (1957 делится без остатка на 19), для него В0 = 27. Такими же являются годы 1976, 1995, 2014 и т. д. Отсюда без труда получаем постоянные числа для всех годов в цикле:

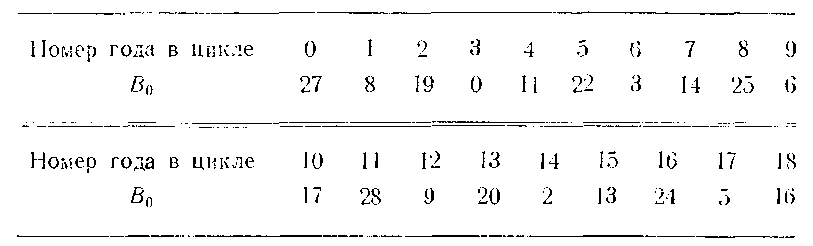
Все расчеты для определения возраста Луны производятся по формуле (51). Только в том случае, если нас интересует возраст Луны для эпохи, удаленной от современной более чем на 200 лет, придется вводить дополнительную поправку в 1 сутки за каждые 200 лет. Для предыдущих веков она положительна, а для последующих отрицательна. Проверим, могло ли быть (а это утверждается в летописи) затмение Солнца 12 октября 1605 г. Здесь при расчете по основной формуле (51) требуется дополнительная поправка в двое суток, так как указанный год отстоит от современной эпохи почти на 400 лет. Разделив 1605 на 19, получим номер года в цикле 9, ему соответствует В0 = 6. Поэтому В = 6+ 10 + 12+2 = 30 - действительно Луна была в новолунии. Другой пример. Известно, что ближайшее полное затмение Солнца в Москве произойдет 16 октября 2126 г. Убедимся, что в этот день Луна будет в новолунии. Разделив номер года на 19, получим остаток, а значит, и комер года в цикле, равный 17. Для него В0 = 5, дополнительная поправка - одни сутки. Следовательно, В = 5 + 10 + 16 - 1 = 30, - Луна в новолунии. Таким образом, предлагаемый способ позволяет определить возраст Луны для любой даты в любом году. Чаще всего приходится определять возраст Луны для какой-либо даты текущего года. Для этого достаточно запомнить постоянное число для данного года, например, число В0 - 3 для 1982 г.