Экспериментальная часть

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«Ивановский государственный энергетический университет имени В.И. Ленина»

Кафедра электропривода и автоматизации промышленных установок

ЛАБОРАТОРНАЯ РАБОТА № 3

по курсу «Теория автоматического управления»

«Исследование установившихся режимов линейных САУ»

Выполнили: студенты ЭМФ

гр. 3-3

Миколаенко Е.А

Шеманаев Д. С.

Проверил: Спичков Ю.П.

Иваново 2014

Цель работы: изучение установившихся режимов линейных САУ.

Теория

Как всякая динамическая система, система автоматического управления может находиться в одном из двух режимов – установившемся (статическом) и переходном.

Установившийся режим – это режим, при котором система находится в состоянии покоя вследствие того, что все внешние воздействия (управляющие и возмущающие) и параметры самой системы не изменяются во времени.

Исследование системы в установившемся режиме позволяет оценить качество регулирования выходной переменной с точки зрения отклонения от заданного значения при изменении возмущающего воздействия. Если стоит задача стабилизации выходной переменной, то говорят о статической ошибке системы, то есть об отклонении регулируемой переменной от заданного значения при приложении определенного возмущающего воздействия. При исследовании САУ важно установить связь между параметрами системы и величиной статической ошибки, чтобы иметь возможность снижения этой ошибки путем изменения определенных параметров системы. В некоторых случаях практического применения систем автоматического управления наличие статической ошибки регулирования недопустимо. Созданию систем, не имеющих статической ошибки регулирования, в теории автоматического управления уделяется большое внимание.

Системы автоматического управления, в которых имеется определенная статическая ошибка регулирования, называют статическими САУ. Системы, в которых статическая ошибка отсутствует, называют астатическими.

Выполним анализ установившегося режима применительно к замкнутой САУ с отрицательной обратной связью, структурная схема которой показана на рис. 1.

Рис. 1. Структурная схема САУ

Связь между регулируемой переменной Z(s) и воздействиями: управляющим воздействием X(s) и возмущающим воздействием Y(s), для разомкнутой и замкнутой САУ можно получить по структурной схеме (рис. 1), используя принцип суперпозиции и правила эквивалентного преобразования структурных схем.

Регулируемая переменная в разомкнутой системе определяется следующим образом:

.

Регулируемая переменная в замкнутой системе определяется следующим образом:

.

Рассмотрим САУ в установившемся режиме. По определению установившегося режима

Тогда изображения по Лапласу имеют вид:

Для нахождения установившихся значений регулируемой величины в замкнутой и разомкнутой системах воспользуемся теоремой преобразования Лапласа о предельных значениях:

Установившиеся значения регулируемой величины в разомкнутой и замкнутой системах имеют вид:

,

.

Введем обозначения:

- коэффициент усиления разомкнутой САУ

;

- установившееся значение регулируемой переменной при отсутствии возмущающего воздействия

;

- соотношение управляющих воздействий в разомкнутой и замкнутой системах

.

В результате подстановок получаем уравнения статических характеристик разомкнутой и замкнутой систем:

,

.

Графики статических характеристик разомкнутой и замкнутой САУ показаны на рис. 2.

Рис. 2. Статические характеристики

Статические характеристики иллюстрируют влияние возмущающего воздействия на регулируемую величину.

Статическая ошибка регулирования в САУ определяется следующим образом:

.

При , когда определим соотношение и :

.

Обеспечивая высокое значение , можно существенно снизить статическую ошибку регулирования. В этом, по сути дела, и заключается эффект введения в САУ отрицательной обратной связи. С величиной статической ошибки регулирования связано важное для САУ понятие диапазона регулирования, характеризующее пределы изменения значений регулируемой переменной, соответствующих конкретному уровню возмущающего воздействия:

На рис. 3 показаны статические характеристики замкнутой системы, соответствующие верхней и нижней границам диапазона регулирования.

Рис. 3. Определение диапазона регулирования

Возможные пределы регулирования ограничиваются сверху максимально допустимыми значениями, а снизу – требуемой точностью. Очевидно, что увеличение коэффициента усиления разомкнутой системы ведет к снижению ошибки регулирования и увеличению диапазона регулирования.

В системах автоматического управления различают два случая:

1. , такие системы называю статическими. Здесь всегда сохраняется влияние возмущения на установившееся значение регулируемой величины, определяемое статической ошибкой (статизмом) системы.

2. , такие системы называют астатическими. В такой системе влияние возмущения на установившееся значение регулируемой величины отсутствует, отсутствует статическая ошибка регулирования.

На практике бесконечное усиление в САУ обеспечивается не за счет усилителей, а за счет использования особого вида передаточной функции .

Эта передаточная функция должна иметь нулевой полюс, то есть соответствовать форме

Легко видеть, что в этом случае

.

Нулевой полюс обеспечивается введением интегрирующего звена в передаточную функцию .

Отметим, что обеспечить можно лишь за счет динамического звена . Использование ведет к сохранению статической ошибки, дает тождественное нулевое значение регулируемой величины.

Подставив в уравнение, описывающее замкнутую систему, , получим

.

Уравнение статической характеристики в этом случае имеет вид:

.

Если же в САУ реализована единичная обратная связь, , то

.

В астатических системах автоматического управления диапазон регулирования теоретически равен бесконечности, на практике он ограничивается величиной динамических ошибок регулирования при малых значениях регулируемой величины.

В заключение рассмотрения установившихся режимов следует оценить связь параметров статических и астатических систем автоматического управления с динамическими режимами. Без учета этого вопроса может оказаться так, что синтезированная из условий обеспечения статических режимов система будет иметь неудовлетворительные динамические характеристики. В некоторых случаях можно даже получить неустойчивую замкнутую систему.

Рассмотрим влияние коэффициента статической системы на устойчивость. Для этого положим в системе, показанной на рис. 1

,

,

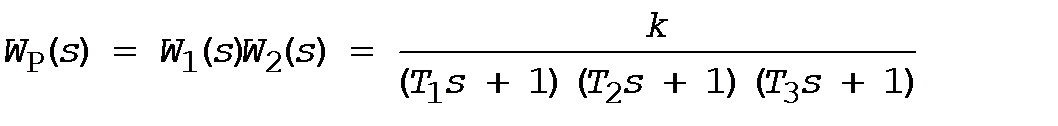где . Пусть с коэффициентом мы имеем устойчивую замкнутую систему, имеющую достаточные запасы устойчивости по модулю и фазе. Увеличим до значения и оценим изменение устойчивости системы с помощью частотного критерия Найквиста по логарифмическим амплитудным и фазовым частотным характеристикам разомкнутой системы, графики которых показаны на рис. 4.

Рис. 4. Исследование устойчивости статической системы

Из анализа ЛАЧХ и ЛФЧХ разомкнутой системы видно, что увеличение коэффициента усиления разомкнутой системы не изменяет ЛФЧХ, а ЛАЧХ параллельно смещается по оси ординат в сторону увеличения. При этом запасы устойчивости по модулю и фазе уменьшаются, при дальнейшем увеличении коэффициента усиления система может стать неустойчивой. Поэтому, повышение точности регулирования в статических системах, осуществляемое увеличением коэффициента усиления разомкнутой системы, должно обязательно сопровождаться проверкой системы на устойчивость с использованием известных методов.

Рассмотрим астатическую систему, в которой

,

,

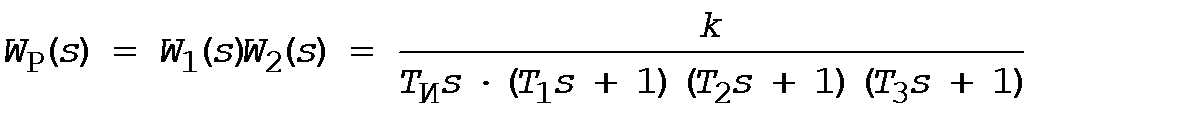где - постоянная времени интегрирующего звена, включенного в . Рассмотрим, как изменяется устойчивость системы при преобразовании ее из статической в астатическую на основе использования критерия Найквиста (рис. 5).

Рис. 5. Исследование устойчивости астатической системы

Как показывают логарифмические характеристики, введение интегрирующего звена, превращающее системы в астатическую, существенно изменяет динамические свойства системы в целом. Введение интегрирующего звена смещает ЛФЧХ на , а наклон ЛАЧХ на каждом участке увеличивается на 20 дБ/дек. На рис. 5 показан случай, когда астатическая система оказывается на границе устойчивости. Изменяя величину постоянной времени интегрирующего звена , можно получить устойчивый режим работы системы, для этого необходимо увеличивать . Следует отметить, что быстродействие астатической системы в нашем случае будет ниже, так как существенно уменьшается частота среза.

Из рассмотренного выше можно сделать вывод, что решение задач точности регулирования в установившихся режимах необходимо сопровождать глубоким анализом динамики системы: исследованием с помощью известных критериев устойчивости системы и анализом качества переходных процессов в системе.

Экспериментальная часть