Поверхности равного потенциала. Эквипотенциальные поверхности.

1).

, , , ,

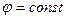
Потенциальная поверхность

2). Потенциальная поферхность замкнута.

3).

,

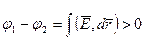
БИЛЕТ 4. Теорема Остроградского-Гаусса для Е (для вакуума) в интегральной форме.

Доказательство:

БИЛЕТ 5. Теорема Остроградского-Гаусса для Е (для вакуума) в дифференциальной форме.

ТОГ в дифференциальной форме

Нижняя грань:

Верхняя грань: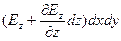

Лев:

Прав:

Перед: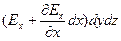

Зад:

Цилиндрическая система координат:

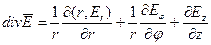
БИЛЕТ 6. Диполь. Дипольный момент. Диполь в однородном и неоднородном электростатическом поле.

БИЛЕТ 7. Классификация диэлектриков. Поляризованность (вектор поляризации). Диэлектрическая восприимчивость. Расчет Р для однородного диэлектрика в однородном электростатическом поле.

БИЛЕТ 8. Теорема Гаусса для поляризованности (в интегральной и дифференциальной форме).

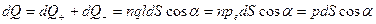
вышедший из области, ограниченной поверхностью.

БИЛЕТ 9. Теорема Остроградского-Гаусса для диэлектрика. Вектор электрического смещения. Относительная диэлектрическая проницаемость вещества.

Связанными зарядаминазываются заряды, которые входят в состав атомов и молекул, а также заряды ионов в кристаллических диэлектриках с ионной решеткой.

Свободными зарядаминазываются заряды, не связанные с перечисленными выше частицами вещества.

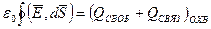
- вектор электрического смещения

.

Связь 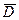и .

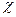- относительная диэлектрическая проницаемость среды. Для вакуума: 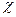=0.