Анализ: Антон Веберн, ор.7 №3

В книге "Структура атональной музыки" Форт представил целостные анализы нескольких произведений – это Четыре пьесы ор.7 №3 А.Веберна²⁰, Altenberg Lieder op.4/3 А.Берга, Священная пляска (финал Весны священной) И.Стравинского, Farben op.16/3 А.Шенберга. Язык аналитического изложения Форта с одной стороны ориентирован на подготовленного читателя и потому может быть воспринят как слишком лаконичный, а с другой – он максимально приближен к языку математических формул, предельно абстрагирующих музыкальную теорию. Мы приводим текст аналитических разборов Форта в несколько адаптированном виде, в том числе за счет добавления нотных примеров, необходимых для пояснения сложного текста авторского анализа. Вся структура сочинения объединяется рядами 6-Z6/38, 6-Z13 и 4-9:

Пример 21*

Их взаимоотношения видны на таблице комплексов, образуемых этими рядами:

За исключением трихордов, каждый ряд связан прежде всего либо с 6-Z6/38, либо с 6-Z13. Единственное исключение составляет ряд 4-9, который связан с обоими, объединяя, таким образом, два различных гексахордовых комплекса. Можно предположить, что эта особенность структуры целого отражена также и в родстве комплексов отдельных секций, и в родстве объединенных секций.

И действительно, наиболее ярко это выражено в отдельных секциях. В предыдущем примере мы видим членение композиции на четыре секции, обозначенные буквами А, В, С и D. Для трех из них – B, С и D – существует связующий ряд 6-Z13. В секции В, где он появляется вместе с рядом 6-Z38, эти два гексахорда оказываются самым непосредственным образом связаны с рядом 4-9 (фигура скрипки).

Рассмотрим теперь соотношения секций попарно с точки зрения комбинации комплексной структуры, а также с точки зрения происхождения рядов, явного и скрытого.

Между секциями А и В сильнейшая связь образуется рядами 6-Z6 и 6-Z38:

· Ряд 6-Z6 целиком охватывает секцию А

Пример 22

· ряд 6-Z38 в В выведен из 6-Z6, являясь его дополнением, путем транспозиции на 9: 6-Z38=T(6-Z6, 9):

Пример 23

Инвариантный ряд состоит из 5 высот: [8,9,10,2,3], образуя ряд 5-7:

Пример 24

Как видно в Примере 21, ряд 5-7 присутствует и в секции А, и в секции В. При этом в секции В оба раза он дается в инверсии:

Пример 25

Обе формы 5-7 в данном случае являются субрядами (сегментами) 6-Z38 (в инверсионной форме). В свою очередь 4-9 является субрядом для 5-7 (см.). Аналогичную "связующую" функцию ряд 4-9 в секции А – с рядами 6-Z6 и 5-7, но там это не выглядит столь значительно, как в В.

Секция В делится на две большие сегмента: первый охватывает ряд 8-Z15, второй – 8-28:

Пример 26

В рамках целостной структуры комплекса сочинения это представляет перемещение от комплекса вокруг 6-Z6/38 к комплексу вокруг 6-Z13. Таким образом, хотя музыкальная "поверхность" реально изменена минимально, мы отчетливо наблюдаем смену структуры, лежащей в основе. Этот "сдвиг" тем более очевиден, что формы ряда 5-7 (субряды 8-Z15) меняются на формы 5-19:

Пример 27

При этом ряд 4-9 остается, как объединяющий компонент (см. Пример 21).

Суммируя вышеизложенное:

1) первая часть секции В производна от А;

2) вторая часть секции В представляет новый субкомплекс. Примечательно, что это происходит это с минимальными изменениями в звуковысотном составе ряда – фактически, только через появление трех нот у фортепьяно (es, d и fis).

Секция С в большой степени может рассматриваться как продолжение секции В. Здесь снова встречается ряд 4-9 (на той же высоте):

Пример 28

Дополнительные компоненты формируют большой сложный сегмент – 7-4, который содержит ряд 6-Z13, недавно отмеченный пунктиром в Примере 21:

Пример 29

Из трех пар несмежных секций (А+С, A+D и B+D) только две оказываются тесно связаны: секция А объединяется с С посредством ряда 4-9, также как это было в А+В. В регистровом и высотном отношении ряд 4-8 в А соответствует форме 4-8 в С. Родственность секций обеспечивается также рядом 3-1 (в А – первый составной сегмент, а в С – фортепианная партия):

Пример 30

Полный состав секции D — 6-Z13 — выводится из двух форм 6-Z13 секции В путем транспозиции:

Пример 31

Получающийся инвариантный субряд – [0,3,6], из которого pc3 и pc6 специально выделены в нижнем регистре в конце секции. Это дает разделение 6-Z13 и отделения от него 4-18 (см. Схему 1). Этот ряд 4-18 является членом К(6-Z13). Это, однако, не первое его появление – он встречается 8 раз во второй половине секции В, как субряд для 8-28:

Пример 32

Заключение

Там, где кончается действие известных нам теории, метод рядов может оказать эффективную помощь: именно в том разделе, где звуковысотность требует своего нового обозначения. Математическая точность теории рядов, приспособленной к условиям многопараметрового анализа, может помочь унифицировать музыкальный материал вне зависимости от его гармонической сложности. Фиксируя структуру и ее элементы, теория дает очень простой язык для их названия – цифровой. И такое повышенное внимание к исчислительности здесь может обернуться положительной стороной. Основную дихотомию, существующую в музыкальном исследовании, можно выразить так: музыкальная теория – абстрактна, музыкальный анализ – конкретный. Теорию рядов следует понимать как инструмент (то есть – абстрактный предмет), с помощью которого можно изучить конкретную музыкальную структуру. Переходя от абстрактной теории к подробностям музыкального разбора, аналитик должен точно решать, как много теории необходимо применить, и как эту теорию интерпретировать, чтобы она соответствовала цели данного анализа.

Приложение

Таблица рядов²¹

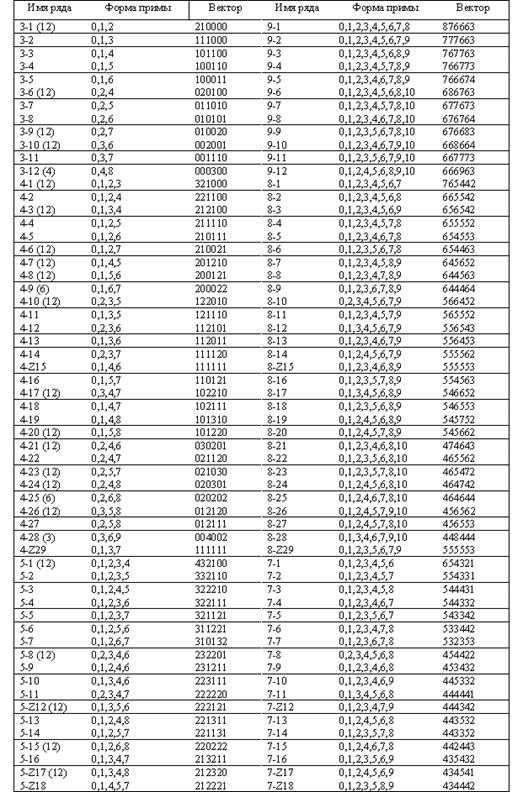
1В американском музыкознании разделение на специальности носит особый характер, что связано с долгим отсутствием соответствующей школы. Вплоть до второй половины ХХ века американское музыковедение носило скорее "исторический" характер, а как только теория музыки начала проявлять себя как самостоятельная область музыкальной науки – ее резко противопоставили собственно музыковедению. На сегодняшний день наука о музыке в США делится на музыковедение (musicology), этномузыковедение и теорию музыки, в то время как в большинстве стран (в том числе и в России) музыковедение – это и теория, и история музыки (а также музыкальная этнография и критика).

2 Context and Continuity in an Atonal Work // Perspectives of New Music 1963, 1/2 (72-88); A Theory of Set-Complexes for Music // Journal of Music Theory 1964, № 8/2 (136-184); The Domain and Relations of Set-Complex Theory // Journal of Music Theory 1965, № 9 (173-180); Sets and Non-Sets in Schoenberg's Atonal Music // Perspectives of New Music 1972, № 11 (43-64).

3 Allen Forte. The Structure of Atonal Music. – Yale university Press, 1973.

4 Слово "гемитоника" (от греч. hemitonion— полутон) наилучшим образом фиксирует главную музыкальную сущность системы – не то, что ступеней 12, а то, что единицей системы является полутон.

5 Здесь гемитоника вступает в конфликт с классической 7-ступенной тональность. Ведь, например, gis теперь обозначает не повышение соль на полтона, но принципиально новую ступень. Но, будучи написанным как gis, он остается как бы "зависим" от g.

6 Поскольку корни теории рядов – математические, то и большинство новых терминов и условных обозначений переносятся в музыку из соответствующих разделов математики.

7 t=ten (10), e=eleven (11)

8 A.Forte. The Structure of Atonal Music, p.3.

9 В англо-русском словаре под редакцией В.К.Мюллера (1996) слово set как существительное имеет 21 значение (в том числе — набор, комплект, теннисный тайм, направление, общество, стойка собаки, сцена, художественное оформление, укладка волос и т.д.), row —6 (ряд, гребля, прогулка на лодке, гвалт, ссора, нагоняй), series — 4 (ряд, серия, отдел, последовательное соединение).

10 Однако, нам представляется нецелесообразным использовать "правильный" перевод по ряду причин. Во-первых, слово множество крайне непрактично для употребления и не может прижиться в русском языке как термин (в отличие от однослоговых set и ряд). Во-вторых, когда американские теоретики музыки записывают этот set, они всегда делают это в виде горизонтального ряда, то есть – звукоряда. В этом есть правильный смысл – наше понимание этих рядов идет от свойств этого ряда. Вместе с тем, понятие "множество" имеет еще один оттенок смысла, который не должен пропадать: сущность set как ряда подразумевает не только его горизонтальное изложение в виде мелодии, но и как созвучия, аккорда. А поскольку смысл понятия set подразумевает в равной степени и то, и другое, то и мы в случае необходимости можем проводить эти тонкие различия: set в виде мелодии мы называем ряд (в связи с термином "звукоряд"), а вертикальную группу, большей частью подобную кластеру, - просто группа.

11 Пермутация – процедура, впервые ярко представленная в серийной музыке, представляет собой изменение порядка тонов серии.

12 Для додекафонной серии форма примы – первоначальная форма, из которой выводятся новые (производные) формы.

13 От лат. cardinal — количественный.

14 Эквивалентными могут быть только ряды с одинаковым кардиналом, то есть – с одинаковым количеством звуков.

15 Примеры, заимствованные из книги А.Форта "Структура атональной музыки" помечены *.

16 Прототипом ряда и его дополнения можно считать тропы австрийского композитора Й.М.Хауэра (Hauer Josef M. "Zwölftontechnik". – Wien, Universal Edition, 1926). Тропы Хауэра – это 12-звуковые ряды (всего – 44), разделённые на две группы по 6 звуков ("шестёрки"). Каждая шестерка является взаимодополняющей для другой.

17 Буква Z не имеет специального значения, кроме того, что она указывает на необычность этого ряда.

18 Форт говорит о 19 Z-парах – он не считает ряды-дополнения.

19 Буква R – сокращенное англ. relation (подобие). Нижние индексы, указанные далее, обозначают соответственно: p – pitch (звук); 0, 1 и 2 – возрастание степени интервального родства.

20 В 1999 году вышла в свет книга Форта, целиком посвященная анализам музыки Веберна ("The Atonal Music of Anthon Webern", Yale Univ Press, 1998).

21 Allen Forte "The Structure of Atonal Music", pp. 179-181.

* Звездочка около К – К* – обозначает, что в данном комплексе сохраняется родство включения.