Байеса.

Классическое определение вероятности

Если множество всех исходов опыта Ω – конечно, а сами исходы несовместны, равновозможны и образуют полную группу, то вероятность события A Ì Ω равна отношению количества благоприятных исходов опыта к количеству всевозможных исходов.

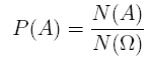
Определение условной вероятности события

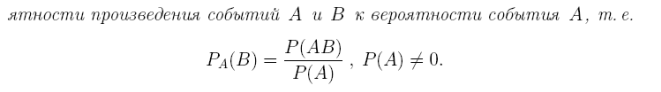
Определение независимых событий

Определение несовместных событий.

События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Теорема сложения, теорема умножения,

Формула полной вероятности, формула

Байеса.

1. Теорема сложения вероятности двух совместных событий:

2. Теорема сложения вероятности трех совместных событий:

3. Теорема сложения вероятности двух несовместных событий:

4. Теорема сложения вероятности трех несовместных событий:

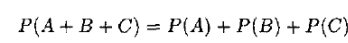
5. Теорема умножения вероятностей двух совместных событий:

6. Теорема умножения вероятностей трех совместных событий:

7. Теорема умножения вероятностей двух независимых событий:

8. Формула полной вероятности события:

9. Формула Байеса (формула уточнения гипотез)