
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эффект Холла. Большинство современных датчиков, которые используются в автомобилестроениях для измерения скорости
Большинство современных датчиков, которые используются в автомобилестроениях для измерения скорости, основаны на эффекте Холла.
Эффектом Холла называется появление в проводнике с током плотностью j, помещённом в магнитное поле Н, электрического поля Ех, перпендикулярного Н и j. При этом напряжённость электрического поля, называемого ещё полем Холла, равна
Ex = RHj sin a, (1):
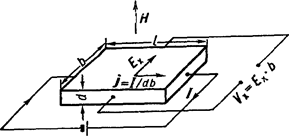
Рис 1.1
где a угол между векторами Н и J (a<180°). Когда H^j, то величина поля Холла Ех максимальна: Ex = RHj. Величина R, называемая коэффициентом Холла, является основной характеристикой эффекта Холла. Эффект открыт Эдвином Гербертом Холлом в 1879 в тонких пластинках золота. Для наблюдения Холла эффекта вдоль прямоугольных пластин из исследуемых веществ, длина которых l значительно больше ширины b и толщины d, пропускается ток:
I = jbd (см. рис.);
здесь магнитное поле перпендикулярно плоскости пластинки. На середине боковых граней, перпендикулярно току, расположены электроды, между которыми измеряется ЭДС Холла Vx:
Vx = Ехb = RHj/d. (2)
Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на обратное, то Холла эффект относится к нечётным гальваномагнитным явлениям.
Простейшая теория Холла эффекта объясняет появление ЭДС Холла взаимодействием носителей тока (электронов проводимости и дырок) с магнитным полем. Под действием электрического поля носители заряда приобретают направленное движение (дрейф), средняя скорость которого (дрейфовая скорость) vдр¹0. Плотность тока в проводнике j = n*evдр, где n — концентрация числа носителей, е — их заряд. При наложении магнитного поля на носители действует Лоренца сила: F = e[Hvдp], под действием которой частицы отклоняются в направлении, перпендикулярном vдр и Н. В результате в обеих гранях проводника конечных размеров происходит накопление заряда и возникает электростатическое поле — поле Холла. В свою очередь поле Холла действует на заряды и уравновешивает силу Лоренца. В условиях равновесия eEx = еНvдр, Ex =1/ne Hj, отсюда R = 1/ne (cмз/кулон). Знак R совпадает со знаком носителей тока. Для металлов, у которых концентрация носителей (электронов проводимости) близка к плотности атомов (n»1022См-3), R~10-3(см3/кулон), у полупроводников концентрация носителей значительно меньше и R~105 (см3/кулон). Коэффициент Холла R может быть выражен через подвижность носителей заряда m = еt/m* и удельную электропроводность s = j/E = еnvлр/Е:
R=m/s (3)
Здесь m*— эффективная масса носителей, t — среднее время между двумя последовательными соударениями с рассеивающими центрами.
Иногда при описании Холла эффекта вводят угол Холла j между током j и направлением суммарного поля Е: tgj= Ex/E=Wt, где W — циклотронная частота носителей заряда. В слабых полях (Wt<<1) угол Холла j»Wt, можно рассматривать как угол, на который отклоняется движущийся заряд за время t. Приведённая теория справедлива для изотропного проводника (в частности, для поликристалла), у которого m* и t их— постоянные величины. Коэффициент Холла (для изотропных полупроводников) выражается через парциальные проводимости sэ и sд и концентрации электронов nэ и дырок nд:
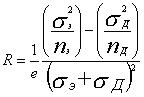 (a) для слабых полей
(a) для слабых полей
(4)
 (б) для сильных полей.
(б) для сильных полей.
При nэ = nд, = n для всей области магнитных полей :
 ,
,
а знак R указывает на преобладающий тип проводимости.
Для металлов величина R зависит от зонной структуры и формы Ферми поверхности. В случае замкнутых поверхностей Ферми и в сильных магнитных полях (Wt»1) коэффициент Холла изотропен, а выражения для R совпадают с формулой 4,б. Для открытых поверхностей Ферми коэффициент R анизотропен. Однако, если направление Н относительно кристаллографических осей выбрано так, что не возникает открытых сечений поверхности Ферми, то выражение для R аналогично 4,б.
Заключение
В работе были рассмотрены общие свойства датчиков измерения скорости и область их применения. Более подробно затрагиваются датчики скорости, объясняется принцип действия на примере конкретных моделей.
Сегодня индустрия полупроводниковых датчиков уже использует второе поколение активных сенсорных технологий, включающих схемы компенсации ошибок и обработки сигнала. Новейшее направление развитие новых цифровых интерфейсов для аналоговых линейных датчиков, оснащенных блоком управления, которые характеризуются как повышенной помехоустойчивостью, так и большей эффективностью коммуникации в реальном времени. Преимуществом датчиков, созданных на основе новых технологий, является их бесконтактность, но, несмотря на это, потенциометры очень не скоро сдадут свои рыночные позиции, поскольку имеют низкую цену и увеличенную надежность.
Список используемой литературы.
1. «Современные датчики. Справочник» Под ред. Дж. Фрайден,— Млсква: Техносфера,2006.
2. http://www.freepatent.ru;
3. Пат. 2150114 Российская Федерация, МПК G01P3/48. Датчик измерения скорости/ Дремов М.В. , Каплунов Г.В., Россия; заявитель и патентообладатель ООО «Счетмаш» . - ; заявл. 30.06.1998; опубл. 20.04.2000.
4. Пат. 2270452 Российская Федерация, МПК G01P3/488. Бесконтактный датчик скорости автомобиля/ Захаров И.С., Яцун С.Ф., Россия; заявитель и патентообладатель «ГОУ КурскГТУ». - ; заявл. 26.01.2004; опубл. 20.02.2006.
5. Пат. 2260188 Российская Федерация, МПК G01P3/488. Бесконтактный датчик скорости автомобиля/ Сысоева С.С., Яцун С.Ф., Россия; заявитель и патентообладатель «ГОУ КурскГТУ» . - ; заявл. 26.01.2004; опубл. 10.09.2005.
6. http://www.luksavtoservis.ru/ds.html;
7. https://blamper.ru/auto/wiki/salon/spidometr-3660
8. https://wikipedia.ru/wiki/
Дата добавления: 2015-01-19; просмотров: 356; Мы поможем в написании вашей работы!; Нарушение авторских прав |