Теоретические сведения. При определении программы места наряду с траекторией движения ОЦТ (см

При определении программы места наряду с траекторией движения ОЦТ (см. Л.р. 1.2) анализируются такие характеристики движения указанной точки, как скорость и ускорение.

Скорость ОЦТ тела – физическая величина показывающая, насколько быстро изменяется его положение в пространстве с течением времени.

Это определение качественное. Для того чтобы получить количественное соотношение, определяющее скорость, иными словами, чтобы получить формулу для вычисления скорости, необходимо вспомнить определения пути и перемещения.

Путь– расстояние, проходимое точкой вдоль траектории.

Как правило, путь обозначается буквой S. Несложно заметить, что путь является скалярной величиной. Действительно, независимо от того, переместились ли мы по траектории из точки A в точку B, или наоборот, пройденный путь будет одним и тем же и будет выражаться одним и тем же числом.

Перемещение– отрезок прямой, соединяющий начальное и конечное положения точки на траектории. Перемещение, обозначаемое ΔS, – величина векторная. Действительно, перемещение из A в B и перемещение из B в A – совсем не одно и то же. При одной и той же длине этих перемещений направления у них противоположные.

Путь S и названные перемещения показаны на рис. 1.3.1.

Рис. 1.3.1

Путь и модуль перемещения совпадают только в том случае, когда движение происходит по прямой линии. Пусть этой прямой линией будет ось Ox.

Рассмотрение материала начнем именно с этого простейшего случая (рис.1.3.2).

Рис. 1.3.2

Итак, ОЦТ тела движется прямолинейно вдоль оси Ox и в моменты времени t₁ и t₂ имеет координаты (x₁,0) и (x₂,0), соответственно. Тогда величина скорости ОЦТ тела определяется по формуле:

V 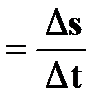, (1.3.1)

где Δs = Δх = x₂ – x₁ есть перемещение ОЦТ тела; Δt = t₂ – t₁ есть промежуток времени, затраченный на его перемещение.

Формула (1.3.1) точна лишь при условии неизменности скорости на всем перемещении Δs. Практически же движение ОЦТ тела между точками, имеющими координаты (x₁,0) и (x₂,0), может происходить по-разному: или сначала быстро, а затем медленно; или первоначально медленно, а затем быстро; или еще каким-либо образом.

Для приближенной оценки величины изменяющейся скорости можно воспользоваться формулой (1.3.1). Однако полученное в этом случае значение скорости является величиной усредненной, относительно которой колеблется истинная скорость ОЦТ тела, перемещающегося между точками с координатами (x₁,0) и (x₂,0). Поэтому переменную по величине скорость V, определяемую по формуле (1.3.1), называют средней скоростью.

Очевидно, что в случае переменной скорости точность ее определения тем выше, чем меньше промежуток времени Δt, так как при очень малых значениях этого промежутка скорость не успевает измениться. В связи с этим наиболее точно скорость определяется для бесконечно малого промежутка времени Δt, стремящегося к нулю. В этом случае мы имеем дело с так называемой мгновенной скоростью:

V_мгн. (1.3.2)

Нетрудно видеть, что (1.3.2) представляет собой производную от пути по времени (сравните с формулой (*), с.12, определяющей производную от функции y по аргументу x).

В общем случае, когда ОЦТ движется по произвольной траектории, положения ОЦТ тела в моменты времени t₁ и t₂ характеризуются точками с координатами (x₁, y₁) и (x₂, y₂), соответственно. Формулы (1.3.1) и (1.3.2) остаются справедливыми, но перемещение Δs определяется по формуле:

Δs = , где Δx = x₂ – x₁, Δy = y₂ – y₁ (см. рис.1.3.3).

Рис.1.3.3

Единицей измерения скорости является м/с.

Ускорение ОЦТ тела – физическая величина показывающая, насколько быстро изменяется его скорость (V) с течением времени.

Количественно ускорение (а) определяется по формуле:

a= 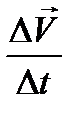, (1.3.3)

где ΔV = V₂ – V₁ – изменение скорости ОЦТ тела в процессе перемещения ОЦТ из точки с координатами (x₁,y₁) в точку с координатами (x₂,y₂); Δt = t₂ – t₁ – промежуток времени, затраченный на перемещение ОЦТ тела, V₁ и V₂ – скорости ОЦТ тела в точках, соответственно (x₁,y₁) и (x₂,y₂).

Формула 1.3.3 позволяет точно определить величину ускорения, неизменного в процессе перемещения ОЦТ тела между точками с координатами (x₁,y₁) и (x₂,y₂).

Аналогично понятиям средней и мгновенной скорости вводятся понятия среднего и мгновенного ускорения. Мгновенное ускорение определяется для случая ускорения, изменяющегося по величине. Оно отличается от среднего ускорения величиной промежутка времени Δt, за который произошло изменение скорости ΔV. В случае среднего ускорения промежуток Δt имеет некоторое конечное значение, а в случае мгновенного ускорения он бесконечно мал. Среднее ускорение можно определить по формуле (1.3.3), а мгновенное ускорение – по формуле:

а_мгн. 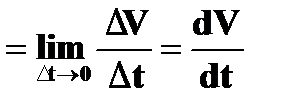(1.3.4)

Единицей измерения ускорения является м/с².

Рассматриваемые в данной лабораторной работе физические величины: перемещение, скорость и ускорение, как уже отмечалось, являются векторными величинами, так как каждая из них характеризуется не только своим значением, но и направлением, то есть не одним, а двумя параметрами. В процессе биомеханического исследования над векторами приходится выполнять те или иные операции. Так, при нахождении скорости (формула (1.3.1)) вектор Δs делился на константу Δt, а при нахождении ускорения разность векторов V₂ – V₁ делилась на эту же константу. Рассмотрим теперь более подробно способы выполнения операций над векторами.

Перечисленные выше (см. с. 11) арифметические операции над векторами: сложение и вычитание, умножение и деление на постоянное число могут выполняться двояко: 1) традиционно, т.е. без использования компьютера и 2) с использованием стандартных компьютерных процедур.

Сложение и вычитание векторов.

1) Традиционный способ (правило параллелограмма).

Сложение и вычитание векторов на плоскости (например, векторов скоростей V₁ и V₂) по правилу параллелограмма производится так. Один из указанных векторов (например, V₁) следует переместить в плоскости чертежа (рис. 1.3.4) параллельно самому себе до совмещения его начала с началом второго вектора.

Полученную таким образом фигуру необходимо достроить до параллелограмма (АВСЕ на рис. 1.3.4). Диагональ АС этого параллелограмма будет суммой векторов V₁ и V₂, а диагональ ВЕ – разностью V₂ и V₁.

Рис.1.3.4

2) Компьютерные процедуры операций сложения и вычитания векторов основаны на представлении векторов наборами проекций на оси координат и выполняются покоординатно. Естественно, что результирующий вектор также будет представлен набором своих проекций на координатные оси. Полученный результат, в случае необходимости, легко представим в виде геометрического вектора (рис. 1.3.5).

Рис.1.3.5

Примечание. В случае отсутствия компьютерной поддержки данный алгоритм может использоваться вручную как альтернатива правилу параллелограмма.

Умножение и деление вектора на постоянное число.

1) Умножение вектора (например, V_1, рис. 1.3.6) на некоторое постоянное число (С) традиционно производится так: число V₁ (модуль вектора V₁) умножается на C, затем строится вектор длиныV₁·C, при этом, если C > 0, то направление вектора V₁·C совпадает с направлением вектора V₁, а если C < 0, то оно является противоположным направлению вектора V₁. Отметим также, что, если ‌│C│>1, то длина вектора V₁·C увеличивается в C раз по сравнению сдлинойV₁, если же │C│<1, то она уменьшается в 1/C раз. Операция деления отдельно не рассматривается, так как деление на C равносильно умножению на 1/C. (На рис.1.3.6 даны векторV₁ и векторыV₁·C, где C=2, -2, 1/2, -1/2)

Рис.1.3.6

2) При координатном задании вектора операции умножения и деления его на постоянное число C выполняются покоординатно (см. с.11). В случае необходимости строится результирующий вектор.

Описанные алгоритмы работы с векторами позволяют рассчитать и в случае необходимости вручную построить векторы скоростей и ускорения ОЦТ тела спортсмена. Необходимо только помнить, что направление скорости всегда совпадает с направлением движения. Для прямолинейного движения ускорение совпадает по направлению с вектором скорости, если движение ускоренное, т. е. V₂>V₁, и направлено в противоположную сторону, если движение замедленное, т. е. V₂<V₁. Отметим также, что если используются приближенные формулы (1.3.1) и (1.3.3), то есть интервалы Δt, Δs,ΔV – конечные, векторы скоростей и ускорения должны исходить из начала вектора перемещения.