
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВВЕДЕНИЕ. К приборостроению относятся две области человеческой деятельности
К приборостроению относятся две области человеческой деятельности. С одной стороны, это часть машиностроения, занятая производством средств измерения, анализа, обработки и представления информации, устройств регулирования, автоматических и автоматизированных систем управления. С другой стороны, это область науки и техники, разрабатывающая средства измерений, автоматизации и системы управления.
Каждая из перечисленных областей настолько обширна и многогранна, что описать их с какой-то степенью подробности не представляется возможным. Тем более что средства измерений и автоматизации развиваются и совершенствуются опережающими темпами относительно других областей человеческой деятельности, определяя направления и скорость научного и технического прогресса человечества. Поэтому далее будут рассмотрены только начальные сведения по средствам измерений и автоматическому управлению, однако, достаточные для общего качественного представления об обсуждаемых темах.
Исторически сначала начали развиваться техника и теория измерений. Она определила развитие научных знаний и обеспечила фундамент современного технического прогресса. Причины определяющей роли измерений в развитии человечества не очевидны и станут понятны из дальнейшего изложения. Пока же можно повторить слова великих ученых [1]:
- «Каждая вещь известна лишь в той степени, в какой ее можно измерить» (У. Кельвин);
- «Наука начинается с тех пор, как начинают измерять, точная наука немыслима без меры» (Д.И. Менделеев).
Последнее всестороннее исследование состояния и потребностей развития измерительной техники было проведено в 2005 - 2006 г.г. Национальным институтом Стандартов и Технологий США (сокращенно NIST) [2]. Приведем краткие сведения из заключительного доклада института.
Авторами были проанализированы состояние и потребности промышленности, медицины и обороны США. О роли измерений можно судить хотя бы по следующим данным: в год в США тратится более 100 миллиардов долларов на измерения в области здравоохрания; в вооруженных силах находится 58 тысяч наименований средств измерения и автоматического управления, обеспечивающих оперативную готовность систем вооружения страны; только полупроводниковая промышленность собирается потратить в 2007 г. на разработку и оснащение измерительной техникой и оборудованием 9 миллиардов долларов.
Результаты проведенной оценки состояния измерительной техники были обобщены и сформулированы в трех положениях:
- Основным препятствием на пути инноваций во всех сферах экономики, медицины, обороны, экологии остаются недостаточная точность методов и средств измерений.
- Практически во всех новых технологиях сдерживающим их развитие фактором служит отсутствие точных и достаточно чувствительных датчиков различных величин, необходимых для реализации новых производственных процессов и создания систем управления новыми технологическими процессами.
- Отсутствие стандартов и эталонов для оценки качества создаваемых технологий, что служит барьером для инноваций в новых развивающихся технологиях.
Отдельно авторы доклада останавливаются на вопросе внедрения нанотехнологий. По прогнозам экономистов рынок продукции нанотехнологий в течение 10 лет превысит 2,5 триллионов долларов. Однако указанная продукция серийно не производится в виду отсутствия необходимых теоретических основ, стандартов и измерительных средств.
Сказанное выше не означает, что в США низкий научный и технологический уровень измерительной техники. Как раз наоборот. Во многих областях специалисты США являются пионерами новых направлений создания теории, методов и средств измерений. Ими создан массовый расходомер (Кориолисов расходомер) высокой точности, разработаны первые сенсорные измерители влажности газов, микропроцессорные системы измерений, космический телескоп «Хаббл», глобальная навигационная система определения положения объектов GPS и т.д.
Поэтому указанные в отчете направления развития измерительной техники необходимо понимать как общую задачу для всех стран, не желающих оказаться (или остаться) в ряду развивающихся.
Системы автоматического управления, включающие как составную часть средства измерений, получили широчайшее распространение во всех областях техники. Задачей систем подобного типа является поддержание неизменными (заданными) значения каких - то параметров процессов управляемых объектов или изменение их по заданному закону функционирования.
Первые из указанных систем поддерживают постоянными напряжение и частоту на выходе электрогенераторов электростанций при изменении потребителями величин нагрузок (отбираемой мощности); состав компонентов и параметры процессов (температура, давление, расход) в химических производствах; высоту, скорость и направление полета самолета, заданного пилотами (автопилот) и т.д.
Системы автоматического управления, выполняющих изменение параметров процессов в управляемых системах по заданным законам функционирования, сложнее первых, однако они позволяют не просто поддерживать заданные режимы, а изменять их по какому-то критерию. Например, по данным о температуре автомобильного двигателя, числу оборотов коленчатого вала автоматически устанавливать соотношение между количеством поступающего воздуха и расходом бензина, обеспечивающих максимальный коэффициент полезного действия двигателя.
Переоценить важность систем автоматического управления невозможно, поскольку они, исключая человека из процессов управления, позволяют выпускать серийную продукцию с гарантированными параметрами при любом объеме производства.
Во многих случаях человек не в состоянии вести управление процессами в силу физиологических ограничений (по скорости реакции на возникшую ситуацию; по габаритам; невозможности нахождения в районе расположения управляемых объектов типа спутника или космической станции).
Все сказанное выше только доказывает важность средств измерений и автоматического управления, не объясняя, как они функционируют и обеспечивают заданные требования. Поэтому далее покажем, на качественном уровне (т.е. без строгого математического анализа), основные положения, лежащие в основе теории измерительных приборов и систем автоматического управления.
Поскольку изложение ведется на качественном уровне, пособие не может служить руководством для проведения анализа или синтеза средств измерения или автоматического управления. Оно дает только общее представление о составе средств измерений и управления, общих принципах функционирования и оценки качества полученных результатов.
Пособие предназначено для первоначального ознакомления с кругом основных тем, подлежащих углубленному изучению в процессе обучения в ВУЗе студентами специальностей:
190100 – Приборостроение;
190200 – Приборы и методы контроля качества и диагностики;
190900 – Информационно-измерительная техника и технологии;
191000 – Технология приборостроения.
1 ОСНОВНОЕ УРАВНЕНИЕ ИЗМЕРЕНИЙ
1.1 ОПРЕДЕЛЕНИЕ ИЗМЕРЕНИЯ
Имеется большое число определений понятия «измерение». Наиболее ясным является классическое определение, данное выдающимся метрологом М.Ф. Маликовым, которое мы и приводим ниже.
Под измерением понимается нахождение значения физической величины путем физического эксперимента сравнения данной физической величины с известной физической величиной того же рода, принятой за единицу измерения.
Запись общей математической формулы процесса измерений и рассмотрение характерных процедур для всех видов измерений требуют предварительного уточнения каждого термина, входящего в данное определение. Вот этим и займемся.
1.2 ФИЗИЧЕСКАЯ ВЕЛИЧИНА
Начнем с понятия «физической величины».
Под физической величиной понимается некоторое свойство физических объектов, качественно общее для них, но в количественном отношении индивидуальное для каждого объекта [3]. Например, линейный размер является свойством космического объекта (звезды, галактики) и отдельного атома. То же самое относится к массе, температуре, вязкости, плотности, электропроводности и другим свойствам физических объектов.
Здесь необходимо сделать несколько уточнений.
Первое. Реальные объекты обладают бесконечным числом свойств. Например, измеряя диаметр детали, мы выбираем один параметр из: массы этой детали, ее длины, температуры, плотности, твердости, химического состава и т.д. Выбирая некоторые из физических величин объекта для измерений, мы мысленно упрощаем сам объект, создаем его модель той или иной степени сложности.
Второе. Модель физической величины, подлежащей измерению, должна быть достаточно подробно описана. Часто это непросто сделать. Для примера, рассмотрим следующую типичную задачу.
Необходимо измерить расход жидкости (например, нефти) в трубопроводе. Что такое расход? Это количество вещества, проходящее через выбранное для наблюдения поперечное сечение трубы за единицу времени. Самая грубая модель: скорость жидкости, умноженная на площадь поперечного сечения трубы (по определению идеальной жидкости) дает величину расхода. Площадь поперечного сечения трубы (модель – окружность) легко определяется по результатам линейного измерения диаметра.
Но непонятно какие объективные данные дают основание утверждать, что труба имеет в поперечном сечении форму окружности, а не, например, эллипса? Далее. Поверхности реальных труб имеет шероховатости. Как они влияют на измерение площади трубы? Нужно это учитывать в принятой модели? Если нужно, то как получить необходимые исходные данные?
Перейдем к определению другой физической величины – скорости. Тут сразу возникает сложная проблема. Дело в том, что труба неподвижна и, следовательно, слои жидкости, примыкающие к стенкам тоже неподвижны. На оси потока, понятно, скорость течения жидкости максимальна. Так какую из скоростей необходимо умножить на диаметр для получения величины расхода? Непростой вопрос, ответ на который оставим до обсуждения основ гидродинамики.
Но, допустим, мы нашли на него ответ. Значит ли это, что задача построения модели измеряемой физической величины решена? К сожалению, приходится ответить отрицательно. Ведь требовалось определить расход вещества, то есть массы жидкости, проходящей через поперечное сечение трубы в секунду, а мы построили модель расхода объема жидкости. Чем необходимо дополнить модель объемного расхода, чтобы получилась модель массового расхода? Необходимо, как известно из курса физики, дополнительно иметь значение (или измерять) плотности жидкости и умножить это значение на значение объемного расхода.
Не вдаваясь в дальнейший анализ модели расхода, отметим одно общее парадоксальное свойство измерительных моделей: прежде чем начать измерения, необходимо знать априорно (до опыта) свойства измеряемой физической величины. В нашем примере это форма поперечного сечения трубы, предельные значения скорости течения, вязкость и плотность жидкости. Получается, что для построения модели подлежащей измерению физической величины нужны результаты предварительных измерений, для выполнения которых опять нужно разработать модели физических величин. А для них где взять исходные данные?
Указанное обстоятельство принципиально характерно для всего процесса познания (в частности, физических объектов): сначала проводят измерения физических величин, описанных грубыми моделями. По мере накопления данных модели уточняют, усложняют и вновь проводят измерения. При таком последовательном процессе результаты измерений приближаются к истинному значению физической величины, достичь которой невозможно. Однако если есть основания полагать, что истинное значение отличается от измеренного на малую величину, несущественную для конкретной измерительной задачи, то полученный результат называется достоверным значением физической величины. Таким образом, достоверные значения физических величин, полученные в результате измерений, служат оценкой неизвестных истинных значений.
Конечно, сразу возникает вопрос: «Как можно сделать заключение о близости истинного значения и достоверного?». Ответ достаточно сложен и отложим его до последующих глав.
1.3 ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
Теперь, зная что такое физическая величина, можно дать предварительный ответ на вопрос о единице физической величины. Предварительный, поскольку более подробно вопрос о единицах физических величин будет рассмотрен в следующей главе. Пока что под единицей физической величины будем понимать физическую величину качественно однородную измеряемой, принятой за единицу.
Особенность единицы заключается в том, что она именована в соответствии с физической величиной: если речь идет о линейном размере, то единица может называться фут, сажень, метр, верста; если о массе, то может называться фунт, килограмм; если о температуре, то может называться кельвин, градус Цельсия, градус Фаренгейта и т.д.
Другими словами, если имеется в виду единица физической величины, то после цифры 1 ставится ее размерность: 1 кг (единица массы килограмм); 1 К (единица температуры кельвин) и т.д.
Выбор единицы до некоторой степени произвольная процедура; именно поэтому до середины 19 века вся наука об измерениях сводилась к объяснению как перевести единицу одной и той же физической величины, принятую в одной стране, в единицу той же величины в других странах. Например, объяснялось, как выразить 1 версту в сухопутных милях или в милях морских и сколько в них саженей (расстояние между кончиками пальцев рук) и косых саженей (расстояние по диагонали между концами пальцев на ноге и на вытянутой руке).
Но если выбор единицы произведен, то должно соблюдаться два условия.
Во-первых, единица должна быть воспроизведена как материальный объект: единица массы в виде гири, единица длины в виде прямолинейного отрезка какого-то материала (одно время, например, единицей длины служила балочка из специального сплава с поперечным сечением в виде буквы х с двумя рисками по ее длине; расстояние между рисками принималось за единицу длины, равную 1 метру) и т.д.
Во-вторых, необходимо обеспечить неизменность размера объекта, определяющего единицу; это требование выполнить крайне сложно и требует усилий многих научных коллективов и использования для создания единиц физических величин последних достижений физики и химии.
В результате выполнения второго требования, техническая реализация единицы физической величины превращается в сложную установку, эксплуатируемую при точно подобранных условиях окружающей среды (температуре, давлении, влажности, уровню электромагнитных помех и т.д.).
Очевидно, что описанной единицей величины невозможно оснастить все измерительные приборы (а их миллионы) по соображениям экономическим, габаритным, эксплуатационным.
Выход из тупика заключается в следующем. В стране создается несколько (обычно 2 - 3) установок, воспроизводящих единицу физической величины с максимально возможной при данном уровне развития науки тщательностью. Эти установки называются эталонамии хранятся они (при соответствующем уровне обслуживания) в институтах метрологии. В измерительных же устройствах применяют более грубые, чем эталоны, устройства реализации единиц. Зато они достаточно просты по устройству, малогабаритны, надежны, просты в эксплуатации. Эти устройства называются мерами.
Приведем примеры мер. Мерами массы служат гири; мерами длины – линейки, концевые плитки (стальные пластины с полированными сторонами); мерами объема – мерные сосуды; мерами времени – периоды колебаний электронных генераторов, стабилизированных кварцем; мерами электрического сопротивления – образцовые сопротивления; мерами электрического напряжения постоянного тока – нормальный элемент (гальванический элемент с платиновыми электродами, помещенными в ртуть и амальгаму кадмия, залитых раствором сульфата кадмия; погрешность воспроизведения значения напряжения – менее 0,0005%) или (более грубые) – электронные стабилизаторы напряжения.
Как обеспечивается передача размера единицы от эталонов к мерам, будет объяснено позднее.
1.4 МАТЕМАТИЧЕСКАЯ ЗАПИСЬ ПРОЦЕССА ИЗМЕРЕНИЙ
После рассмотрения понятий «физическая величина» и «единица физической величины» можно, в соответствии с данным в п. 1.1 определением, записать основное уравнение измерений:
х =Nx·1x, (1.1)
где х – измеряемая физическая величина;
1х – единица физической величины;
Nx – неименованное число (целое или дробное).
Согласно определению измерения (см. п. 1.1) это физический (т.е. выполняемый с использованием приборов) эксперимент сравнения физической величины х с единицей физической величины 1x. Процесс измерения кончается, когда увеличение или уменьшение единицы 1x в Nx раз обеспечивает равенство левой и правой частей уравнения (1).
Уравнение (1), предельно простое в математическом смысле (действительно, умножить любое число на единицу не представляет труда), довольно трудно реализовать технически. Это связано с тем, что необходимо иметь некие технические устройства, которые:
- хранят единицу физической величины (обсужденный вопрос);
- хранят и последовательно задают числа Nx;
- реализуют операцию умножения и операцию уравнивания (представленной в уравнении знаком равенства).
Уравнение измерения может быть записано четырьмя совершенно равноценными с точки зрения математики способами [4]
х - Nx·1x=0; х / Nx - 1x = 0; х / 1x - Nx = 0; х / (Nx·1x) – 1 = 0. (1.2)
С точки зрения техники измерений каждая запись требует другой последовательности измерительных операций и других технических устройств для реализации измерительного прибора.
Рассмотрим, например, построение вольтметра постоянного тока. Если его реализовать по первому выражению из (1.2), то он будет содержать меру напряжения, усилитель с переменным коэффициентом усиления, и нуль - орган (устройство, на выходе которого изменяется скачком напряжение при достижении разностью х - Nx·1x нулевого значения). Если вольтметр реализовывать по второму выражению из (1.2), то он будет содержать вместо усилителя делитель с переменным коэффициентом деления.
Наиболее часто используются в измерительных устройствах преобразования по первому и второму выражению из (1.2). Поэтому для этих случаев представим процесс измерения в виде несколько упрощенных структурных схем [4].

Рассмотрим рисунок 1.1а подробнее.
На вход устройства сравнения подается физическая величина х, которую требуется измерить. На второй вход устройства сравнения подается масштабированное значение меры N(t)·1x. Единица физической величины 1x формируется в блоке «Воспроизведение». Начальное значение неименованного числа N(t) выбирается произвольно, например, равным 1. Запись N(t) как функции времени t подчеркивает тот факт, что это не одно число (результат измерений Nx, который еще нужно определить), а перебор чисел во времени.
После установки первого значения N(t1)·1x устройство сравнения выдает сигнал неравенства (например, электрическое напряжение отрицательной полярности) на блок поиска, который устанавливает на входе в блок масштабирования новое число N(t2), например, 2. Выполняется новый цикл сравнения х с N(t2)·1x. И таким образом будет продолжаться перебор чисел N(tn) до тех пор, пока разность х - N(tn) ·1x не станет равна нулю; в этот момент на выходе устройства сравнения отрицательное напряжение сменится положительным, которое остановит процесс перебора чисел.
Установившееся на выходе устройства поиска число и будет результатом измерения Nx. Теперь остается только указать в каких единицах физической величины полученное неименованное число соответствует входной величине х. Эта процедура на структурной модели обозначена как приписывание размерности. В итоге на выходе измерительного устройства получается именованное число 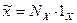 , например, 5 кг, или 1,8 В, или 5 м.
, например, 5 кг, или 1,8 В, или 5 м.
Рассмотренные понятия физических величин, единиц физических величин, процедур измерений дают начальное представление об обсуждаемых вопросах, но далеко их не исчерпывают. Поэтому далее (как в процессе познания) мы будем вновь возвращаться к вопросам описания моделей физических величин, построения измерительных устройств и методам измерений.
1.5 ПОЗНАВАТЕЛЬНЫЙ СМЫСЛ ИЗМЕРЕНИЙ
Ранее было выяснено, что результатом измерений является именованное число. В чем же смысл проведения измерений и получения именованных чисел? Ответ состоит в следующем.
Измерения позволяют заменить физические величины (заряд и массу электрона; объем, давление, температуру газа; объемный расход, температуру, вязкость потока нефти и т.д.) числом, тем самым использовать для анализа явлений объективного мира всю мощь математического анализа. Другими словами, имея результаты измерений, можно обнаружить связи отдельных величин физических объектов между собой и записать их в форме уравнений. Например, закон Ома связывает между собой электрические ток, напряжение и сопротивление; уравнение Клапейрона – давление газа, занимаемый им объем и температуру; уравнение Бернулли – потенциальную и кинетическую энергию движущейся жидкости и т.д.
Анализ полученных уравнений позволяет строить научные предположения (гипотезы) о еще не известных свойствах материальных объектов. Далее следует экспериментальная проверка выводов из гипотез и если результаты измерений подтверждают предположения, то гипотеза переходит в разряд научных теорий. Приведем несколько примеров.
На какой базе была создана термодинамика? На результатах измерений параметров газов, выполненных Гей-Люссаком, Шарлем, Мариоттом, Джоулем, Кельвиным. Проведению исследований свойств газов предшествовало изобретение Г. Галилеем термометра и его учеником Э. Торричелли барометра (измерителя давления газа).
Результаты измерений Ампера и Фарадея, позволившие выяснить основные свойства электрического и магнитного полей, легли в основу теории электродинамики Максвелла.
Основные законы движения небесных тел Кеплер вывел из анализа таблиц измерений положения звезд и планет, выполненных астрономом Брегом.
Эйнштейн начал разработку теории относительности после того, как измерения скорости света, выполненные Майкельсоном и Морли, показали ошибочность предыдущих теорий о свойствах пространства.
Периодическая система элементов Менделеева базируется на измеренных значениях атомных весов и зарядов ядер атомов химических элементов.
О том, что наша Вселенная расширяется известно благодаря измерениям смещения частот световых лучей, приходящих от звезд, выполненных астрономом Э. Хабблом. Но если Вселенная расширяется, то когда–то она была сжата в невероятно плотный объект малого размера? Можно ли это подтвердить? (Как говорил Д.И. Менделеев: «Сказать - то можно что угодно, а ты поди-ка докажи»). Дальше рассуждения шли следующим образом. Если предположить, что началом расширения был взрыв сверхплотного объекта, то в момент взрыва (начало расширения) было только электромагнитное излучение (вещество начало образовываться позднее), остатки которого должны дойти до наших дней. Теоретики даже придумали ему название – реликтовое излучение. В 1964 г. два американских радиофизика Р. Вильсон и А. Пензиас, измеряя параметры космического радиоизлучения, обнаружили предсказанное реликтовое излучение.
Выводы теорий используются прикладной наукой для создания машин, аппаратов и различных видов продуктов промышленности. При этом контроль технологических процессов, свойств полуфабрикатов и готовых изделий невозможен без проведения миллиардов измерений.
Таким образом, можно констатировать, что вся мощь современной науки и техники базируется на измерениях.
К счастью, история сохранила для нас имя ученого, на чьих работах базируется вся мощь самих измерений. Это Галео Галилей, предложивший использовать измерения как средство познания окружающего мира, основоположник разработки измерительных преобразователей, изобретатель измерителя температуры и телескопа.
Завершим данный раздел заветом, оставленным Г. Галилеем последующим поколениям ученых: «Измерять все, что может быть измерено, и делать измеримым то, что измерить нельзя».
2 МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
2.1 ОБЩИЕ СООБРАЖЕНИЯ ПО ВЫБОРУ СИСТЕМЫ ЕДИНИЦ
В п. 1.3 были кратко рассмотрены единицы физических величин. Там же было указано, что исторически в каждой стране произвольно выбирались значения единиц, а для целей научного обмена и торговли составлялись обширные таблицы перевода одних единиц в другие.
По мере развития техники выявился еще больший недостаток существовавшего положения – несогласованность единиц (или, как говорят метрологи, отсутствие когерентности единиц). Несогласованность выражалась в том, что вычисленная по разным формулам одна и та же физическая величина имела различное числовое значение. Например, килограмм обозначал в одних системах массу тела, а в других – силу притяжения к Земле (вес тела). И если необходимо было вычислить силу по второму закону Ньютона, то приходилось уточнять о каких килограммах идет речь и вводить переводной коэффициент (в данном случае равный ускорению свободного падения).
Третья проблема частично затрагивалась в п. 1.3. Речь идет о стабильности физической реализации размера единицы. Действительно, если нет стабильного эталона единицы, то с чем сравнивать меры рабочих средств измерения? Что эти меры будут характеризовать?
Последняя проблема не решена до настоящего времени, но путь решения известен – выбор для эталонов стабильных физических процессов. В частности, излучения возбужденных атомов. Например, эталон метра – это (схематично) кварцевая трубка с газом криптоном низкого давления. Сквозь криптон пропускают электрический ток, возникает разряд и газ начинает светиться. Из всего излученного спектра света выделяют составляющую одной длины волны (оранжевая линия) и, с помощью интерферометра, подсчитывают число длин волн света при перемещении интерферометра на специальной каретке. Когда каретка сместится на 1650764 длин волн, то пройденное расстояние будет единицей длины – один метр.
В эталоне частоты и времени так же используют излучение, но паров цезия и суммируются не длины волн, а количество периодов колебаний световой волны; одной секунде соответствует 9192631770 периодов.
Принципиальное отличие эталонов длины и времени от, например, эталона массы килограмма (специально выполненная гиря) заключается в том, что в любом месте в любое время длины волн и частоты излучения атомов постоянны, а масса гири переменна (зависит от количества осевших или испарившихся с поверхности атомов).
С учетом всех указанных выше обстоятельств, были выработаны принципы создания международной системы единиц (сокращенно СИ).
Система СИ состоит из трех групп единиц:
– основные единицы (их меньше всего) устанавливаются независимо друг от друга;
- производные единицы (получаются из основных по специальным правилам);
- кратные и дольные единицы (получаются из основных и производных по специальным правилам).
Единицы величин СИ введены в России ГОСТ 8.417-2002 [5] и подлежат обязательному применению. Ниже рассмотрим основные положения [5].
2.2 ОСНОВНЫЕ ЕДИНИЦЫ СИ
Ниже приведена таблица основных величин системы СИ.
Таблица 1 – Основные единицы СИ
| Наименова-ние физической величины | Единица | Определение | |
| Наименова- ние | Обозначение | ||
| Длина | метр | м | Метр – длина пути, проходимого светом за интервал времени 1/299792456 с |
| Масса | килограмм | кг | Килограмм – масса международного прототипа килограмма |
| Время | секунда | с | Секунда – время, равное 9192631770 периодам излучения цезия-133 |
| Электрическ-ий ток | ампер | А | Ампер – сила тока, проходящего по двум параллельным проводникам, расположенным на расстоянии 1 м и создающего силу взаимодействия, равную 2·10-7 Н |
| Температура | кельвин | К | Кельвин – единица, равная 1/273,16 точки температуры тройной воды |
| Количество вещества | моль | моль | Моль – количество вещества, содержащего столько атомов или молекул, сколько их содержится в 0,012 кг углерода |
| Сила света | кандела | кд | Кандела – сила света монохроматического излучения, энергия которой составляет 1/683 Вт/ср |
Пояснения к таблице:
1. Наименования единиц, образованные от фамилий ученых, пишутся с заглавной буквы (А; К; Н – ньютон, его размерность будет дана ниже).
2. Допускается вместо температуры в кельвинах (К) записывать значения температуры в градусах Цельсия (0 С), причем 1 К = 10 С.
3. Вт – объяснение будет дано ниже; ср – стерадиан (единица пространственного угла).
2.3 ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИ
Производные единицы образуются подстановкой основных единиц СИ в уравнения связи между величинами, вводимые по определению или в соответствии с точно установленными физическими законами.
Приведем примеры получения производных единиц.
Единица частоты периодического процесса f по определению есть величина, обратная периоду Т процесса:
f = 1 / T .
В соответствии с формулой размерность [ f ] будет:
[ f ] = 1 / [T ] = 1 / c = 1 c-1 = 1 Гц.
Герц (Гц) – специальное название единицы частоты периодического процесса, который равен количеству периодов процесса за 1 секунду.
Единицу скорости образуют с помощью уравнения, определяющего скорость прямолинейно и равномерно движущейся материальной точки
V = S / T ,
где V — скорость; S — длина пройденного пути; T — время движения материальной точки.
Подстановка вместо физических величин обозначений их единиц СИ дает
[V] = [S] / [T] = 1 м/с.
Единица ускорения устанавливается из уравнения ускорения материальной точки, движущейся прямолинейно с постоянным ускорением: если за интервал времени ΔT скорость точки изменилась на величину ΔV, то ускорение а равно
а = ΔV / ΔT.
Поступая аналогично предыдущему, получим размерность ускорения:
[a] = [V] / [T] = [S] / ([T]·[T]) = 1 м/c2 = 1 м·с-2.
В последнем выражении учтен тот факт, что при вычитании или суммировании одной и той же физической величины размерность результата не изменяется, например [ΔT] = [T2] - [T1] = [T ].
Все вышеприведенные выражения размерностей получены из формул, введенных по определению. А теперь используем физический закон – второй закон Ньютона для определения размерности силы F:
F = m·a,
где m – масса тела, кг;
а – ускорение тела, к которому приложена сила.
Опуская промежуточные вычисления, запишем окончательное выражение размерности силы:
[F] = 1 кг·м·с-2.
Размерность силы имеет специальное название – ньютон (сокращенно – Н): [F] = 1 кг·м·с-2 = 1 Н.
Продолжая ту же логику, получим размерность работы А (произведение силы на пройденный телом путь) и энергии P (их размерности совпадают, поскольку энергия системы есть ее способность совершить работу):
[A] = [F]·[L] = 1 Н·м.
Размерность работы (энергии) имеет специальное название – джоуль (сокращенно – Дж):
[A] = 1 Н·м = 1 Дж.
Следующая важная величина – мощность W (работа, совершаемая в единицу времени); единица имеет специальное наименование – ватт (Вт):
[W] = 1 Дж/c = 1 Вт.
Теперь можно перейти к определению размерности электрических величин. Напоминаем, что из основных единиц СИ только одна относится к электрическим параметрам – единица силы тока ампер (А). Чтобы связать электрические параметры с механическими, обеспечивая когерентность системы единиц, воспользуемся выражением электрической мощности постоянного тока WЭ:
WЭ = U·I,
где U – электрическое напряжение;
I – электрический ток.
Учтем тот факт, что мощность есть физическая величина, не зависящая от источника ее возникновения – механическая (например, энергия сжатой пружины); химическая (например, энергия окисления в процессе горения топлива); электрическая (например, энергия нагрева проволоки при протекании через нее электрического тока) и т.д. Это означает, что энергия любого вида, реализованная в единицу времени, имеет одинаковую размерность – Вт.
Следовательно [WЭ] = [W] и
[W] = [U]·[I], откуда [U] = [W]/ [I] = 1 Вт / A.
Единица электрического напряжения [U] имеет специальное название – вольт (сокращенно – В):
[U] = 1 Вт / A = 1 В.
Теперь, используя закон Ома, получим размерность электрического сопротивления:
R = U / I; [R] = [U]/ [I] = 1 Вт / A2 = 1 Ом.
Мы не будем далее подробно заниматься получением размерностей других производных величин (их сотни). Главное - понять логику действий для их получения: выбирается уравнение, в которое по определению или из физического закона входят основные и производные единицы уже выраженные через основные; через известные единицы выражают новую производную единицу.
Приведем в заключение две важные единицы, полученные по определению.
Первая – единица давления Р (имеет специальное название – паскаль, сокращенно – Па). Получается она как отношение силы, действующей на единичную площадь:
[P] = [F] / [L2] = 1 Н /м2 = 1 Па.
Вторая – единица плотности вещества ρ, получается как отношение единицы массы (1 кг) к занимаемому объему (м3); окончательно:
[ρ] = [m] / [L3] = 1 кг/м3.
2.4 КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ СИ
Кратные и дольные единицы образуются из основной или производной единицы умножением (делением – для дольных единиц) на целое число. Наиболее употребительными являются числа 10 в степени положительной или отрицательной и число 60 (для времени: минута – 60 секунд; час – 60 минут).
При написании кратных и дольных единиц используется два способа:
- написание десятичного множителя перед размерностью величины, например, 103 с; 10-2 К; 106 Ом;
- дополнением размерности специальными приставками (мега, кило, милли и т.д.).
Ниже будет приведена таблица соответствия между первым и вторым вариантом записи кратных и дольных величин. Но предварительно сделаем два замечания.
Первое. Необходимо твердо усвоить, что кратные единицы, начиная с 106 и более пишутся с заглавной буквы, а дольные – всегда с прописной. Например, 1 МОм – один миллион Ом, а 1 мОм – одна тысячная доля Ома.
Второе. Исторически сложилось наименование единицы массы с приставкой «кило» - 1 кг, а тысячная доля единицы не имеет приставки – 1 г.
Таблица 2 – Множители и приставки, используемые для образования наименований и обозначений кратных и дольных единиц СИ
| Десятичный множитель | Приставка | Обозначение приставки | Десятичный множитель | Приставка | Обозначение приставки |
| 1018 | иотта | И | 10-1 | деци | д |
| 1015 | пета | П | 10-2 | санти | с |
| 1012 | тера | Т | 10-3 | милли | м |
| 109 | гига | Г | 10-6 | микро | мк |
| 106 | мега | М | 10-9 | нано | н |
| 103 | кило | к | 10-12 | пико | п |
| 102 | гекто | г | 10-15 | фемто | ф |
| 101 | дека | да | 10-18 | атто | а |
Приведем несколько примеров применения кратных и дольных величин.
Сопротивление изоляции провода R составляет 5,3 миллиона Ом
R = 5,3·106 Ом = 5,3 МОм,
а сопротивление самого провода r – 120 тысячных долей Ом:
r = 120·10-3 Ом = 120 мОм.
Емкость конденсатора С равна 120 миллионных долей фарады (сокращенное название единицы – Ф)
С = 120·10-6 Ф = 120 мкФ.
3 ПОГРЕШНОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
3.1 ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Ранее было указано, что модели физических величин, подлежащих измерению, приблизительно соответствуют самой величине. А в измерительных приборах эталоны единиц физических единиц заменяются более грубыми устройствами, называемыми мерами. Другие устройства, обеспечивающие получение числового значения физической величины (устройства масштабирования, сравнения и т.д.) так же не идеальны.
Как следствие, численное значение результата измерений y будет отличаться от значения x, которое было бы получено при идеальных характеристиках всех элементов измерителя и идеально точной модели измеряемой величины x.
Разность между результатом измерений y и истинным значением физической величины x называется абсолютной погрешностью измерений Δ [3]:
Δ = y – x. (3.1)
Поскольку истинное значение измеряемой величины неизвестно, то в расчетах вместо нее используется действительное значение, которое получают, измеряя ту же величину измерительным устройством с меньшей погрешностью (обычно в 3-10 раз).
Иногда вместо термина «погрешность» применяют термин «точность», под которым понимают величину обратную погрешности. В любом случае для вычисления точности необходимо сначала определить погрешность измерения и смысл выполнения дополнительной операции теряется. Скорее «точность» применяется для удобства речи, понимая, что чем выше точность, тем меньше погрешность.
Абсолютная погрешность измерений не полностью характеризует результат применения определенных средств измерения и методики выполнения. Действительно, погрешность в 5 г при взвешивании товара в магазине вполне приемлема, но та же погрешность при приготовлении лекарства может кончиться летальным исходом для больного.
Поэтому вводится второй вид погрешности – относительная погрешность измерений, равная отношению абсолютной погрешности Δ к результату измерений y:
γ = Δ / y. (3.2)
Абсолютная погрешность измерения – размерная величина, а относительная погрешность – величина безразмерная и выражается числом или процентами.
Важный вопрос – какую погрешность результата измерений считать допустимой. Ответ на него выходит за рамки теории измерений. Допустимая погрешность устанавливается исходя из требований измерительной задачи. Например, расход природного газа, поступающего в котельную, измеряют с относительной погрешностью до 3 %, а расход того же газа в магистральных газопроводах и нефти в нефтепроводах не превышает 0,5 %. Относительная погрешность навигационной системы GPS, позволяющей определять координаты объектов с абсолютной погрешностью не более 1 м, не превышает 1·10-9. При производстве микросхем количество примесей в используемых веществах не должно превышать 1 атом на 107 атомов основного вещества. Следовательно, относительная погрешность средств измерения химического состава газов и твердых веществ на предприятиях микроэлектроники не должна превышать значения 1·10-7.
3.2 СОСТАВЛЯЮЩИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
При выполнении измерений стремятся по возможности снизить погрешность результата. С этой целью проводят анализ источников погрешности, а потом, поняв природу их возникновения, разрабатывают методы их снижения (или учета).
По источнику возникновения погрешности делятся на методические и инструментальные. Источником методических погрешностей являются особенности метода измерений или расхождения между моделью измеряемой физической величины и самой величиной. Источником инструментальной погрешности являются несовершенство средств измерения или их нестабильность. Инструментальная погрешность будет более подробно рассмотрена в следующем разделе, а сейчас остановимся на методической погрешности.
Примеры моделей физических величин и их несоответствия истинным значениям величин приводились в п. 1.2. Рассмотрим еще один пример, который доведем до получения значения методической погрешности.
Большая часть вольтметров переменного тока предназначена для получения числовых значений действующих величин напряжений. Действующей величиной переменного напряжения называется постоянное напряжение, выделяющее на омической нагрузке такое же количество энергии, как и измеряемое переменное.
Выражение для напряжения переменного синусоидального сигнала имеет вид
 ,
,
где Um – амплитудное (максимальное) значение синусоиды;
ω = 2π /Т– круговая частота колебаний;
Т – период колебаний;
t – текущее время;
φ – начальная фаза колебаний.
Действующее напряжение Uд определяется как корень квадратный из средней мощности, выделяемой на сопротивлении в 1 Ом:
 . (3.3)
. (3.3)
При взятии интеграла учтено, что
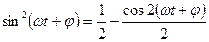 и второй интеграл в квадратных скобках равен нулю.
и второй интеграл в квадратных скобках равен нулю.
Следовательно, для измерения максимального (амплитудного) значения синусоидального сигнала нужно результат измерений Uд умножить на 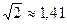 . Но если сигнал по форме отличен от синусоиды и это не учтено в модели измеряемой величины, то неизбежны методические погрешности.
. Но если сигнал по форме отличен от синусоиды и это не учтено в модели измеряемой величины, то неизбежны методические погрешности.
Для определенности будем считать, что сигнал представляет собой периодическую последовательность прямоугольных импульсов (рисунок 3.1)
 Импульсы имеют ту же амплитуду Um и период следования T, что и синусоидальный сигнал; длительность импульсов обозначена буквой τ.
Импульсы имеют ту же амплитуду Um и период следования T, что и синусоидальный сигнал; длительность импульсов обозначена буквой τ.
Определим показания вольтметра для рассматриваемого случая, подставив параметры импульсной последовательности вместо синусоиды в выражение (3.3):
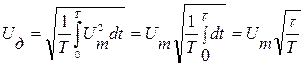 . (3.4)
. (3.4)
Рассчитаем по (3.4) показания вольтметра при отношениях τ/Т = 0,8и при τ/Т = 0,1. В первом случае Uд1 ≈ 0,9 Um, во втором - Uд2 ≈ 0,32 Um. Теперь, исходя из модели синусоидального сигнала, определим амплитуды импульсов, умножая Uд1 и Uд2 на 1,41; получим, соответственно,
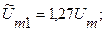
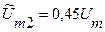 .
.
Считая абсолютные погрешности по формуле (3.1), вычислим методические погрешности измерений:
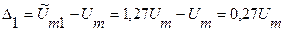 ; аналогично Δ2 = -0,55Um.
; аналогично Δ2 = -0,55Um.
Погрешности получаются очень большими и крайне редко можно встретить измерительные задачи, в которых подобная погрешность считалась бы приемлемой.
Особенно наглядно значение погрешности видно при переходе к относительной погрешности по формуле (3.2):
 , аналогично
, аналогично  .
.
Чем объясняется столь большие величины погрешностей измерений? Ответ – неадекватностью модели физической величины реальному ее виду. Следовательно, прежде чем приступать к измерениям напряжения, необходимо уточнить какова форма исследуемого сигнала, создать адекватную его модель и только после этого выбирать соответствующее средство измерений.
Разработку моделей физических величин, к сожалению, не удается формализовать; корректность модели зависит от опыта и квалификации специалистов, ее создающих. Грубые модели, как мы видели, ведут к очень большим погрешностям, а сложные подробные модели – к неоправданному усложнению измерительных средств и большим экономическим затратам на проведение измерений.
Мы рассмотрели погрешности измерений с точки зрения источников их появления (анализ инструментальных погрешностей будет проведен в другой главе). А теперь рассмотрим, как ведут себя погрешности (без уточнения источника их появления) при выполнении многократных измерений одним прибором или одновременных измерениях одной физической величины несколькими однотипными приборами.
Исследования показали, что с указанной точки зрения погрешности можно разделить на постоянные (или изменяющиеся по известному закону) и случайные. Постоянная составляющая погрешности называется систематической погрешностью, а изменяющаяся часть называется случайной погрешностью.
Источниками систематической погрешности могут быть: отложения твердых частиц на стенке трубы расходомера, что уменьшает ее диаметр; попадание загрязнений или пылинок на чашку весов; трение в осях поворотных устройств (передаточных шестерней, стрелочных указателей и т.д.); воздействие электромагнитных полей от мощных потребителей (электродвигателей, нагревательных печей); воздействие на измерительный прибор внутренних и внешних источников тепла.
Случайные погрешности отличаются тем, что их нельзя предсказать ни по величине, ни по знаку в отдельно взятом измерении. Источниками их могут быть собственные шумы электронных схем измерительных приборов; внешние переменные температурные или электромагнитные поля (например, от сварочных аппаратов, мощных переключателей); изменения напряжения питания прибора или температурных режимов отдельных элементов.
Совершенно естественно, что, описывая объекты материального мира в виде чисел, сами измерительные устройства, процедуры измерений и результат измерений подвергаются математическому анализу. В частности, для анализа погрешностей используется аппарат теории вероятности и математической статистики. Это большой раздел математики, дающий колоссальные возможности для анализа случайных величин и процессов. Но мы кратко рассмотрим только необходимые для понимания дальнейшего материала минимальные сведения.
3.3 ВВЕДЕНИЕ В ТЕОРИЮ ВЕРОЯТНОСТЕЙ
3.3.1 Вероятности событий
Теория вероятностей и математическая статистика рассматривают случайные события. Под случайным событием понимается любое событие, которое может произойти или не произойти в процессе наблюдения. Примеры: самолет может прилететь по расписанию, а может и задержаться; устройство измерений может быть исправно или нет в момент его проверки; урожай зерновых может быть больше прошлогоднего, а может быть и меньше (или таким же); день может быть солнечным или пасмурным и т.д.
Обычно случайные события рассматриваются в некоторой взаимосвязи. Например, для получения достоверных измерений необходимо, чтобы были исправны все измерительные устройства (случайные события), исправны источники электропитания и компьютер, управляющий работой измерительных устройств. Чтобы рассмотреть совместно разнородные события необходимо ввести для них единую меру. Такой мерой является вероятность события.
Под вероятностью события А понимается предел, к которому стремится отношение числа n благоприятных исходов опытов к их общему числу N при стремлении N к бесконечности.
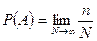 . (3.5)
. (3.5)
Очевидно, что число благоприятных исходов для разных ситуаций может быть разным. Например, если проводить эксперименты по самопроизвольному взлету кирпича с земли на 5 этаж, то при любом числе экспериментов n = 0. И вероятность такого события равна 0. Такое событие называется невозможным событием. А если каменщик случайно роняет кирпичи, то при любом N число падений кирпича на землю n = N. Вероятность такого события равна 1 и оно называется достоверным событием. Все возможные события располагаются от невозможного до достоверного.
Из сказанного можно сделать два вывода.
Во – первых, теория вероятности оперирует только большим количеством событий. Уникальное явление не может быть проанализировано методами теории вероятности. Например, отказ одного средства измерений ничего не говорит о надежности других устройств; измеренный рост одного человека не характеризует рост остальных жителей России и т.д.
Во – вторых, мерой случайного события является вероятность его появления, которая принимает значения в интервале от 0 до 1:
0 ≤ Р ≤ 1. (3.6)
3.3.2 Несовместные события
Если события А, В, С могут появляться при проведении N наблюдений, но никогда не появляются одновременно в одном наблюдении, подобные события называются несовместными.
Поясним сказанное примером. Допустим, на артиллерийском орудии установлена дальность стрельбы 2 км. По многим причинам (направление и сила ветра; погрешность в массе пороха; погрешность в массе и форме снаряда) точки падения снарядов рассеиваются в области примерно удаленного от орудия на 2 км. Под событием А будем понимать попадание снарядов в окружность радиусом 10 м вокруг точки теоретического попадания (2 км); под событием В – попадание в кольцо, ограниченное радиусами от 10 до 20 м; событие С - попадание в кольцо, радиусами от 20 м до 40 м.
Если из N = 100 выпущенных снарядов n1 = 10 попало в окружность, радиусом 10 м, то будем считать, что 10 раз реализовалось событие А; вероятность его Р (А) = 0,1. Аналогично, если в первое кольцо (событие В) попало n2 = 20 снарядов из 100, то Р(В) = 0,2; во второе кольцо (событие С) попало n3 = 40 снарядов, то Р(С) = 0,4. Совершенно очевидно, что снаряды, упавшие в пределах окружности, не могут принадлежать одновременно кольцу и наоборот. Следовательно, события «попадание в окружность; попадание в первое кольцо; попадание во второе кольцо» являются несовместными.
Если по поражающей способности снаряда удовлетворительным считается попадание в окружность, радиуса 40 м, то события А, В и С являются благоприятными исходами стрельбы. Вопрос: чему равна вероятность попадания снаряда, если вероятности событий А, В и С известны?
Считаем по формуле (3.5):
Р(А или В или С) = (n1 + n2 + n3) / N = n1/ N + n2 / N + n3 / N =
= Р(А) + Р (В) + Р(С) = 0,1 + 0,2 + 0,4 = 0,7.
Полученный результат означает, что вероятность поразить цель одним выстрелом составляет 0,7, а с вероятностью 0,3 может иметь место промах.
Условно логическое сложение (А или В или …) заменяют знаками суммы (при этом необходимо помнить, что события не суммируются в арифметическом смысле, поскольку это не числа). При этом последнее выражение приобретает вид:
Р(А + В + С) = Р(А) + Р(В) + Р(С). (3.7)
То есть: вероятность суммы независимых событий равна сумме вероятностей этих событий. А поскольку вероятности обычные числа, то над ними можно производить любые математические операции.
И последнее: если к вероятности попадания прибавить вероятность промаха (два несовместных события), то общая вероятность будет равна единице. Сумма событий, общая вероятность которых равна 1, называется полной группой событий.
3.3.3 Независимые события
Независимыми событиямиА и В называются события, наблюдаемые в одном эксперименте, но вероятности появления которых не зависят друг от друга. Например, событие А – работоспособность измерительной части прибора с вероятностью Р(А); событие В – работоспособность блока питания того же прибора с вероятностью Р(В). Понятно, что получить результат измерения можно только в том случае, когда работоспособна измерительная часть прибора и блок питания. Выход из строя любой части ведет к невозможности получения результатов измерений.
Как определить вероятность безотказной работы прибора, если известны вероятности Р(А) и Р(В)?
Ответ (доказательства можно посмотреть в любом учебнике по теории вероятности):
Р(события А и события В) = Р(А)·Р(В).
Условно совместное появление событий А и В обозначают знаком умножения (еще раз напоминаем, что производить арифметические действия с событиями невозможно) и последнее выражение записывается в виде
Р(А·В) = Р(А)·Р(В). (3.8)
Если в рассмотренном примере считать вероятность безотказной работы измерительной части прибора Р(А) = 0,8, а блока питания Р(В) = 0,9, то вероятность безотказной работы всего прибора будет равна
Р(А·В) = 0,8 ·0,9 = 0,72.
Интуитивно понятно, что более сложное устройство с большим числом элементов менее надежно, чем простое. Но придание надежности числового выражения в виде вероятности безотказной работы принципиально изменяет ситуацию. Числовые оценки надежности позволяют, во – первых, сравнивать надежность устройств одного назначения, выполненных по разным технологиям или схемам и, во – вторых, разрабатывать конструкции надежных устройств из ненадежных элементов.
3.3.4 Сумма совместных независимых событий
Рассмотрим события А и В, которые могут появляться в одном наблюдении, а может одно (или оба) не появляться. Например, измерительный медицинский комплекс, используемый во время хирургических операций, питается от двух независимых источников электропитания. При этом возможны ситуации, когда исправны оба источника (реализуется события А и В), исправлен первый источник (событие А) и неисправен второй; исправен второй источник (событие В) и неисправен первый; оба источника питания неисправны.
Благоприятными для завершения операции можно считать первые три ситуации, когда хотя бы один источник питания обеспечивает работу системы измерений. Вероятность такого события равна:
Р(А + В) = Р(А) + Р(В) – Р(А)·Р(В). (3.9)
Если оба источника имеют равную вероятность безотказной работы, например, Р(А) = Р(В) = 0,8, то вероятность совместного события
Р(А + В) = 0,8 + 0,8 – 0,8 ·0,8 = 0,96.
Вероятность безотказной работы системы питания при использовании двух источников повысилась; вот один из методов повышения надежности технических устройств.
3.3.5 Дискретные законы распределения и обобщенные характеристики
Среди случайных событий есть класс событий, выражаемых числами. Называются они случайными величинами. Например, урожайность, удои, возраст жителей, скорости молекул газа, погрешности измерений, прибыли банков и т.д.
Замечательная особенность случайных величин Х заключается в том, что каждой величине может быть сопоставлена вероятность ее появления. Таким образом, зависимость вероятностей появления случайных чисел представляется в виде функции Р(Х), которую можно подвергнуть анализу. Функция Р(Х) называется законом распределения случайной величины Х. Под заглавными буквами X, Y будем понимать совокупность различных случайных величин. Например X – количество расходомеров в n котельных одного района; Y – количество работников котельных того же района. Прописными буквами x, y будем обозначать конкретное значение случайной величины. Например, в первой котельной 10 расходомеров, а во второй – 6, следовательно, x1 = 10, x2 = 6.
Случайные величины делятся на дискретные и непрерывные. К дискретным случайным величинам относятся те, которые принимают на числовой оси отдельные значения, например, число посещений больницы жителями района за год, количество отказавших приборов за определенный интервал времени, количество деревьев на одном гектаре леса и т.п. К непрерывным случайным величинам относятся те, которые могут принимать любые значения на числовой оси или ее части. Например, погрешности измерений, скорости молекул, температура в сушильном аппарате, давление пара перед турбиной и т.д.
Сначала рассмотрим дискретные величины. Зависимость вероятности появления случайной величины от ее значения Р(Х) может быть записана в аналитическом виде, в виде таблицы или графика.
Например, рассмотрим следующую типичную задачу. При изготовлении деталей вероятность получения годной детали равна р = 0,6 и, соответственно, вероятность получения бракованного изделия равна q = 0,4 (поскольку получение годной или бракованной детали образуют полную группу событий). Для контроля качества технологического процесса отбирают 8 деталей. Определить вероятность наличия среди отобранных деталей: ни одного бракованного, ровно 1 бракованного, 2 бракованных и т.д. до 8.
Аналитическое выражение числа бракованных деталей дается в общем виде биномиальным законом распределения:
 , (3.10)
, (3.10)
где pk – вероятность появления в отобранной партии из n деталей ровно k бракованных;
 - сочетание из n элементов по k;
- сочетание из n элементов по k;
n!,k! – факториалы соответствующих значений n и k; напоминаем, что 0! = 1.
Рассчитаем вероятность отсутствия бракованных деталей в партии из 8 штук. По формуле (3.10) при n = 8 и k = 0 имеем:
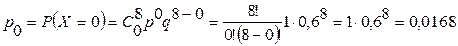 .
.
Для случая ровно одной бракованной детали по той же формуле получим:
 .
.
Продолжая расчет для случаев k = 2, 3, …8 получим значения вероятностей, отвечающих каждому возможному числу бракованных деталей. Результаты сведем в таблицу, которая будет табличной формой представления закона распределения случайного числа бракованных деталей в партии из 8 штук:
| k | |||||||||
| pk | 0,0167 | 0,0895 | 0,209 | 0,279 | 0,232 | 0,124 | 0,0412 | 0,008 | 0,0006 |
По данным таблицы можно закон распределения представить в графической форме (рисунок 3.2).

Понятно, что все формы представления закона распределения случайной величины равноценны и выбор конкретной формы определяется удобством дальнейшего анализа.
Данные таблицы и графика наглядно показывают достаточность выборки из 8 деталей для анализа стабильности технологического процесса производства детали. Вероятность появления 8 исправных деталей при наличии брака не превышают величины 0,0167, а остановка производства по причине выпуска только бракованных деталей вообще крайне мала (0,0006).
Хотя законы распределения дают максимум информации о случайных величинах, их использование очень неудобно. Это ясно видно в случаях большого количества значений случайной величины. Например,
Дата добавления: 2015-01-29; просмотров: 232; Мы поможем в написании вашей работы!; Нарушение авторских прав |