Про обозначения

К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ù,Ú,), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù, Ú,), что еще раз подчеркивает проблему. Далее во всех решениях приводятся два варианта записи.

Что нужно знать:

· условные обозначения логических операций

A, не A (отрицание, инверсия)

A Ù B, A и B (логическое умножение, конъюнкция)

A Ú B, A или B (логическое сложение, дизъюнкция)

A→B импликация (следование)

· таблицы истинности логических операций «И», «ИЛИ», «НЕ», «импликация» (см. презентацию «Логика»)

· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:

A→B = A Ú Bили в других обозначениях A→B =

· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация»

· иногда полезны формулы де Моргана[1]:

(A Ù B) = A Ú B

(A Ú B) = A Ù B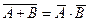

Пример задания:

Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {2, 4, 6, 8, 10, 12}) → (((x Î {4, 8, 12, 116}) Ù (x Î A)) → (x Î {2, 4, 6, 8, 10, 12}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

Решение:

1) Заметим, что в задаче, кроме множества A, используются еще два множества:

P = {2, 4, 6, 8, 10, 12} Q = {4, 8, 12, 116}

2) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

3) перейдем к более простым обозначениям

4) раскрываем обе импликации по формуле :

5) теперь используем закон де Моргана :

6) поскольку это выражение должно быть равно 1, то A должно быть истинным везде, где ложно

7) тогда минимальное допустимое множество A – это (по закону де Моргана)

8) переходим ко множествам

– все натуральные числа, кроме {4, 8, 12, 116}

– все натуральные числа, кроме {2, 4, 6, 8, 10, 12}

9) тогда – это все натуральные числа, которые входят одновременно в и ; они выделены жёлтым цветом: {4, 8, 12}

10) именно эти числа и должны быть «перекрыть» множеством А_min, поэтому минимальный состав множества A – это А_min = {4, 8, 12}, сумма этих чисел равна 24

11) Ответ: 24.

Пример задания:

На числовой прямой даны два отрезка: P = [37; 60] и Q = [40; 77]. Укажите наименьшую возможную длину такого отрезка A, что формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Решение:

12) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

13) перейдем к более простым обозначениям

14) раскрываем обе импликации по формуле :

15) теперь используем закон де Моргана :

16) в таком виде выражение уже смотрится совсем не страшно; Сразу видно, что отрезок должен перекрыть область на числовой оси, которая не входит в область :

17) по рисунку видно, что не перекрыт только отрезок [40;60] (он выделен жёлтым цветом), его длина – 20, это и есть правильный ответ.

18) Ответ: 20.

Ещё пример задания:

На числовой прямой даны два отрезка: P = [10,39] и Q = [23, 58]. Выберите из предложенных вариантов такой отрезок A, что логическое выражение

((x Î P) Ù (x Î A) ) → ((x Î Q) Ù (x Î A) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [5, 20] 2) [15, 35] 3) [25, 45] 4) [5, 65]

Решение:

1) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

2) перейдем к более простым обозначениям