СУ-определение.

СУ-определение – это обобщение КС грамматики в которой каждый грамматический символ имеет связанное с ним множество атрибутов, разделенное на два подмножества: синтезируемые и наследуемые атрибуты этого грамматического символа.

Атрибут может представлять собой все, что угодно – строку, число, тип, адрес памяти и т.д.

Значение атрибута в узде дерева разбора определяется семантическими правилами, связанной с используемой в данном узле продукцией.

Значение синтезируемого атрибута в узле вычисляется по значениям атрибутов, в дочерних узлах по отношению к данному узлу.

Значение наследуемого атрибута определяется значением атрибутов соседних (т.е. узлов, дочерних по отношению к родительскому узлу данного) и родительских узлов.

Семантические правила определяют зависимость между атрибутами. Эта зависимость определяется графом.

Граф зависимости определяет порядок выполнения семантических правил, что дает значение атрибутов в узлах дерева разбора входной строки.

Естественно необязательно строить в явном виде дерево и граф. Главное, чтобы для каждой входной строки выполнялись верные действия в правильном порядке.

В СУ-определении каждая продукция грамматики типа имеет связанное с ней множество семантических правил вида: 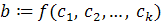, здесь f – функция, - атрибуты грамматических символов продукции, b – синтезируемый атрибут символа a или наследуемый атрибут одного из грамматических символов правой части продукции.

Пример 1. Построить СУ-определение настольного калькулятора.

Оно связывает с каждым из нетерминалов целочисленный атрибут val. Для каждой продукции семантическое правило вычисляет значение val нетерминала левой части по значению атрибутов нетерминалов правой части.

Продукция

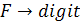
Семантическое правило

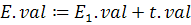
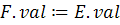
n – символ новой строки, lex.лучение цифры значения в лексическом анализе.

Например, получив в качестве строки 3*5+4 n выводится 19.

Дерево будет выглядеть следующим образом.

Пример 2. Наследуемые атрибуты.

Продукция.

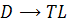
Семантическое правило.

L.in:=T.type

T.type:=integer

T.type:= real

Addtype(id.entry, L.in)

Это таблица с наследуемым атрибутом L.in

Теперь будем строить для real id1, id2, id3 дерево разбора с наследуемым атрибутом in в каждом узле, помеченном нетерминалом L.

Значения L.in в трех узлах дает тип идентификаторов id1, id2, id3. Эти значения определяются вычислением значения T.type в левом дочернем по отношению к корню узле, а затем вычислением L.in в нисходящем порядке в трех L узлах правого поддерева корневого узла.

В каждом L узле мы выдаем процедуру L.type для записи в таблицу символов, информация о том, что идентификатор в правом дочернем узле имеет тип real.